The problem to be solved is to find stationary space distribution of
stars which have had certain initial space and velocity distributions and
move in a given potential. The potential is supposed to be axially
symmetric, constant in time and not affected by this stellar population.
In principle, the most straightforward way to obtain the solution is
to integrate directly the equations of motion for a sufficiently
large number of stars with different initial conditions. This method
was indeed used in the Paczynsky (1990) and Hartmann et al. (1990) papers.
Here we propose to use another method based
on finding the solution of collisionless Boltzmann equation.
Define 
be a distribution function of stars in 6-dimensional phase space. Then
space density is given by 
.
Time evolution of the distribution function is generally described by
the kinetic equation
where 
is the potential.
Axial symmetry implies that only two
cylindrical coordinates r and z are required. In the case considered
the problem can be significantly simplified because at least two integrals
of motion exist - the full energy E and angular momentum along the z-axis
(here and below we consider all stars of unit mass):
with 
being absolute value of the initial velocity,
and 
- circular velocity. So the problem can be reformulated as follows:
from a given distribution function 
(that is, the number of
stars with energy in between E and E+dE and angular momentum
in between and 
) in 2-dimensional space
to find the distribution function in 6-dimensional
phase space.
As we are interested in investigation of old neutron star
distribution, we can safely get rid off time dependence
and search for equilibrium solution of the collisionless
equation.
Conservation of full number of stars gives rise to the relation
Introduce cylindrical space coordinates
r, z, 
and spherical coordinates
, 
, 
in the velocity space.
The direction of can be
chosen arbitrary, say along orbital velocity 
,
being the angle between 
and and - azimuthal angle.
Then make transformation in the velocity space from the introduced
spherical coordinates to coordinates 
. Using (1) calculate
Jacobian 
of the
transform 
. Finally we
obtain for Q
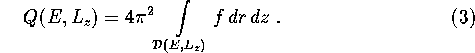
Here 
denotes the region in r, z-space where the
motion is allowed with the given angular momentum and energy 
.
Now assume that the motion in the chosen potential is ergodic, or
equivalently, that a test particle moving long enough in this potential
will sweep uniformly the hypersurface of constant in
the phase space 
. Then the distribution function
f in equation (3) can be treated as constant and is obtained directly
from (3) provided is known. The density Q can be found
straightforwardly from the initial distributions p(r,z) and 
using the same equation (3)
with 
(note that is
expressed through 
, which follows from statistical calculations,
and 
; see below).
Finally, we obtain as a solution
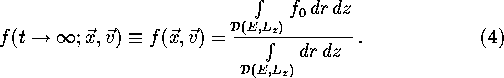
Basically this result is an equivalent formulation of the ergodic hypothesis. The latter should be proved for each potential separately, because no general theorem exists for axisymmetrical potentials. We will briefly discuss this problem below.