<< 7.2 Усилители импульсного сигнала | Оглавление | 7.4 Подготовка к наблюдениям >>

7.3 Счетчики импульсов и метод накопления

Усиленные и сформированные импульсы по коаксиальному кабелю длиной около 10 м поступают на счетчики. Счетчики установлены в корпусе микроЭВМ ``Электроника-60'', являющейся ядром управляющей и регистрирующей части комплекса. Счетчики обеспечивают максимальную скорость счета около 80 МГц. С точки зрения процессора ЭВМ счетчики являются внешним устройством машины, и, как всякое внешнее устройство, имеют регистр управления и регистры данных. Кроме импульсов от усилителей, на платы счетчиков поступают данные от датчика времени, в качестве которого применяется синхронометр (электронные часы) типа Ч7-15. Импульсы от синхронометра позволяют точно задавать интервал времени накопления. В нужный момент с этого же синхронометра в память ЭВМ вводится абсолютное значение времени.

Пусть за единичный интервал времени $\Delta t$ на вход счетчика поступило импульсов, причем требуется чтобы относительная статистическая погрешность вашего измерения не превышала некоторого числа $\varepsilon$ . Квантовые флуктуации светового потока подчиняются распределению Пуассона, согласно которому дисперсия измеренного количества импульсов $\sigma^2=n$ , среднеквадратическое уклонение $\sigma=\sqrt{n}$ , а относительная среднеквадратическая ошибка $\varepsilon = \sigma/n$ . Следовательно, чтобы иметь относительную ошибку менее 1% необходимо накопить $N(\varepsilon)\ge10^4$ импульсов, менее 0.5% - $N(\varepsilon)\geq4\cdot 10^4$ , и менее 0.1% - $N(\varepsilon)\geq10^6$ импульсов. Время накопления , необходимое для получения относительной ошибки не более чем $\varepsilon$ , равно $N(\varepsilon)/n$ .

Кроме квантовых флуктуаций, световой поток от звезды флуктуирует за счет атмосферных мерцаний. Процесс мерцаний имеет широкий частотный спектр. Наиболее характерные частоты заключены в интервале от 10 до 100 Гц, однако имеется и низкочастотная составляющая мерцаний с характерными частотами до 0.1 Гц. В связи с этим даже при очень больших световых потоках не следует применять экспозиции меньшие чем $\approx10$ с. Оба эти процесса: квантовые флуктуации и мерцания влияют на величину средней квадратической ошибки $\sigma$ среднего значения количества импульсов за принятое время экспозиции, которое определяется по обычной формуле:

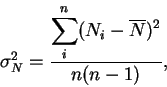
$\begin{displaymath} {\sigma}_N^2=\frac{\displaystyle\sum\limits_{i}^{n} (N_i-{\overline{N}})^2}{n(n-1)}, \end{displaymath}$

где

-- число измерений,

-- результаты индивидуальных измерений, а $\overline{N}$ -- среднее количество импульсов за одно измерение. Удобно, если ваша аппаратура в процессе накопления в каждый момент будет ``знать'' чему равна относительная среднеквадратическая ошибка $\varepsilon = \sqrt{\sigma^2_N}~:~{\overline N}$ и завершит процесс по достижении заданной точности. Для этого нужно накапливать сигнал сериями из малых интервалов времени. Аппаратура Тянь-Шаньской обсерватории позволяет изменять длительность таких малых интервалов от 1 миллисекунды до единиц секунд. Стандартной длительностью единичного акта накопления считается 20 мс.

Пусть теперь вы накопили сигнал несколько раз по 20 мс. Это ``несколько'' должно быть ``довольно много'', чтобы уверенно определить среднее и относительную среднеквадратическую ошибку. В нашем случае ``довольно много'' равно 64. Если после накопления первых 64 чисел за первые 64 временных интервала по 20 мс заданная точность не достигнута, то нужно накопить еще 64 числа, и так далее. Когда относительная среднеквадратическая ошибка по всем четырем каналам станет меньше наперед заданных значений, накопление нужно закончить. Такой алгоритм реализован в программе управления процессом накопления. При слабых сигналах (например от фона неба) бывает так, что за разумное время невозможно достичь заданной величины относительной ошибки. Тогда, естественно, поставить какое-то ограничение по времени. В стандартном варианте оно составляет 30 с.

<< 7.2 Усилители импульсного сигнала | Оглавление | 7.4 Подготовка к наблюдениям >>