The most precisely determined characteristic for accreting neutron stars (NS's) is their period. Thus using observations of the period we can determine different properties of the observed object.
Period changes show fluctuations. These fluctuations were discussed in
de Kool ![]() Anzer (1993). The authors determined noise level in these systems
and characteristic time scales. Using these results we can estimate diffusion
coefficients in the Fokker-Planck equation (see below)
and the stellar wind velocities (only for the wind-accreting systems ).
Anzer (1993). The authors determined noise level in these systems
and characteristic time scales. Using these results we can estimate diffusion
coefficients in the Fokker-Planck equation (see below)
and the stellar wind velocities (only for the wind-accreting systems ).
During accretion the angular momentum of plasma is transfered to the NS. But the process of the momentum transfer is not stationary. The transfered angular momentum fluctuates and therefore the period changes of the NS will also show fluctuations.
Processes with fluctuations are well known (see for example Haken (1978)).
Some applications
of stochastic processes in astrophysics especially in accreting systems
were discussed in Lipunov (1987),Hoshino ![]() Takeshima (1993)
and Lipunov (1992).In Hoshino
Takeshima (1993)
and Lipunov (1992).In Hoshino ![]() Takeshima (1993) the authors,
using simple models of MHD
turbulence, try to explain aperiodic changes in X-ray luminosity of
X-ray pulsars. Luminosity fluctuations are explained as the result of
density fluctuations due to turbulence in the plasma flow.
The authors used 2D model for accretion disk and 3d model
for the wind accreting
systems. Detailed exploration of this question is very difficult in both:
theoretical and observational ways (there is no good theory of MHD turbulence
and the resolution of modern equipment of satellites is not high enough for
power spectra of X-ray pulsars (see Hoshina
Takeshima (1993) the authors,
using simple models of MHD
turbulence, try to explain aperiodic changes in X-ray luminosity of
X-ray pulsars. Luminosity fluctuations are explained as the result of
density fluctuations due to turbulence in the plasma flow.
The authors used 2D model for accretion disk and 3d model
for the wind accreting
systems. Detailed exploration of this question is very difficult in both:
theoretical and observational ways (there is no good theory of MHD turbulence
and the resolution of modern equipment of satellites is not high enough for
power spectra of X-ray pulsars (see Hoshina ![]() Takeshima 1993).
But detailed exploration
of the density fluctuations will help to understand period fluctuations. It
will be very interesting to compare X-ray luminosity fluctuations with
fluctuations of the period of the NS.
Takeshima 1993).
But detailed exploration
of the density fluctuations will help to understand period fluctuations. It
will be very interesting to compare X-ray luminosity fluctuations with
fluctuations of the period of the NS.
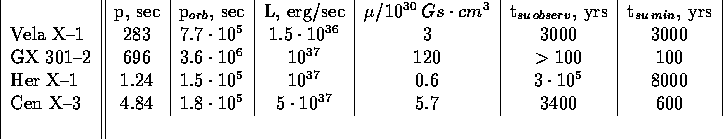
Table 1:
There are different methods of describing of these processes. In this work we use differential equations for the distribution function. For the frequency changes we can write the Langeven equation, which describes the process with fluctuations:
![]()
Here, ![]() -constant angular momentum. For
-constant angular momentum. For ![]() in
the most general form we can write (Lipunov 1982):
in
the most general form we can write (Lipunov 1982):
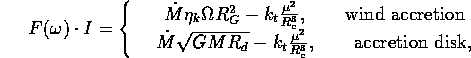
where -disk radius, and -dimensionless parameters (), I-moment of inertia of the NS, M- mass of the NS, -orbital frequency of the system, - radius of gravitational capture (, we include here the orbital velocity) and -corotational radius, .
We assume that the 'force' is conservative and in this case we can write
![]() in the form:
, where V is a scalar potential.
is a fluctuating moment, i.e. , (Lipunov 1987).
in the form:
, where V is a scalar potential.
is a fluctuating moment, i.e. , (Lipunov 1987).
The distribution of frequency, , is described by the distribution function . This function satisfies the Fokker-Planck equation (Haken 1978):
![]()
where D is the 'diffusion coefficient', which is determined by the correlation of the stochastic force :
![]()
Stationary solution of the eq.(2) is the following:
![]()
where N is determined from the normalisation condition:
![]()
Using expression for from Lipunov (1992) we can write D in the form:
![]()
where -constant parameter , I-moment of inertia of the NS and is evaluated as , here -time of spin-up and -the characteristic time for period changes (see for details Lipunov (1987) or Lipunov (1992)).
Using eq.(6) in 2.1 we shall determine the value of the 'diffusion coefficient', D. With these D in 2.2 we shall make the estimates of the stellar wind velocities for Vela X-1 and GX 301-2.