Under the assumptions made above, we can calculate
the binary merging rates in the Galaxy R. The results are
presented in Fig. ![]() and
and ![]() .
.
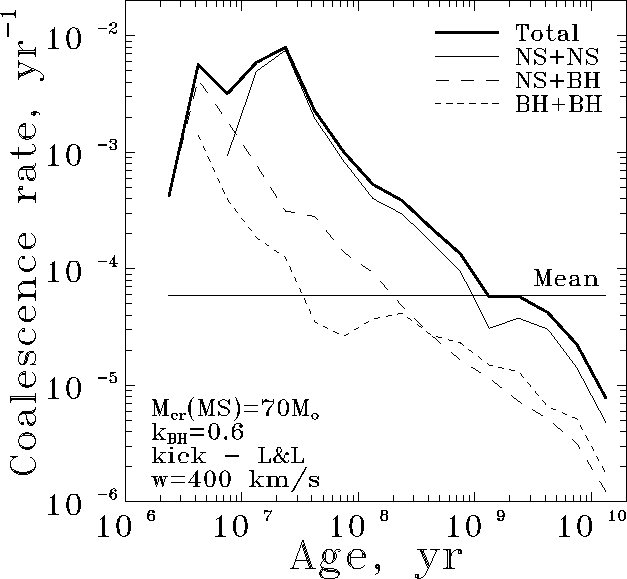
Figure: The dependence of different compact binary
merging rates in a model ``elliptical'' galaxy
(where all the stars were formed simultaneously
at the moment t=0) with mass ![]() M
M ![]() .
The horizontal line shows the mean merging rate of binary NS
in a spiral galaxy of the same mass with a stationary star formation.
.
The horizontal line shows the mean merging rate of binary NS
in a spiral galaxy of the same mass with a stationary star formation.
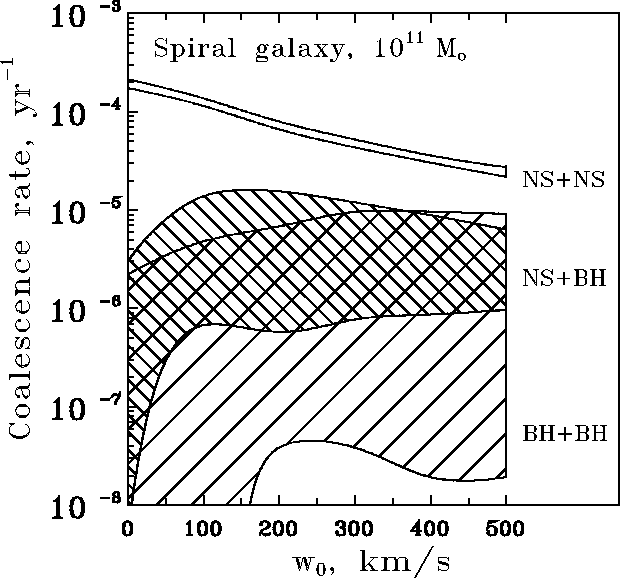
Figure: The dependence of different compact binary merging rates
in a spiral galaxy with ![]() M
M ![]() on the characteristic
kick velocity
on the characteristic
kick velocity ![]() .
.
After having found the merging rates R in a typical galaxy, we need to go over the event rate D at the detector. Applying the optimal filtering technique [21], the signal-to-noise ratio S/N at the spiral-in stage is
![]()
Here ![]() is ``chorp''-mass of the
binary system.
This means that for a given S/N our detector
can register more massive BH from larger distances
than NS. The volume within which BH or NS is to be detected
should be proportional
is ``chorp''-mass of the
binary system.
This means that for a given S/N our detector
can register more massive BH from larger distances
than NS. The volume within which BH or NS is to be detected
should be proportional ![]() . Then the ratio
of detection rates of BH and NS can be written as
. Then the ratio
of detection rates of BH and NS can be written as
![]()
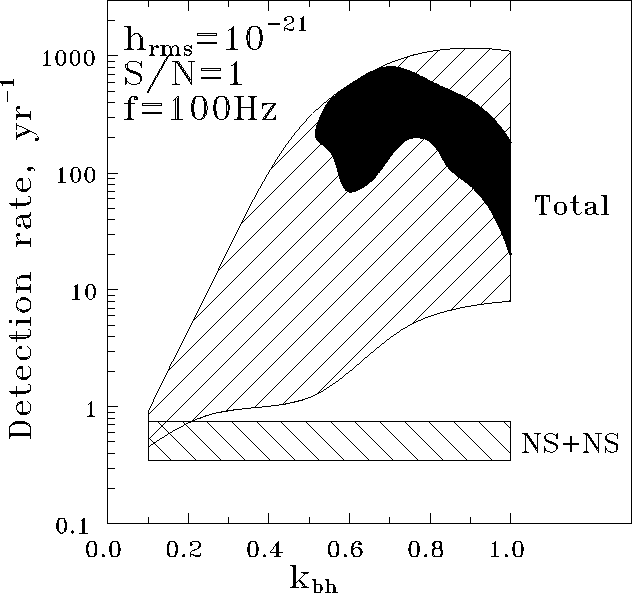
Figure: The total merging rate of NS+NS, NS+BH, and BH+BH binaries as
would be detected by a laser interferometer with ![]() for
Lyne-Lorimer kick velocity distribution with
for
Lyne-Lorimer kick velocity distribution with ![]() -400 km/s and BH
progenitor's masses
-400 km/s and BH
progenitor's masses ![]() -50M
-50M ![]() , for different scenarios of
binary star evolution as a function of
, for different scenarios of
binary star evolution as a function of ![]() . NS+NS mergings are
shown separately. In all cases BH+BH mergings contribute more than
. NS+NS mergings are
shown separately. In all cases BH+BH mergings contribute more than
![]() to the total rate. The filled ``Loch-Ness-monster-head''-like
region corresponds to BH formation parameters
to the total rate. The filled ``Loch-Ness-monster-head''-like
region corresponds to BH formation parameters
![]() M
M ![]() and
and ![]() .
.
Let us make a simple estimate. Take a GW detector
with ![]() and S/N=1 (as for the initial LIGO or
VIRGO interferometer). Let the mass of NS and BH be
1.4M
and S/N=1 (as for the initial LIGO or
VIRGO interferometer). Let the mass of NS and BH be
1.4M ![]() (the typical value well justified experimentally) and
8.5M
(the typical value well justified experimentally) and
8.5M ![]() (the mean mass of the BH candidates,
see Table
(the mean mass of the BH candidates,
see Table ![]() ). Let us also assume that any star with
the initial mass M(NS)>10M
). Let us also assume that any star with
the initial mass M(NS)>10M ![]() yields NS (the typical value
confirmed theoretically), and the threshold mass for BH formation
is the maximal from the estimates given above,
yields NS (the typical value
confirmed theoretically), and the threshold mass for BH formation
is the maximal from the estimates given above,
![]() M
M ![]() . Hence using Salpeter mass function
we find
. Hence using Salpeter mass function
we find
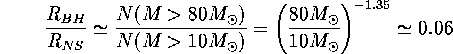
and then
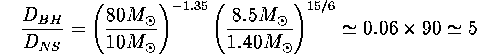
This estimate is, of course, very rough, but the precise calculation
gives essentially the same result. Fig. ![]() shows the
calculated absolute registration rate of mergings D by the detector
with
shows the
calculated absolute registration rate of mergings D by the detector
with ![]() and S/N=1, as a function of
and S/N=1, as a function of ![]() . The
calculations have been done for Lyne-Lorimer kick velocity distribution
with the parameter
. The
calculations have been done for Lyne-Lorimer kick velocity distribution
with the parameter ![]() ËÍ/Ó. The vertical dispersion is due to
the dependence of D on
ËÍ/Ó. The vertical dispersion is due to
the dependence of D on ![]() . It is seen that binary NS mergings
occur with a rate of about 1 event per year. In the same time, the
total detection rate (except for
. It is seen that binary NS mergings
occur with a rate of about 1 event per year. In the same time, the
total detection rate (except for ![]() ) can exceed that of
binary NS mergings by 2-3 orders. The filled region shows the region
of the ``most probable parameters'', for which the calculations meet both
the upper limit to the number of BH with radiopulsars (less than 1 per
700 single pulsars) and the number of BH candidates of Cyg X-1 type
(from 1 to 10 in the Galaxy). In this region, from 10 to 100 mergings
per year must be detected, with the majority of them being binary BH
mergings.
) can exceed that of
binary NS mergings by 2-3 orders. The filled region shows the region
of the ``most probable parameters'', for which the calculations meet both
the upper limit to the number of BH with radiopulsars (less than 1 per
700 single pulsars) and the number of BH candidates of Cyg X-1 type
(from 1 to 10 in the Galaxy). In this region, from 10 to 100 mergings
per year must be detected, with the majority of them being binary BH
mergings.