Next: Dependence on the Scenario Up: The Scenario Machine: Operational Previous: The Scenario Machine: Operational
![]()
![]()
![]()
![]()
![]()
Next: Dependence
on the Scenario Up: The
Scenario Machine: Operational Previous: The
Scenario Machine: Operational
The evolution of a binary system can be described as the movement of
a point in the parameter space ![]() , constituting both physical quantities (such as masses of binary components,
their radii, luminosities, orbital period, etc., independently of direct
observational measurability of these values), and related ``logical'' statements
(such as whether the system is binary or not, whether the NS is a radio-
or X-ray pulsar or not, whether the radiation from the NS is observable
or fully absorbed by a stellar wind, and so on). Each binary traces a path
(which we will call a ``track'') in this space, in a way strictly determined
by the evolutionary scenario. Each such track emerges with a certain probability,
which can be expressed through the initial distribution functions of binary
systems, in other terms, through the probability for a binary to be formed
with given initial parameters and age. Thus, one can introduce a probability
density p in the parameter space
, constituting both physical quantities (such as masses of binary components,
their radii, luminosities, orbital period, etc., independently of direct
observational measurability of these values), and related ``logical'' statements
(such as whether the system is binary or not, whether the NS is a radio-
or X-ray pulsar or not, whether the radiation from the NS is observable
or fully absorbed by a stellar wind, and so on). Each binary traces a path
(which we will call a ``track'') in this space, in a way strictly determined
by the evolutionary scenario. Each such track emerges with a certain probability,
which can be expressed through the initial distribution functions of binary
systems, in other terms, through the probability for a binary to be formed
with given initial parameters and age. Thus, one can introduce a probability
density p in the parameter space ![]() .
.
The most typical questions to be answered with the help of our Scenario Machine are, among others:
Clearly, the first two questions lead to the computation of some integrals
over the volume ![]() . One possible method which is convenient enough for this task is the Monte-Carlo
method. To determine what fraction of binaries of a
modeled galaxy will be found in volume
. One possible method which is convenient enough for this task is the Monte-Carlo
method. To determine what fraction of binaries of a
modeled galaxy will be found in volume ![]() of the parameter space, we must calculate the ratio of the time
of the parameter space, we must calculate the ratio of the time ![]() the binary remains inside
the binary remains inside ![]() , averaged over all tracks, to the mean duration of all tracks
, averaged over all tracks, to the mean duration of all tracks ![]()
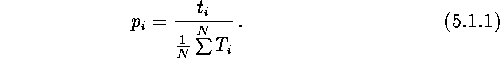
For this task to be fulfilled accurately, a large enough number N of evolutionary tracks within a wide range of the initial parameters distributed in accordance with given functions of probability distribution needs to be calculated, and the following quantities must be specified:
Then the fraction of binaries lying inside ![]() is expressed by
is expressed by
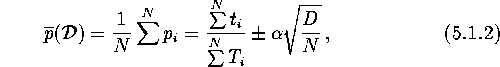
where ![]() is a coefficient defined by a confidence level, and the dispersion D
is defined as
is a coefficient defined by a confidence level, and the dispersion D
is defined as
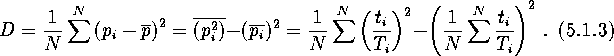
To obtain the absolute number of specified binary types, one needs to
multiply the quantity ![]() by the ratio of the total number of stars in the modeled galaxy
by the ratio of the total number of stars in the modeled galaxy ![]() to the actual number of modeled tracks N:
to the actual number of modeled tracks N:
![]()
To obtain the mean value of some parameter x
for the binaries from the volume ![]() of the parameter space
of the parameter space ![]() for N modeled tracks, one needs to calculate
quantities
for N modeled tracks, one needs to calculate
quantities ![]() and
and ![]() . Then the mean value
. Then the mean value ![]() is:
is:
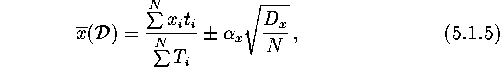
where ![]() is a confidence level, and the variance
is a confidence level, and the variance ![]() is
is
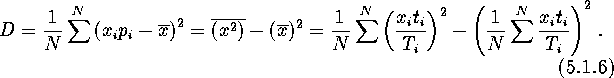
Note that all expressions written above can be obtained within the framework of a standard Monte-Carlo method (see, e.g., Sobol' 1973[183]).