Wolf-Rayet and He stars Principal Evolutionary States of Post main sequence stars

Roche lobe overflow (stage III)

 

The star fills its RL and begins to transfer matter on to the companion. The mass transfer first proceeds on the thermal time-scale (see detailed discussion in van den Heuvel, 1994[205])

The common envelope stage (CE)  may be formed if the RL overflow occurs in the type C systems (in which the primary component has a well developed (degenerate) core) even for q<1; otherwise (for the type B systems), we use the condition for the CE stage to occur. The radius of the star at the RL filling stage is taken to be that of the equivalent RL (Eggleton 1983[46]):

Here a is the binary separation and e is the orbital eccentricity.

We distinguish different substages of RL overflow according to characteristic time-scales of the mass transfer:

Stage III. RL overflow on a thermal time-scale.  This is the most frequent case for the first mass transfer phase.

Stage IIIe. Slow (evolutionary driven) phase of mass transfer. We assume it to occur for short-period A-type binaries. However, it may occur after mass reversal during the first stage of mass exchange for B-type binaries (van den Heuvel, 1994[205]), e.g. in wide low-mass X-ray binaries.

Stage IIIs. This stage is specific to superaccreting compact companions, a shortened substage of fast mass transfer when the matter escapes from the secondary companion carrying away its orbital angular momentum. Its duration is equal to

here and below subscripts ``a'' and ``d'' refer to the accreting and donating mass star, respectively. For systems with small mass ratios, q<0.5, this time-scale corresponds to an effective q-time shortening of the thermal time for the RL overflowing star.

Stages IIIm,g. Mass transfer is controlled by additional losses of orbital angular momentum caused by magnetic stellar wind (MSW)  or gravitational radiation (GW).  Characteristic time of evolution is defined as , and in the case of MSW is (Verbunt and Zwaan, 1981[209]; Iben and Tutukov, 1987[75])

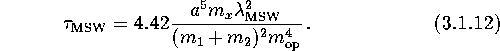
Here means the mass of the low-mass optical star (0.3<m<1.5), which is capable of producing an effective MSW, is a numerical parameter of order of unity. We used the mass-radius relation for main sequence stars in deriving this formula.

Gravitational radiation time is

The evolution is governed by MSW or GW if or is the shortest time-scale among all appropriate evolutionary time-scales.

Stage IIIwd. A special case when a WD overfills its RL. This stage is encountered for very short-period binaries (like 4U 1820-30) whose orbital evolution is controlled by GW or MSW losses. In order to calculate the mass loss  rate at each of the III-stages, in the vast majority of cases we use the prescription

where is the a priori known mass to be lost during the mass exchange phase (e.g., in the case of the conservative stage III, or in the case of III(e,m,g) or CE) and is the appropriate time-scale.

If one component overflows its RL, we assume the semi-major axis to change in such a way so that the donating mass star (either a normal low-mass star or a degenerate dwarf) keeps filling its RL,

Wolf-Rayet and He stars Principal Evolutionary States of Post main sequence stars