В данном приложении вычислим параметр ![]() .
Рассмотрим электромагнитное излучение с точки зрения квантовой
теории как поток элементарных частиц, называемых фотонами.
Следовательно, спектральную плотность потока фотонов можно
определить следующим соотношением:
.
Рассмотрим электромагнитное излучение с точки зрения квантовой
теории как поток элементарных частиц, называемых фотонами.
Следовательно, спектральную плотность потока фотонов можно
определить следующим соотношением:
Учитывая, что излучение Солнца является изотропным по всем
направлениям, то количество энергии, прошедшее через поверхность
Солнца ![]() , будет равно количеству энергии, прошедшему
через сферу радиуса
, будет равно количеству энергии, прошедшему
через сферу радиуса ![]() (
(![]() - расстояние от центра Солнца
до частицы, смотри рис. 21) 10. T.е.
- расстояние от центра Солнца
до частицы, смотри рис. 21) 10. T.е.
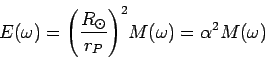 |
(54) |
Как показывают исследования, Солнце ведет себя в актах испускания
и поглощения излучения подобно абсолютно черному телу.
Следовательно, для ![]() мы можем использовать формулу
Планка для испускательной способности АЧТ:
мы можем использовать формулу
Планка для испускательной способности АЧТ:
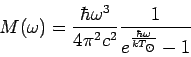 |
(55) |
| |
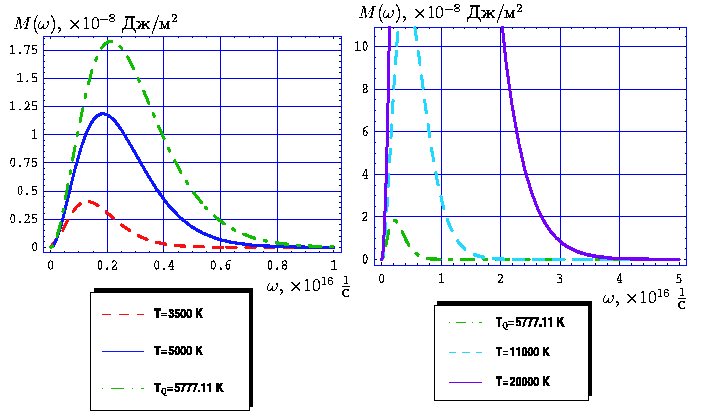
| Рис. 22. Зависимость спектральной испускательной способности абсолютно черного тела (звезды) от частоты излучения при различных температурах: T=3500 K (Антарес, α Скорпиона), T=5000 K (Арктур, α Волопаса), T=5777.11 K (Солнце). | Рис. 23. Зависимость спектральной испускательной способности абсолютно черного тела (звезды) от частоты излучения при различных температурах: T=5777.11 K (Солнце), T=11 000 K (Вега, α Лиры), T=20 000 K (Спика А, α Девы). |
Следовательно,
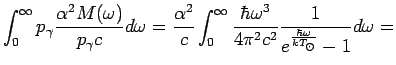 |
|||
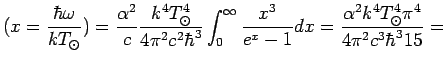 |
|||
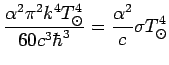 |
(56) |