Как было уже показано выше, для вычисления силы
светового давления необходимо знать явную функциональную
зависимость коэффициента отражения ![]() от угла падения
от угла падения
![]() (смотри выражения (16)-(18)).
Поэтому данное приложение посвящено поиску упомянутой зависимости
на основе волновых представлений об электромагнитном излучении,
распространяющемся в диэлектрических средах.
(смотри выражения (16)-(18)).
Поэтому данное приложение посвящено поиску упомянутой зависимости
на основе волновых представлений об электромагнитном излучении,
распространяющемся в диэлектрических средах.
Для нахождения этой зависимости рассмотрим процесс отражения
плоской электромагнитной волны на границе двух
диэлектриков с диэлектрическими проницаемостями ![]() ,
,
![]() , и с абсолютными показателями преломления
, и с абсолютными показателями преломления
![]() и
и ![]() , соответственно.
Как известно, любую плоскую
электромагнитную волну можно представить в виде суперпозиции двух
плоских волн, в одной из которых колебания совершаются в плоскости
падения, а в другой перпендикулярно к этой плоскости. Амплитуду
первой волны для падающей волны мы обозначим через
, соответственно.
Как известно, любую плоскую
электромагнитную волну можно представить в виде суперпозиции двух
плоских волн, в одной из которых колебания совершаются в плоскости
падения, а в другой перпендикулярно к этой плоскости. Амплитуду
первой волны для падающей волны мы обозначим через
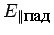 , а для второй -
, а для второй -
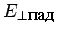 ,
в случае отраженной волны:
,
в случае отраженной волны:
 и
и
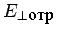 , соответственно. Между данными
амплитудами может быть установлена аналитическая связь,
представленная соотношениями Френеля [15].
, соответственно. Между данными
амплитудами может быть установлена аналитическая связь,
представленная соотношениями Френеля [15].
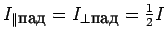 , где
, где
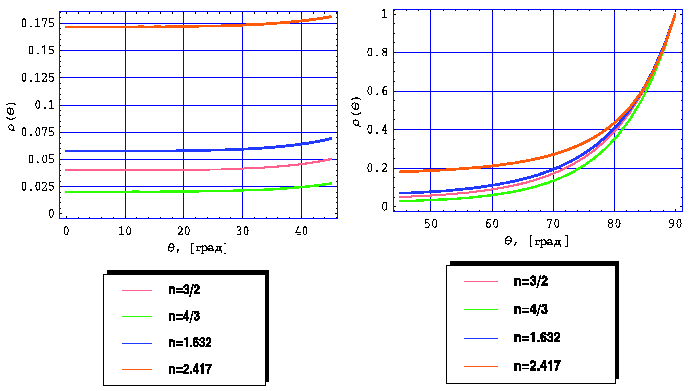
| |
| Рис. 24. Поведение коэффициента отражения ρ(θ) для указанных веществ в области малых углов падения (θ ε [0,45o]). | Рис. 25. Поведение коэффициента отражения ρ(θ) для указанных веществ в области больших углов падения (θ ε [45o,90o]). |
Рассмотрим функцию вида:
|
Таким образом, получено аналитическое выражение для коэффициента
отражения ![]() , при условии, что вещество, из которого
сделана частица, является диэлектриком с показателем преломления
, при условии, что вещество, из которого
сделана частица, является диэлектриком с показателем преломления
![]() и диэлектрической проницаемостью
и диэлектрической проницаемостью ![]() . Полученный
результат имеет большую ценность для решения поставленных задач в
данной работе, поскольку согласно классической модели ядро кометы
есть твердое тело, состоящее из легкоплавких веществ (льдов и
снегов), сублимирующихся под действием солнечного тепла
[2]. Исходя из наблюдаемого спектрального состава
кометных атмосфер, обычно считают, что льды состоят из твердых
. Полученный
результат имеет большую ценность для решения поставленных задач в
данной работе, поскольку согласно классической модели ядро кометы
есть твердое тело, состоящее из легкоплавких веществ (льдов и
снегов), сублимирующихся под действием солнечного тепла
[2]. Исходя из наблюдаемого спектрального состава
кометных атмосфер, обычно считают, что льды состоят из твердых
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и т.д. Данные
льды есть диэлектрические прозрачные среды, для которых применимы
все рассуждения, использованные для получения выражения
и т.д. Данные
льды есть диэлектрические прозрачные среды, для которых применимы
все рассуждения, использованные для получения выражения
![]() . В заключение, чтобы продемонстрировать поведение
результата (67), приведем графики зависимости
. В заключение, чтобы продемонстрировать поведение
результата (67), приведем графики зависимости
![]() для воды (
для воды (![]() ), стекла
(
), стекла
(![]() ), сероуглерода (
), сероуглерода (![]() ), алмаза (
), алмаза (![]() )
(смотри рис. 24-25). А
также в таблице 2, сопоставим экспериментальные
результаты для
)
(смотри рис. 24-25). А
также в таблице 2, сопоставим экспериментальные
результаты для ![]() [16], c результатами,
которые дает выражение (67) с учетом выражений
(64), (66), для воды
(
[16], c результатами,
которые дает выражение (67) с учетом выражений
(64), (66), для воды
(![]() ), и стекла (
), и стекла (![]() ). Из сопоставления данных
таблицы, очевидно, что аналитическое выражение
(67) хорошо описывает экспериментальные данные
(расхождение между теорией и экспериментом не превосходит
). Из сопоставления данных
таблицы, очевидно, что аналитическое выражение
(67) хорошо описывает экспериментальные данные
(расхождение между теорией и экспериментом не превосходит ![]() ).
).