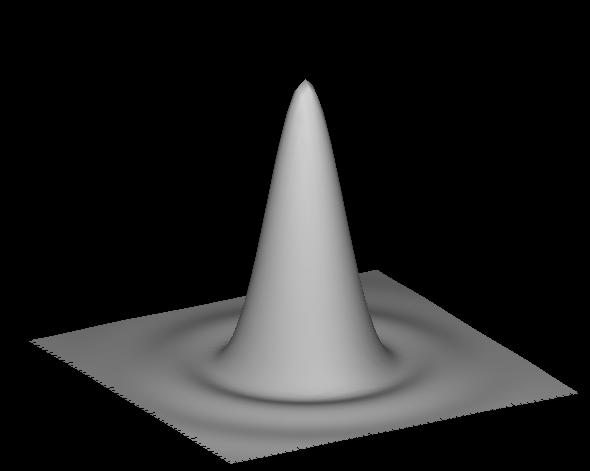
 Форма изображения точечного источника (звезды) в идеальном телескопе
без атмосферы определяется только дифракцией и описывается
функцией Эйри:
Форма изображения точечного источника (звезды) в идеальном телескопе
без атмосферы определяется только дифракцией и описывается
функцией Эйри:
Вверх: Введение
Далее: Деформируемые зеркала
 Форма изображения точечного источника (звезды) в идеальном телескопе
без атмосферы определяется только дифракцией и описывается
функцией Эйри:
Форма изображения точечного источника (звезды) в идеальном телескопе
без атмосферы определяется только дифракцией и описывается
функцией Эйри:
![\begin{displaymath}
P_0(\vec{\alpha}) = \frac{\pi D^2}{4 \lambda^2}
\left[ \fra...
.../\lambda)}{ \pi D \vert\vec{\alpha}\vert/\lambda)} \right] ^2,
\end{displaymath}](img1.gif) |
(1) |
Первое темное кольцо находится на угловом расстоянии
![]() от
центра. Часто это расстояние считается мерой разрешения идеального
телескопа.
от
центра. Часто это расстояние считается мерой разрешения идеального
телескопа.
Изображение
![]() астрономического объекта
астрономического объекта
![]() можно рассматривать как множество изображений точек, каждое
из которых описывается функцией Эйри. Это можно записать как
свертку:
можно рассматривать как множество изображений точек, каждое
из которых описывается функцией Эйри. Это можно записать как
свертку:
| (2) |
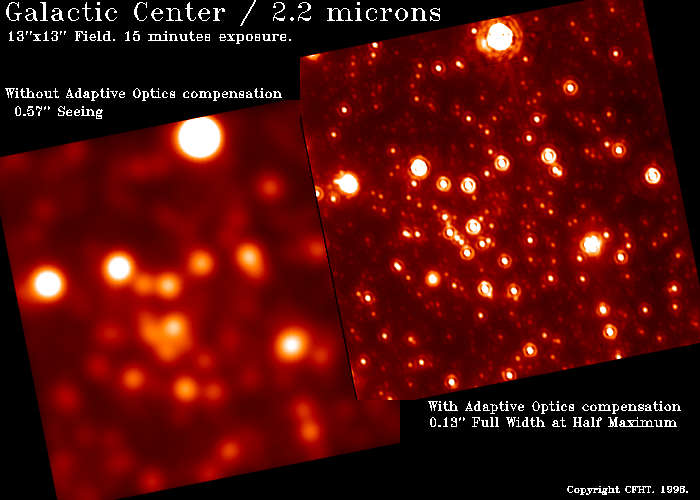
Вопрос: Как органиченное дифракцией разрешение зависит от длины волны?
Вопрос: Вычислите ограниченное дифракцией разрешение человеческого глаза.
Что произойдет, если телескоп не идеален? Изображение точечного
источника не будет так хорошо, как функция Эйри, разрешение ухудшится
еще сильнее.
Но уравнение изображения все равно останется в силе! Таким образом,
функция рассеяния точки (PSF)
![]() - это все, что нужно для характеристики изображения. Ширина PSF -
это мера разрешения.
- это все, что нужно для характеристики изображения. Ширина PSF -
это мера разрешения.
Замечание 1.
Мы неявно продполагаем, что в приведенных выше уравнениях
![]() описывает изображение звезды единичной интенсивности, т.е.
интеграл
описывает изображение звезды единичной интенсивности, т.е.
интеграл
![]() по
по ![]() равен 1. Таким образом, уравнение изображения сохраняет полный
поток от астрономического объекта, только по-разному распределяет
его по пикселам.
равен 1. Таким образом, уравнение изображения сохраняет полный
поток от астрономического объекта, только по-разному распределяет
его по пикселам.
Замечание 2. Мы предположили, что PSF имеет одинаковый вид по всему полю зрения. Это условие называется изопланатизмом. Для астрономических изображений это не всегда справедливо, особенно при использовании AO, так как PSF медленно изменяется по полю. В этом случае уравнение изображения можно применять к частям поля зрения.
Форма PSF может быть неправильной; как в этом случае количественно измерить разрешение?
1. Полная ширина на уровне половины максимума (FWHM) PSF.
2. Число Штреля
![]() ,
то есть центральная интенсивность PSF по сравнению с центральной
интенсивностью функции Эйри. Чем выше число Штреля, тем лучше разрешение.
Ограниченное дифракцией изображение - самое лучшее, так как всегда
,
то есть центральная интенсивность PSF по сравнению с центральной
интенсивностью функции Эйри. Чем выше число Штреля, тем лучше разрешение.
Ограниченное дифракцией изображение - самое лучшее, так как всегда
![]() .
.
3. Энергия в круге.
По определению, интеграл PSF равен 1. Интеграл от PSF в круге радиусом
![]() называется энергией в круге. Эта характеристика важна при
наблюдениях слабых объектов, когда необходимо как можно лучше
сконцентрировать фотоны.
называется энергией в круге. Эта характеристика важна при
наблюдениях слабых объектов, когда необходимо как можно лучше
сконцентрировать фотоны.
Пример PSF с исправлением турбулентности показан на рисунке ниже.
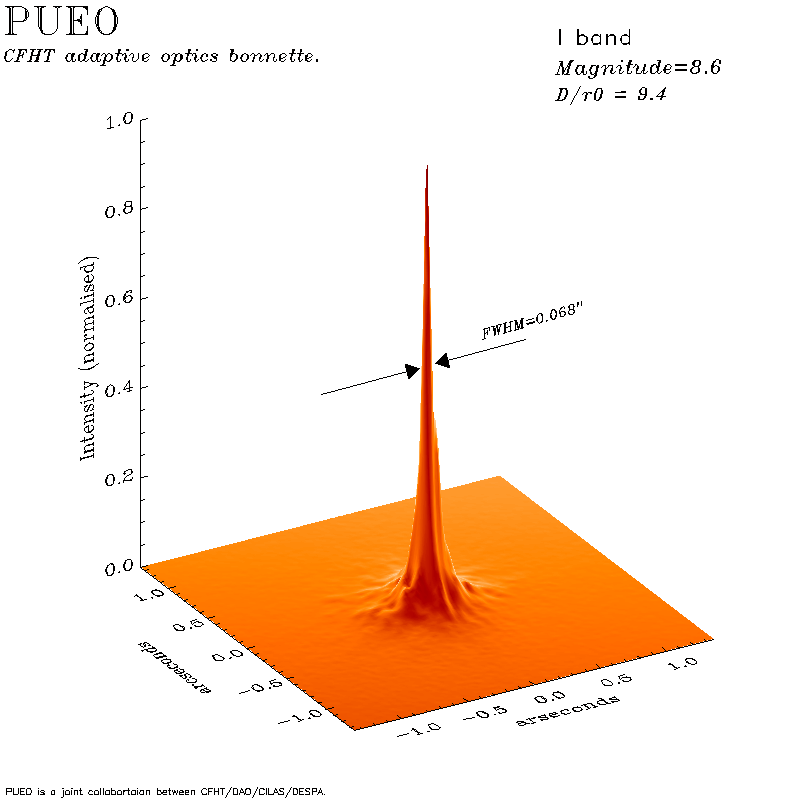
Вопрос: Предположим, что PSF стала в два раза уже, как изменится число Штреля?
Вопрос:
Каким будет число Штреля, если половине объектива идеального
телескопа дать фазовую задержку в
![]() ?
?
Другой способ описания уравнения изображения - это использование преобразований Фурье (FT, будем обозначать их тильдой). Свертка становится произведением, и
| (3) |
![]() называется оптической передаточной
функцией
(OTF).
Она описывает изменение модуля и фазы FT объекта в процессе получения
изображений. Модуль OTF называется
модуляционной передаточной функцией (MTF).
Для астрономических (некогерентных) изображений,
называется оптической передаточной
функцией
(OTF).
Она описывает изменение модуля и фазы FT объекта в процессе получения
изображений. Модуль OTF называется
модуляционной передаточной функцией (MTF).
Для астрономических (некогерентных) изображений,
![]() .
Обычно MTF уменьшается с увеличением частоты, поэтому мелкие
(высокочастотные) детали в изображении ослабляются и в конечном счете
теряются.
.
Обычно MTF уменьшается с увеличением частоты, поэтому мелкие
(высокочастотные) детали в изображении ослабляются и в конечном счете
теряются.
Известно, что для любой оптической системы
![]() для
для
![]() , где
, где
![]() называется частотой отсечки
,
называется частотой отсечки
, ![]() - максимальный размер апертуры. Это означает,
что информация о пространственных частотах выше
- максимальный размер апертуры. Это означает,
что информация о пространственных частотах выше
![]() безвозвратно теряется.
Чтобы увидеть маленькие объекты, нужны большие телескопы!
безвозвратно теряется.
Чтобы увидеть маленькие объекты, нужны большие телескопы!
Соотношение между PSF и OTF - это преобразование Фурье, поэтому
если вы знаете одну функцию, вы знаете и другую, это различные
представления одного явления. Из свойств преобразования Фурье следует,
что
![]() (нормировка PSF), и что число Штреля пропорционально интегралу
OTF по частотам.
(нормировка PSF), и что число Штреля пропорционально интегралу
OTF по частотам.
Вопрос: Какой минимальный размер телескопа потребуется, чтобы разрешить забор с промежутками между планками 10 см с расстояния в 5 км?
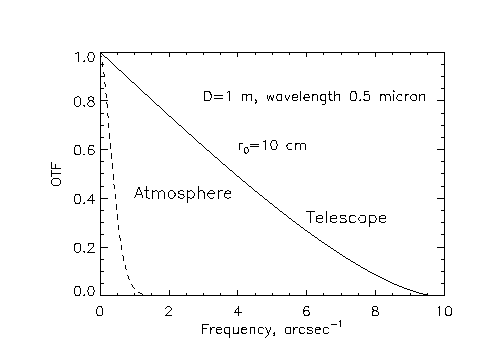 Атмосферную турбулентность можно рассматривать как случайную фазовую
аберрацию, приложенную к телескопу. Эти аберрации постоянно изменяются
со временем, и так же ведет себя PSF. Здесь мы рассмотрим среднюю
PSF, соответствующую длинным экспозициям. Из теории следует выражение
Атмосферную турбулентность можно рассматривать как случайную фазовую
аберрацию, приложенную к телескопу. Эти аберрации постоянно изменяются
со временем, и так же ведет себя PSF. Здесь мы рассмотрим среднюю
PSF, соответствующую длинным экспозициям. Из теории следует выражение
| (4) |
OTF атмосферы связана со статистикой атмосферных фазовых аберраций,
так называемой
фазовой структурной функцией
![]() (смотри следующий раздел):
(смотри следующий раздел):
| (5) |
Вопрос: Предположим, что форма атмосферной PSF - гауссова. Какова соответствующая форма структурной функции?
Вопрос:
Зависит ли форма атмосферной PSF от структурной функции в области, где
![]() and
and
![]() ?
?
Искаженный атмосферой волновой фронт можно представить как смятый лист бумаги. Волна, приходящая от звезды, перед вхождением в атмосферу плоская. Затем некоторые ее части проходят через воздух теплее среднего (меньший показатель преломления) и уходят вперед, другие части отстают, и плоский волновой фронт деформируется. Задача адаптивной оптики - скомпенсировать эти искажения. Но вначале мы должны описать их в статистическом смысле.
Воздух обладает некоторой дисперсионной способностью, но обычно
этим пренебрегают, и возмущения оптического пути
![]() рассматриваются как ахроматичные.
Однако,
фаза оптической волны
рассматриваются как ахроматичные.
Однако,
фаза оптической волны
![]() сильно зависит от длины волны
сильно зависит от длины волны
![]() !
Говоря о возмущениях, мы предполагаем, что их среднее значение равно
нулю,
!
Говоря о возмущениях, мы предполагаем, что их среднее значение равно
нулю,
![]() (угловые скобки обозначают статистическое усреднение).
(угловые скобки обозначают статистическое усреднение).
Хотя случайные процессы, подобные
![]() обычно описываются корреляционными или ковариционными функциями,
в исследованиях атмосферы предпочитают
структурные функции.
Структурная функция - это средняя разность между двумя значениями
случайного процесса:
обычно описываются корреляционными или ковариционными функциями,
в исследованиях атмосферы предпочитают
структурные функции.
Структурная функция - это средняя разность между двумя значениями
случайного процесса:
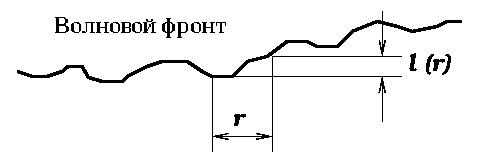
| (6) |
Вопрос:
Каково соотношение между структурной функцией и функцией ковариации
![]() ?
?
Вопрос:
Как атмосферная
![]() зависит от
длины волны
зависит от
длины волны ![]() ?
?
 Колмогоровская модель
турбулентных искажений задает определенную форму фазовой структурной
функции, а именно
Колмогоровская модель
турбулентных искажений задает определенную форму фазовой структурной
функции, а именно
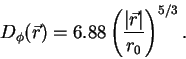 |
(7) |
Эта модель, хотя она и может показаться примитивной, является основанием всей теории получения изображений сквозь турбулентность, включая адаптивную оптику. Конечно, модель плохо работает на больших (больше нескольких метров) и малых (меньше 1 см) расстояниях, но оказывается, что это не очень важно.
Ворпос:
Каково среднеквадратичное различие атмосферной фазы на длине базы
![]() в радианах и в длинах волн?
в радианах и в длинах волн?
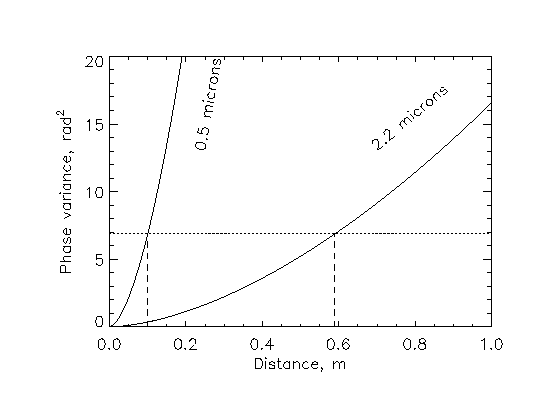
Вопрос: Если ![]() см на длине волны 0.5 микрон, то чему равно
см на длине волны 0.5 микрон, то чему равно
![]() на длине волны 2.2 микрона?
на длине волны 2.2 микрона?
Теперь мы подставим эту модель в атмосферную OTF для длинных экспозиций, и получим ее в форме:
| (8) |
| (9) |
Число Штреля атмосферной PSF точно такое же, как для идеального
телескопа диаметром
![]() (это причина появления странного коэффициента 6.88)
Таким образом, для большого телескопа
(это причина появления странного коэффициента 6.88)
Таким образом, для большого телескопа
![]() ,
число Штреля равно просто
,
число Штреля равно просто ![]() .
.
Вопрос: Чему равно число Штреля для изображения с длинной экспозицией для 4-м телескопа при качестве изображения 1 секунда на длинах волн 0.5 и 2.2 микрона?
Радиус Фрида ![]() иногда отождествляют с характерной шкалой атмосферных возмущений.
Это не совсем верно: мы видим, что закон Колмогорова не имеет
какой-либо характерной шкалы. Однако, только возмущения с размером
порядка
иногда отождествляют с характерной шкалой атмосферных возмущений.
Это не совсем верно: мы видим, что закон Колмогорова не имеет
какой-либо характерной шкалы. Однако, только возмущения с размером
порядка
![]() имеют значение для изображений с длинными экспозициями.
На меньших размерах искажения много меньше, чем
имеют значение для изображений с длинными экспозициями.
На меньших размерах искажения много меньше, чем
![]() , на больших размерах
, на больших размерах ![]() становится таким большим, что
атмосферная OTF равна нулю.
становится таким большим, что
атмосферная OTF равна нулю.
Локальная величина турбулентных флуктуаций индекса преломления в
воздухе описывается структурной постоянной индекса преломления
![]() который измеряется в странных единицах,
m
который измеряется в странных единицах,
m![]() .
Зависимость
.
Зависимость
![]() от высоты называется профилем турбулентности. Качество изображения
зависит от суммарного влияния всех слоев атмосферы:
от высоты называется профилем турбулентности. Качество изображения
зависит от суммарного влияния всех слоев атмосферы:
| (10) |
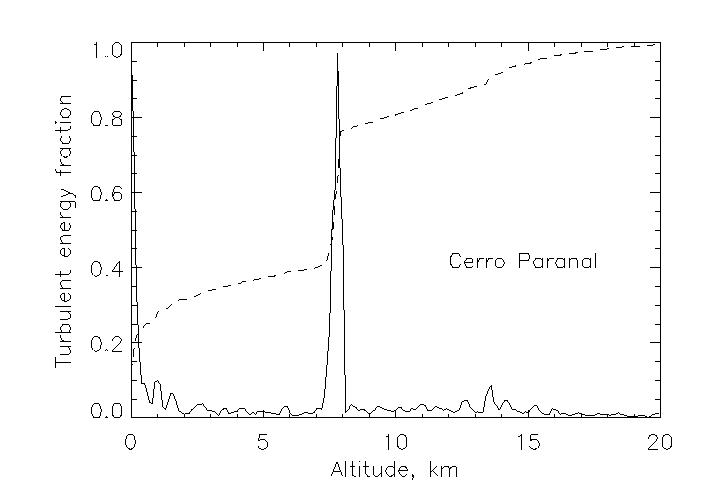 .
.
На этом рисунке показан пример профиля турбулентности в относительных единицах в Серро Паранал (сплошная линия). Доля турбулентной энергии до данной высоты показана штриховой линией. Хотя в этом примере значительная часть турбулентности сконцентрирована в двух слоях, все же около 1/3 общей энергии равномерно распределено по всем высотам.
Вопрос: Используя это соотношение,
найдите, как
![]() и качество изображения зависят от зенитного угла
и качество изображения зависят от зенитного угла
![]() .
.
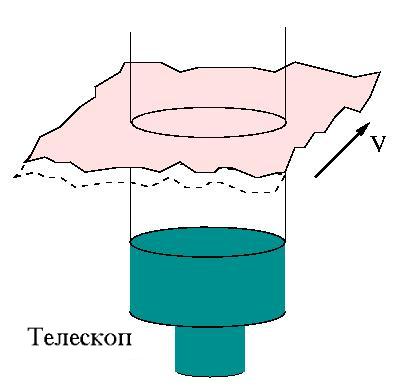 Часто турбулентность можно смоделировать как экраны,
дающие постоянный сдвиг фазы,
которые перемещаются ветром перед телескопом. Зная пространственные
свойства фазовых экранов (структурную функцию) и скорость ветра,
можно установить временное поведение возмущений.
Атмосферная постоянная времени
Часто турбулентность можно смоделировать как экраны,
дающие постоянный сдвиг фазы,
которые перемещаются ветром перед телескопом. Зная пространственные
свойства фазовых экранов (структурную функцию) и скорость ветра,
можно установить временное поведение возмущений.
Атмосферная постоянная времени
![]() определяется как
определяется как
| (11) |
Вопрос:
Взяв типичное значение
![]() =20 м/с,
какой будет атмосферная постоянная времени на длинах волн 0.5 и
2.2 микрона при качестве изображения 1 секунда?
=20 м/с,
какой будет атмосферная постоянная времени на длинах волн 0.5 и
2.2 микрона при качестве изображения 1 секунда?
Изображения астрономических объектов, полученные с экспозициями
![]() или короче, называются изображениями с короткими экспозициями.
Они соответствуют фиксированным (замороженным) атмосферным аберрациям.
Для более длинных экспозиций аберрации усредняются, и для экспозиций,
намного длиннее
или короче, называются изображениями с короткими экспозициями.
Они соответствуют фиксированным (замороженным) атмосферным аберрациям.
Для более длинных экспозиций аберрации усредняются, и для экспозиций,
намного длиннее
![]() можно получить PSF для длинных экспозиций.
можно получить PSF для длинных экспозиций.
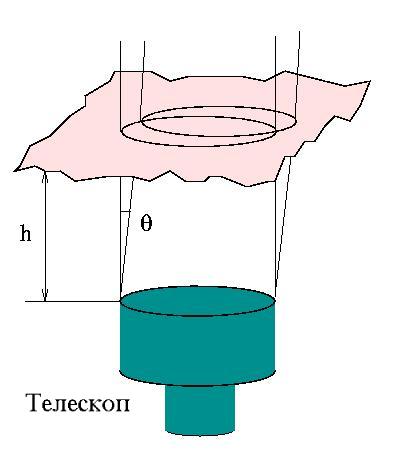 Атмосферная PSF для длинных экспозиций не зависит от направления
(изопланатична), так как турбулентность и ее структурная функция
статистически одинаковы в поле зрения. Однако моментальные
атмосферные фазовые аберрации зависят от направления: для
углового расстояния 10 секунд смещение луча зрения телескопа
в атмосферном слое на высоте 10 км составит 0.5 м.
Атмосферная PSF для длинных экспозиций не зависит от направления
(изопланатична), так как турбулентность и ее структурная функция
статистически одинаковы в поле зрения. Однако моментальные
атмосферные фазовые аберрации зависят от направления: для
углового расстояния 10 секунд смещение луча зрения телескопа
в атмосферном слое на высоте 10 км составит 0.5 м.
Стандартное определение атмосферного изопланатического угла
![]() - это
- это
|
|
(12) |
Вопрос: Чему равен
изопланатический угол ![]() для
длин волн 0.5 и 2.2 микрона при качестве изображения 1 секунда?
для
длин волн 0.5 и 2.2 микрона при качестве изображения 1 секунда?
Это явление представляет очень большую проблему для адаптивной оптики, так как оно ограничивает расстояние между опорной звездой и исследуемым объектом. Оказывается, что для большинства объектов нет подходящих (ярких и близких) опорных звезд, поэтому необходимы искусственные лазерные опорные звезды. Как альтернативный метод, для увеличения исправляемого поля зрения можно попытаться применить трехмерное исправление турбулентности ( мульти-сопряженную адаптивную оптику, MCAO).
В оптике аберрации часто представляют суммой специальных полиномов, называемых полиномами Зернике. Случайные атмосферные аберрации можно представить в том же виде; однако, коэффициенты этих аберраций (расфокусировки, астигматизма и т.д.) будут случайными функциями, изменяющимися со временем.
Полиномы Зернике
![]() определяются в полярных координатах
определяются в полярных координатах
![]() на окружности с единичным радиусом
на окружности с единичным радиусом
![]() .
Они характеризуются
радиальным порядком
.
Они характеризуются
радиальным порядком ![]() и азимутальным порядком
и азимутальным порядком
![]() (для данного
(для данного
![]() ,
, ![]() принимает значения от 0 до
принимает значения от 0 до ![]() ).
Часто вместо двух индексов
).
Часто вместо двух индексов
![]() и
и ![]() используется последовательная нумерация с одним индексом
используется последовательная нумерация с одним индексом
![]() .
Для данного радиального порядка
.
Для данного радиального порядка
![]() существует
существует
![]() полиномов Зернике.
полиномов Зернике.
Первые моды Зернике названы так же, как известные аберрации, и имеют простой смысл (смотри таблицу первых 15 мод Зернике).
Преимущества использования мод Зернике вытекают из того, что они
являются ортонормальными, то есть скалярное произведение
![]() равно 1, если
равно 1, если
![]() и равно нулю в других случаях. Скалярное произведение определяется
как интеграл по апертуре телескопа:
и равно нулю в других случаях. Скалярное произведение определяется
как интеграл по апертуре телескопа:
| (13) |
Теперь любая фазовая аберрация
![]() внутри зрачка телескопа может быть представлена как
бесконечная сумма полиномов Зернике
внутри зрачка телескопа может быть представлена как
бесконечная сумма полиномов Зернике
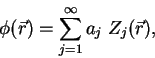 |
(14) |
| (15) |
Часто ограниченное число мод Зернике уже дает достаточно хорошее представление атмосферных аберраций. Если эти моды исправляются адаптивной оптикой, то получается изображение с качеством, практически неотличимым от определяемого дифракцией.
Мода поршень соответствует постоянной фазе, которая не влияет на изображение. Обычно эта мода игнорируется.
Вопрос: 4-м телескоп ![]() , расфокусирован на 1 мм.
Вычислите возникающую аберрацию
, расфокусирован на 1 мм.
Вычислите возникающую аберрацию ![]() для длин волн 0.5 и 2.2 микрона.
для длин волн 0.5 и 2.2 микрона.
Вопрос:
Предположим, что атмосферная аберрация содержит только случайные
наклоны с одинаковыми амплитудами
![]() .
Запишите соответствующую фазовую структурную функцию.
.
Запишите соответствующую фазовую структурную функцию.
Ортонормальность мод Зернике предоставляет простую возможность
вычислить дисперсию фазы, проинтегрированную по зрачку. Для одной
моды это
![]() .
Дисперсия всех мод равна сумме квадратов коэффициентов, начиная с второго
(поршень исключается).
.
Дисперсия всех мод равна сумме квадратов коэффициентов, начиная с второго
(поршень исключается).
В рамках модели турбулентности Колмогорова мы можем получить
статистические свойства коэффициентов
![]() ,
соответствующих атмосферным фазовым аберрациям.
Математические преобразования приводят к простой формуле:
,
соответствующих атмосферным фазовым аберрациям.
Математические преобразования приводят к простой формуле:
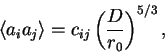 |
(16) |
| i \ j | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 0.449 | 0 | 0 | 0 | 0 | 0 | 0.0142 | 0 | 0 |
| 3 | 0 | 0.449 | 0 | 0 | 0 | 0.0142 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0.0232 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0.0232 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0.0232 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0.0142 | 0 | 0 | 0 | 0.00619 | 0 | 0 | 0 |
| 8 | 0.0142 | 0 | 0 | 0 | 0 | 0 | 0.00619 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.00619 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.00619 |
Как вы видите, матрица Нолля почти диагональная (однако для
более высоких порядков это уже не так). Почему коэффициент
![]() отсутствует? Для колмогоровской турбулентности он бесконечен!
Однако первая мода (поршень) не имеет значения для изображений.
отсутствует? Для колмогоровской турбулентности он бесконечен!
Однако первая мода (поршень) не имеет значения для изображений.
Вопрос: Для 4-м телескопа и качества изображения 1 секунда, вычислите среднеквадратичную амплитуду наклона в радианах (для длины волны 0.5 микрон). Переведите ее в среднеквадратичную амплитуду движения изображения звезды. Зависит ли эта амплитуда от длины волны?
Что произойдет, если мы исправим первые моды с помощью адаптивной
оптики? Соответствующие коэффициенты обратятся в нули, и полная
дисперсия фазы уменьшится. Обозначая усредненную по зрачку дисперсию фазы
как
![]() , мы запишем
, мы запишем
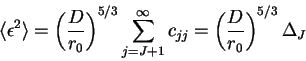 |
(17) |
Полная неисправленная атмосферная фазовая дисперсия (все моды кроме
поршня) соответствует
![]() .
Другими словами, в телескопе с диаметром апертуры
.
Другими словами, в телескопе с диаметром апертуры
![]() атмосферная фазовая дисперсия составляет примерно 1 квадратный радиан.
Если наклоны исправлены, то
атмосферная фазовая дисперсия составляет примерно 1 квадратный радиан.
Если наклоны исправлены, то
![]() .
Это означает, что наклоны составляют 87% полной дисперсии фазы.
Исправляя моды до радиального порядка 2, получим
.
Это означает, что наклоны составляют 87% полной дисперсии фазы.
Исправляя моды до радиального порядка 2, получим
![]() ,
радиальный порядок 3 оставляет неисправленную дисперсию
,
радиальный порядок 3 оставляет неисправленную дисперсию
![]() .
Как вы видите, дальнейшее уменьшение дисперсии фазы требует
исправления все большего числа мод Зернике.
.
Как вы видите, дальнейшее уменьшение дисперсии фазы требует
исправления все большего числа мод Зернике.
Для большого число исправленных мод
![]() (
(![]() ,
что происходит в реальных системах), очень полезна
асимптотическая формула Нолля:
,
что происходит в реальных системах), очень полезна
асимптотическая формула Нолля:
| (18) |
Вопрос: Используя значения ![]() и
и ![]() данные выше, вычислите
данные выше, вычислите
![]() .
.
Сколько мод нужно исправить? Оптики знают, что когда остаточная
фаза меньше 1 радиана, качество изображения приближается к
ограниченному дифракцией. Теперь у нас есть все, чтобы определить
необходимое число мод как функцию диаметра телескопа, качества
изображения и длины волны! Достаточно записать
![]() и подставить сюда все формулы ( попытайтесь сделать это!).
В результате получим
и подставить сюда все формулы ( попытайтесь сделать это!).
В результате получим
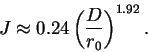 |
(19) |
Вопрос: Сколько мод Зернике необходимо исправить на 4-м телескопе для изображений на длинах волн 0.5 и 2.2 микрона при качестве изображения 1 секунда?
Необходимо ли исправлять турбулентность, используя моды Зернике? Разумеется, нет, фазовые аберрации могут быть измерены и исправлены с помощью любого другого набора базовых функций, или вообще без всяких мод, непосредственно воздействуя на волновой фронт. Оказывается, что моды Зернике - это второй по качеству набор мод (лучший набор называется модами Карунена-Лоева). Выбор зависит от числа контролируемых параметров (мод), необходимого для достижения требуемой степени исправления; для мод Зернике оно меньше, чем для локального контроля волнового фронта.
Выводы.
В этой главе были кратко изложены основы получения изображения в
идеальном телескопе и с присутствием аберраций (PSF, OTF, ограничение
дифракцией, число Штреля). Затем были введены основные параметры
атмосферы, имеющие отношение к адаптивной оптике (фазовая структурная
функция, качество изображения,
![]() ,
постоянная времени и изопланатический угол).
Исследовано разложение случайных фазовых аберраций по модам Зернике.
Теперь мы можем определить число мод, которые необходимо исправить.
,
постоянная времени и изопланатический угол).
Исследовано разложение случайных фазовых аберраций по модам Зернике.
Теперь мы можем определить число мод, которые необходимо исправить.
ВВЕРХ: Введение
ДАЛЕЕ: Деформируемые зеркала