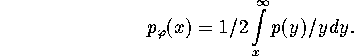The initial velocity of young neutron
stars can be taken either from the observed pulsar velocity distribution (which
is still not firmly established), or from some model-dependendent
assumptions based on current ideas about neutron star formation.
Both ways are not seemed to be problem free. Here we will use
the second way, that is we will calculate initial velocity
of a new-born pulsar as the sum of its regular velocity in the
Galaxy and a velocity which the pulsar
acquires at the moment of the burth. The former is defined by
the assumed galactic potential and is typically of order of 200 km/s, and
the latter is caused by a chaotic motion of the progenitor star and a
regular motion of the pulsar progenitor in a binary system and usually
km/s. We also
take into account possible assymetry in the supernova explosion mechanism
(for example, neutrino anisotropy
in a strong magnetic field (Chugaj 1984), breaking of magnetic
field symmetry during magneto-rotational collapse (Bisnovatyj-Kogan
& Moiseenko 1992) or splitting of fast rotating newborn neutron star into two
neutron stars with subsequent explosion of the easier component (Imshennik
and Nadyozhin 1992))
by introducing a ``kick'' velocity for the pulsar.
This ``kick'' velocity is supposed to be as high as
km/s and randomly oriented. (Note that if Imshennik and
Nadyozhin mechanism is actually under work, which is supposed to occur
in a few percent of supernovae, one should expect a subclass of very fast
moving pulsars ( 
km/s) to exist which ultimately
will populate a very extended halo around the Galaxy).
We have performed a Monte-Carlo calculation of evolution of
50,000 massive binaries with an initial mass of primary
star 
to obtain initial velocity
distribution of young pulsars. Description of
the method of statistical simulation we use can be found elsewhere
(Kornilov and Lipunov (1983) and Lipunov and Postnov (1987)). The
results are presenred in Fig.
. One can see that the velocity distribution
have a maximum centered on the value of the assumed
``kick'' velocity and high-velocity tail of the distribution
is obeyed a power law with a slope of 
.
This probably reflects a
power-law shape of the assumed (Salpeter) distribution for the
initial stellar masses, and power-law parametrization of binary
system evolutionary tracks we used for statistical calculations
of a large number of systems. We assume the distribution 
to be isotropical. At the same time we need know the distribution of
projected velocities on the direction of the systematic motion
in the Galaxy (i.e. on the direction of 
)
. This is
required because we need calculate distribution on energy E (which
depends on ) and on angular momentum 
(which is
determined by ). These two distribution are
connected through the well known relation
