Next: The Gravimagnetic Parameter Up: ``Ecology'' of Magnetic Rotators Previous: Nomenclature
![]()
![]()
![]()
![]()
![]()
Next: The
Gravimagnetic Parameter Up: ``Ecology''
of Magnetic Rotators Previous: Nomenclature
The classification given above was based on relations
between the characteristic radii, i.e. quantities which cannot be observed
directly. This drawback can be removed if we note that the light cylinder
radius ![]() , Schwartzman radius
, Schwartzman radius ![]() and corotation radius
and corotation radius ![]() are functions of the well-observed quantity, rotational period of the magnetor
p. Hence, the above classification can be reformulated in
the form of inequalities for the rotational period of a magnetic rotator.
are functions of the well-observed quantity, rotational period of the magnetor
p. Hence, the above classification can be reformulated in
the form of inequalities for the rotational period of a magnetic rotator.
One can introduce two critical periods ![]() and
and ![]() such that their relationship with period p
of a magnetic rotator specifies the rotator's type:
such that their relationship with period p
of a magnetic rotator specifies the rotator's type:
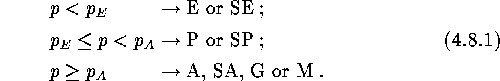
The values of ![]() and
and ![]() can be determined from Table 2
which defines the basic nomenclature, and are functions of the parameters
can be determined from Table 2
which defines the basic nomenclature, and are functions of the parameters
![]() ,
, ![]() ,
, ![]() and
and ![]() . The parameters p and
. The parameters p and ![]() characterize the electromagnetic interaction, while
characterize the electromagnetic interaction, while ![]() describes the gravitational interaction. Instead of
describes the gravitational interaction. Instead of ![]() , we introduce the potential accretion luminosity L
, we introduce the potential accretion luminosity L
![]()
The physical sense of the potential luminosity is quite clear: the accreting star would be observed to have this luminosity if the matter formally falling on the gravitational capture cross-section were to reach its surface.
Approximate expressions for critical periods (Lipunov 1992[107]) are
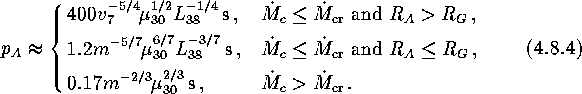
Here a new critical period ![]() was introduced from the condition
was introduced from the condition ![]() :
:
![]()
Treating the rotator's magnetic dipole moment ![]() and
and ![]() as parameters, we find that an overwhelming majority of the magnetor's
stages can be shown on a ``
as parameters, we find that an overwhelming majority of the magnetor's
stages can be shown on a `` ![]() '' diagram (Lipunov 1982a[98]). The quantity
L also proves to be convenient because
it can be observed directly at the accretion stage.
'' diagram (Lipunov 1982a[98]). The quantity
L also proves to be convenient because
it can be observed directly at the accretion stage.