Next: A Universal Diagram for Up: ``Ecology'' of Magnetic Rotators Previous: The Corotation Radius
Next: A
Universal Diagram for Up: ``Ecology''
of Magnetic Rotators Previous: The
Corotation Radius
The interaction of a magnetic rotator with the surrounding plasma to
a large extent depends on the relation between the four characteristic
radii: the stopping radius, 
, the gravitational capture radius, 
, the light cylinder radius, 
, and the corotation radius, 
. The difference between the interaction regimes is so significant that
the magnetic rotators behave entirely differently in
different regimes. Hence, the classification of the interaction regimes
may well mean the classification of magnetic rotators. The classification
notation and terminology is described below and summarized in Table 2,
based on paper by Lipunov (1987)[105].
Naturally, not all possible combinations of the characteristic radii
can be realized. For example, the inequality 
is not possible in principle. Furthermore, some combinations require unrealistically
large or small parameters of magnetic rotators. Under the same intrinsic
and external conditions, the same rotator may gradually pass through several
interaction regimes. Such a process will be referred to as the evolution
of a magnetic rotator.
We describe the classification by considering an idealized scenario
of evolution of magnetic rotators. Suppose the parameters 
, 
, and 
of the surrounding medium remain unchanged. We shall also assume for a
while a constancy of the rotator's magnetic moment 
. Let the potential accretion rate
at the beginning be not too high, so that the reverse effect of radiation
pressure can be neglected, 
. We also assume that the star initially rotates at a high enough speed
to provide a powerful relativistic wind.
Ejectors (E) We shall call a magnetic rotator
an ejecting star (or simply an ejector E, see Figure 5)
if the pressure of the electromagnetic radiation and ejected relativistic
particles is so high that the surrounding matter is swept away beyond the
capture radius or radius of the light cylinder (if 
):
It follows from here that 
, while the accretion pressure within the capture radius is 
, i.e. increases more rapidly as we approach an accreting star. Consequently,
the radius of a stable cavern must exceed the capture
radius (Schwartzman, 1970a[173]).
It is worth noting that the reverse transition from the propeller
(P) stage to the ejector (E) stage is non-symmetrical
and occurs at a lower period (see below). This means that to switch a pulsar
on is more difficult than to turn it off. This is due to the fact that
in the case of turning-on of the pulsar the pressures of plasma and relativistic
wind must be matched at the surface of the light cylinder,
not at the gravitational capture radius. In fact, the reverse transition
occurs under the condition of equality of the Alfvén radius to the radius
of the light cylinder ( 
, see Section 4.12.2 for more detail).
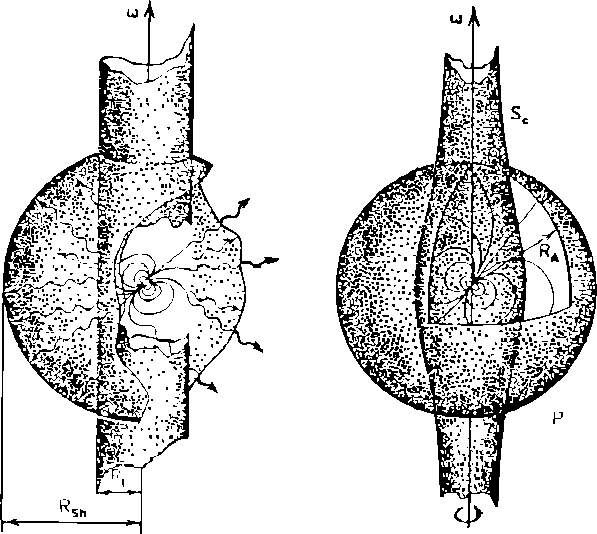
Figure 5: An ejector (left figure) and a propeller (right figure).
It should be emphasized that, as mentioned by Schwartzman (1970a)[173], relativistic particles can be formed also at the propeller stage by a rapidly rotating magnetic field (see also Kundt, 1990[92]).
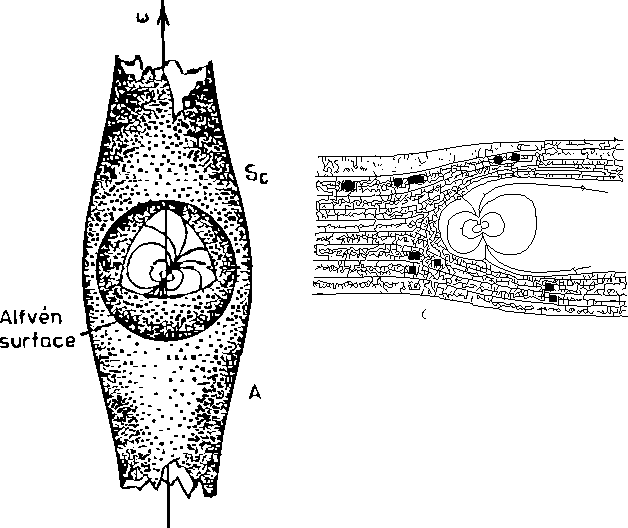
Figure 6: An accretor (left figure) and a georotator (right figure).
Propellers (P) After the ejector stage, the
propeller stage sets in under quite general conditions, when accreting
matter at the Alfvén surface is hampered by a rapidly rotating magnetic
field of the magnetic rotator (Figure 5).
In this regime the Alfvén radius is greater than the corotation radius,
. A finite magnetic viscosity causes the angular momentum to be transferred
to the accreting matter so that the rotator spins down.
Until now, the propeller stage is one of the poorly investigated phenomena.
However, it is clear that sooner or later the magnetic rotator is spin
down enough for the rotational effects to be of no importance any longer,
and the accretion stage sets in.
Accretors (A) In the accretion stage, the
stopping radius (Alfvén radius) must be smaller than the corotation radius
(Figure 6). This is the most thoroughly
investigated regime of interaction of magnetic rotators with accreting
plasma. Examples of such systems span a wide range of bright observational
phenomena from X-ray pulsars, X-ray bursters,
low-mass X-ray binaries to most of the cataclysmic variables
and X-ray transient sources.
Georotators (G) Imagine that the star begins rotating so slowly that it cannot impede the accretion of plasma, i.e. all the conditions mentioned in the previous paragraph are satisfied. However, matter still can not fall on to the rotator's surface if the Alfvén radius is larger than the gravitational capture radius (Illarionov and Sunyaev, 1975[76]; Lipunov, 1982e[102]). This means that the attractive gravitational force of the star at the Alfvén surface is not significant. A similar situation occurs in the interaction of solar wind with Earth's magnetosphere. The plasma mainly flows around the Earth's magnetosphere and recedes to infinity (Figure 6). This analogy explains the term ``georotator'' used for this stage. Clearly, a georotator must either have a strong magnetic field or be embedded in a strongly rarefied medium.
Magnetors (M) When a rotator enters a binary system, it may happen that its magnetosphere engulfs the secondary star. Such a regime was first considered by Mitrofanov et al. (1977)[142] for WD in close binary systems called polars due to their strongly polarized emission. In the case of NS, magnetors M may be realized only under the extreme condition of very close binaries with no matter within the binary separation (Figure 7). Supercritical interaction regimes So far, we have assumed that the luminosity at the stopping surface is lower than the Eddington limit. This is fully justified for G and M regimes since gravitation is not important for them. For types E, P, and especially A, however, this is not always true. The critical accretion rate for which the Eddington limit is achieved is
where 
cm is the stopping radius (Schwartzman radius or Alfvén
radius, see above) in units of 
cm.
We stress here that the widely used condition of supercritical accretion
rate 
yr 
is valid only for the case of non-magnetic NS, where 
km coincides with the stellar radius. In reality, for a NS with a typical
magnetic field of 
- 
G, the Alfvén radius reaches 
-
cm, so much higher accretion rates are required for the supercritical
accretion to set in. The electromagnetic luminosity released at the NS
surface, however, will be restricted by 
, and most of the liberated energy may be carried away by neutrinos
(Basko and Sunyaev, 1975[9]).
Most of the matter in the dynamic model of supercritical accretion forms an outflowing flux covering the magnetic rotator by an opaque shell (Shakura and Sunyaev, 1973). The following three additional types are distinguished, depending on the relationship between the characteristic radii (see Table 2): superejector (SE), superpropeller (SP) and superaccretor (SA) (see also Figure 8).
