Evolutionary Tracks Evolution of Magnetic Rotators The evolution equation

The equilibrium period

 

The evolution equation presented above indicates that an accreting compact star must endeavor to attain an equilibrium state in which the resultant torque vanishes (Davidson and Ostriker, 1973[38]; Lipunov and Shakura, 1976[109]). This hypothesis is confirmed by observations of X-ray pulsars. 

By equating the right-hand side of equation (4.10.2) to zero, we obtain the equilibrium period: 

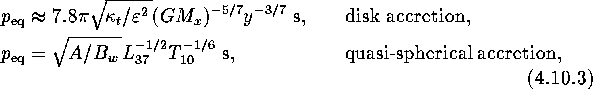
  where  s yr , and
 s yr , ,  days.

Alternatively:

 

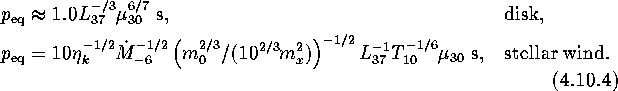
Let us turn to the case of disk accretion.  The above model of the spin-up and spin-down torques  possesses an unexpected property. The equilibrium period  obtained by setting the torque to zero is connected with the critical period through a dimensionless factor:

The parameters and must be such that . Since , the equilibrium period in the case of disk accretion is close to the critical period, , separating accretion stage A and the propeller stage P. In the case of the supercritical accretion  the equilibrium period is determined by formula (Lipunov, 1982b[99])