Next: Ejector-propeller hysteresis Up: Evolution of Magnetic Rotators Previous: Evolution of Magnetic Rotators
![]()
![]()
![]()
![]()
![]()
Next: Ejector-propeller
hysteresis Up: Evolution
of Magnetic Rotators Previous: Evolution
of Magnetic Rotators
The impact of eccentricity on the observed properties of X-ray pulsars
has been considered in many papers (Guseinov, 1971[63];
Shakura and Sunyaev, 1973[177];
Pacini and Shapiro, 1975[149];
Lipunov and Shakura, 1976[109]).
The most important consequence of orbital eccentricity for the evolution
of rotators can be understood without detailed calculations, and suggests
the existence of two different types of binary systems separated by a critical
eccentricity, ![]() (Gnusareva and Lipunov, 1985)[56]).
(Gnusareva and Lipunov, 1985)[56]).
Consider an ideal situation when a rotator enters a binary system with
some eccentricity. The normal star (no matter how) supplies matter to the
compact magnetized rotator. We assume that all the parameters of the binary
system (binary separation, eccentricity, masses, accretion rate, etc.)
are stationary and unchanged. Then a critical eccentricity ![]() appears such that at
appears such that at ![]() the rotator is not able to reach the accretion state in principle. Let
the rotator be rapid enough initially to be at the ejector (E)
state. With other parameters constant, the evolution of such a star is
determined only by its spindown. The star will gradually
spindown to such a state that when passing close to the periastron where
the density of the surrounding matter is higher, the pulsar will ``choke''
with plasma and pass into the propeller regime. Therefore,
for a small part of its life the rotator will be in a mixed EP-state, being
in the propeller state at periastron and at the ejector state close to
apastron. The subsequent spindown of the rotator leads most probably to
the propeller state along the entire orbit. This is due to the fact that
the pressure of matter penetrating the light cylinder
the rotator is not able to reach the accretion state in principle. Let
the rotator be rapid enough initially to be at the ejector (E)
state. With other parameters constant, the evolution of such a star is
determined only by its spindown. The star will gradually
spindown to such a state that when passing close to the periastron where
the density of the surrounding matter is higher, the pulsar will ``choke''
with plasma and pass into the propeller regime. Therefore,
for a small part of its life the rotator will be in a mixed EP-state, being
in the propeller state at periastron and at the ejector state close to
apastron. The subsequent spindown of the rotator leads most probably to
the propeller state along the entire orbit. This is due to the fact that
the pressure of matter penetrating the light cylinder ![]() increases faster than that caused by relativistic wind and radiation, as
first noted by Schwartzman (1971)[176].
So it proves to be much harder for the rotator to pass from the P state
to the E state than from E to P state (see the following section).
increases faster than that caused by relativistic wind and radiation, as
first noted by Schwartzman (1971)[176].
So it proves to be much harder for the rotator to pass from the P state
to the E state than from E to P state (see the following section).
The rotator will spindown ultimately to some period,
![]() , at which accretion will be possible during the periastron passage. Accretion,
in contrast, will lead to a spin-up of the rotator,
so that it reaches some average equilibrium state characterized by an equilibrium
period
, at which accretion will be possible during the periastron passage. Accretion,
in contrast, will lead to a spin-up of the rotator,
so that it reaches some average equilibrium state characterized by an equilibrium
period ![]() defined by the balance of accelerating and decelerating
torques averaged over the orbital period. If the eccentricity were zero,
the rotator would be in the accretion state all the time. By increasing
the eccentricity and keeping the periastron separation between the stars
unchanged, we increase the contribution of the decelerating torque over
the orbital period and thus decrease
defined by the balance of accelerating and decelerating
torques averaged over the orbital period. If the eccentricity were zero,
the rotator would be in the accretion state all the time. By increasing
the eccentricity and keeping the periastron separation between the stars
unchanged, we increase the contribution of the decelerating torque over
the orbital period and thus decrease ![]() . At some ultimate large enough eccentricity
. At some ultimate large enough eccentricity ![]() the equilibrium period will be less than the critical period
the equilibrium period will be less than the critical period ![]() permitting the transition from the propeller state to the accretion state
at apastron to occur. The rotational torque applied to the rotator, averaged
over orbital period, vanishes, and in this sense the equilibrium state
is achieved, but the rotator periodically passes from the propeller state
to the accretion state.
permitting the transition from the propeller state to the accretion state
at apastron to occur. The rotational torque applied to the rotator, averaged
over orbital period, vanishes, and in this sense the equilibrium state
is achieved, but the rotator periodically passes from the propeller state
to the accretion state.
Thus, X-ray pulsars with unreachable full-orbit accretion state must exist. This means that from the observational point of view such binaries will be observed as transient X-ray sources with stationary parameters for the normal component.
Typically, the evolutionary track of a rotator in an eccentric binary is
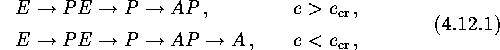
this may be a principal means of transient X-ray source formation.