As mentioned earlier, the transition of the rotator from the ejector
state to the propeller state is not symmetrical. Here we consider this
effect in more detail. In terms of our approach, we must study the
dependence of ![]() on
on ![]() . To find
. To find ![]() , we
must match the ram pressure of the accreting plasma with that caused by
the relativistic wind or by the magnetosphere of the rotator (see
Section 4.3). This dependence
, we
must match the ram pressure of the accreting plasma with that caused by
the relativistic wind or by the magnetosphere of the rotator (see
Section 4.3). This dependence ![]() will
be substantially different for rapidly (
will
be substantially different for rapidly ( ![]() ) and slowly
(
) and slowly
( ![]() ) rotating stars (see Figure 12). One can see
that in the case of a fast rotator, an interval of
) rotating stars (see Figure 12). One can see
that in the case of a fast rotator, an interval of ![]() appears
where three different values of
appears
where three different values of ![]() are possible, the upper value
are possible, the upper value
![]() corresponding to the ejector state and the bottom value
corresponding to the ejector state and the bottom value ![]() to
the propeller state; the intermediate value
to
the propeller state; the intermediate value ![]() is unstable. This
means that the rotator's state is not determined solely by the value of
is unstable. This
means that the rotator's state is not determined solely by the value of
![]() , but also depends on previous behavior of
, but also depends on previous behavior of ![]() .
.
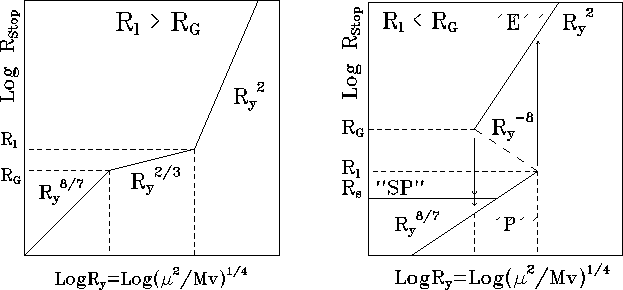
Figure 12: Dependence of the stopping radius
![]() on the modified gravimagnetic radius
on the modified gravimagnetic radius ![]() for two possible relations between the light cylinder radius
for two possible relations between the light cylinder radius
![]() and the gravitation capture radius
and the gravitation capture radius ![]() :
: ![]() (left-hand
panel) and
(left-hand
panel) and ![]() (right-hand panel; here the ejector-propeller hysteresis
becomes possible).
(right-hand panel; here the ejector-propeller hysteresis
becomes possible).
Now consider a periodic changing of ![]() caused, for example, by
the rotator's motion along an eccentric orbit, and large enough for the
rotator to transit from the ejector state
to the propeller state and
vice versa. Initially, the rotator is in the ejector state. By
approaching the normal star, the accretion rate
caused, for example, by
the rotator's motion along an eccentric orbit, and large enough for the
rotator to transit from the ejector state
to the propeller state and
vice versa. Initially, the rotator is in the ejector state. By
approaching the normal star, the accretion rate ![]() increases
and reaches a critical value
increases
and reaches a critical value ![]() , where the equilibrium
points
, where the equilibrium
points ![]() (stable point corresponding to the ejector state) and
(stable point corresponding to the ejector state) and
![]() (unstable) approach
(unstable) approach ![]() (upper kink), where they merge (see
Figure 12).
After that
only one equilibrium point remains in the system, the stopping radius
(upper kink), where they merge (see
Figure 12).
After that
only one equilibrium point remains in the system, the stopping radius
![]() jumps from
jumps from ![]()
![]() down to
down to ![]() , and the
rotator changes to the propeller state.
, and the
rotator changes to the propeller state.
As ![]() decreases further along the orbit and reaches
the critical value
decreases further along the orbit and reaches
the critical value ![]() once again,
the reverse transition from propeller to ejector does not occur.
The transition only occurs when
once again,
the reverse transition from propeller to ejector does not occur.
The transition only occurs when ![]() reaches another critical value,
reaches another critical value, ![]() where the unstable point
where the unstable point ![]() meets the stable propeller point
meets the stable propeller point ![]() ,
and the stopping radius
,
and the stopping radius ![]() jumps from
jumps from ![]()
![]() up to
up to
![]() .
.
It should be noted that for fast enough rotators, a situation is
possible when the step down from the ejector state occurs in such a
manner that the stopping radius ![]() and the rotator passes
directly to the accretion state.
The reverse transition always passes
through the propeller stage:
and the rotator passes
directly to the accretion state.
The reverse transition always passes
through the propeller stage: ![]() . In
principle, transitions from the ejector state to supercritical states
SP or SA are also possible (Prokhorov, 1987a; Osminkin and Prokhorov,
1995)[166, 147].
In the case of slow rotators
(
. In
principle, transitions from the ejector state to supercritical states
SP or SA are also possible (Prokhorov, 1987a; Osminkin and Prokhorov,
1995)[166, 147].
In the case of slow rotators
( ![]() ), the ``E-P'' hysteresis is not possible, and transitions
between these states are symmetrical.
), the ``E-P'' hysteresis is not possible, and transitions
between these states are symmetrical.