Next: A Gravitational Wave Map Previous: Critical Frequencies and Gravitational
Next: A
Gravitational Wave Map Previous: Critical
Frequencies and Gravitational
In this section we consider the GWB spectrum as such, that is, we study
how dimensionless strain metric amplitude h
is dependent on frequency. For a sample of N
independent binaries emitting GW at a given frequency 
the net result is
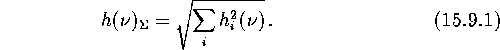
If one uses the frequency interval 
, the result will be
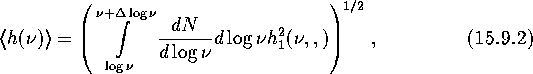
where
is the familiar amplitude produced by an individual binary,
are, respectively, effective distance to the sample and effective mass
of the binaries (in solar units) producing the GW radiation at the frequency
. For example, for a homogeneous sample (which is a good approximation
to extragalactic binaries) one obtains 
, where 
is the outer boundary of the sample.
Making use of expressions (15.3.2), (15.3.3) and (15.9.3) yields
for the red end of the spectrum ( 
) and
for the blue end.
One may be interested in how the GWB from the external object relates
to that from our Galaxy, providing that the observations are being performed
with a detector of angular resolution 
such that the Galaxy is still not transparent at the frequency of observations,
and the object is inside the detector's beam, 
. In this case
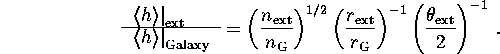
Here n is the number of stars within the object, 
is an effective ``radius'' of the Galaxy 
kpc. Some specific examples are shown in Table 13.
It can be seen from Table 
that only the closest stellar systems (such as Magellanic Clouds
and M31) can noticeably affect the galactic binary background. The level
of the cosmological binary GWB is always an order of magnitude below the
galactic level. Indeed, in analogy with expressions (15.9.4)
and (15.9.5) one obtains for the red (flat)
and blue (decreasing) parts of the spectrum, respectively: $$ .h|_r =2.1
10^-17 n_11^1/2N_11^1/2^2/3 C_4/3^1/2(3500 Mpcr),
Their comparison with expressions (15.9.4) and (15.9.5) yields
for both ends of the spectrum.
The GW noise produced by extragalactic binary systems
is still considerably higher than the expected amplitudes of relic gravitational
waves produced in well-known inflationary models (Rubakov et al.,
1982[169]): 
,
even if one conducts observations at the galactic poles which are poor
in stars.
Figure 43: Distribution of galaxies from Tully's Catalog by distance.
