Next: Results and Discussion Up: Evolution of Supernova Explosion Previous: - Dependence for the
![]()
![]()
![]()
![]()
![]()
Next: Results
and Discussion Up: Evolution
of Supernova Explosion Previous: -
Dependence for the
In order to construct the ![]() -
- ![]() dependence for supernova explosions, we calculated separately the m(z)
in the R band and N(z)
taking the cosmological and evolutionary effects into account. Thus we
get
dependence for supernova explosions, we calculated separately the m(z)
in the R band and N(z)
taking the cosmological and evolutionary effects into account. Thus we
get
![]()
where ![]() is the
photometric distance
is the
photometric distance
![]()
and ![]() is the spectral
correction
is the spectral
correction
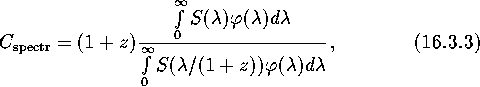
where ![]() is the
spectral distribution of the energy flux from a supernova and
is the
spectral distribution of the energy flux from a supernova and ![]() is the filter transmission function.
is the filter transmission function.
We have not taken extinction (both inside galaxies and en routeto Earth) into account, although of course it will affect the observed m(z) and N(z). It is especially important for SN of type II because they are usually located in star-forming regions rich in dust and gas; this may considerably alter the observed magnitude and even make detection impossible.
We calculate the ![]() dependence for supernovae at the maximum brightness, assuming the SN spectrum
to be black body with a temperature
dependence for supernovae at the maximum brightness, assuming the SN spectrum
to be black body with a temperature ![]() K for SN Ia,
K for SN Ia, ![]() K for SN II and SN Ib, and M(R) at maximum be -18.9, -17.3 and -16.3 for
SN Ia, SN Ib and SN II, respectively (van den Bergh and Tammann, 1991)[200].
The Hubble constant was taken to be H=75 km
s
K for SN II and SN Ib, and M(R) at maximum be -18.9, -17.3 and -16.3 for
SN Ia, SN Ib and SN II, respectively (van den Bergh and Tammann, 1991)[200].
The Hubble constant was taken to be H=75 km
s![]() Mpc
Mpc![]() .
.
Although the observed ultraviolet spectra of SN I is much weaker than
the approximated black body law, we can still use this approximation for
the R band up to the redshifts of ![]() , where
, where ![]() is the
characteristic wavelength of the ultraviolet ``drop'' in the spectra. For
larger z, the effect of the ultraviolet emission
suppression in SN I spectra would result in an almost complete lack of
SN I fainter than some limit. The dependence of m on z is displayed in
Figure 52.
is the
characteristic wavelength of the ultraviolet ``drop'' in the spectra. For
larger z, the effect of the ultraviolet emission
suppression in SN I spectra would result in an almost complete lack of
SN I fainter than some limit. The dependence of m on z is displayed in
Figure 52.
The number of SN per unit time within the sphere of redshift less than z is
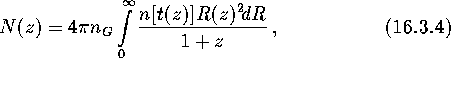
where n(t) is the SN rate as a function
of age of the galaxy, t(z) is the age of the
galaxy as a function of its redshift, and ![]() is the density of galaxies in the Universe. We assumed
is the density of galaxies in the Universe. We assumed ![]() Mpc
Mpc![]() , which corresponds to the fractional density of stars relative to the
critical density
, which corresponds to the fractional density of stars relative to the
critical density ![]() .
.
We use a conventional cosmological model of a flat Universe without
cosmological constant ![]() (
( ![]() ,
, ![]() ). In this case,
). In this case,
![]()
and
![]()
where c is the velocity of light, and ![]() is the redshift of the initial star formation.
is the redshift of the initial star formation.
We assumed that the SN spectrum and luminosity are both independent
of the age of the galaxy, and that the SN rate evolution n(t)
significantly influences the ![]() -
- ![]() law.
law.