<< 4.1 Прохождение света через | Оглавление | 4.3 Рассеяние на аэрозолях >>

4.2 Ослабление света релеевским (молекулярным) рассеянием

Молекулярные флуктуации плотности воздуха вызывают рассеяние световой волны. Часть света продолжает распространяться в прежнем направлении, а часть -- распределяется с различной интенсивностью под всеми углами к этому первоначальному направлению (причем часть света рассеивается назад). Функция зависимости интенсивности рассеянного света от угла рассеяния (т.е. от угла между направлением рассеяния и первоначальным направлением) называется индикатрисой рассеяния.

Формула для индикатрисы рассеяния в случае, когда размеры рассеивающих частиц малы по сравнению с длиной волны света, была впервые получена Релеем (Rayleigh). Из этой формулы, несколько видоизмененной в результате дальнейшего уточнения теории рассеяния (с учетом анизотропии молекул) следует, что поперечное сечение рассеяния $\sigma_R$, рассчитанное на одну молекулу равно

\begin{displaymath} \sigma_R(\lambda) = \frac{8\pi^3(n^2-1)^2}{3N^2\lambda_{\circ}^4}\, \frac{6+3d}{6-7d} , \end{displaymath} (4.7)

здесь $n$ - показатель преломления воздуха, $N$ - число молекул в 1см${}^3$ (число Лошмита). При нормальных условиях ($t$ = +15${}^{\circ}C$, $p=1013.25$мбар), $N$ = 2.687$\cdot$10${}^{-19}$ см${}^{-3}$. Второй сомножитель формулы включает величину $d$, которая для атмосферного воздуха равна 0.035. Это так называемый фактор деполяризации молекул.

Поскольку $n\approx1$ и $n^2-1\approx2(n-1)$, то, учитывая, что член с фактором деполяризации для воздуха равен 1.061, формулу 4.7 можно записать так:

\begin{displaymath} \sigma_R(\lambda) = 1.061\, \frac{32\pi^3(n^2-1)^2}{3N^2\lambda_{\circ}^4}. \end{displaymath} (4.8)

Чтобы получить значение оптической толщи $\tau_R$, обусловленной релеевским рассеянием, для всей атмосферы при наблюдении с высоты $h$ над уровнем моря, нужно поперечное сечение рассеяния умножить на количество частиц на пути луча в воздухе:

\begin{displaymath} \tau_R(\lambda,h) = \sigma_R (\lambda) \int \limits_{h}^{\i... ...N(h,T)\,dh = \int \limits_{h}^{\infty} \beta_R(\lambda)\,dh , \end{displaymath} (4.9)

здесь $T$ - температура воздуха, а $\beta_R = \sigma(\lambda)N(h,T)$ - объемный (экспоненциальный) показатель ослабления света в воздухе:
\begin{displaymath} \beta_R(\lambda) = \frac{8\pi^3(n^2-1)^2}{3N\lambda_{\circ}^4}\, \frac{6+3d}{6-7d} . \end{displaymath} (4.10)

Следует обратить внимание на то, что показатель ослабления обратно пропорционален четвертой степени длины волны. Отсюда следует, что рассеяние коротковолнового излучения происходит существенно более интенсивно, чем длинноволнового. Именно этим голубым рассеянным светом объясняется цвет дневного неба. При фотометрических измерениях видно, что и ночное небо, подсвеченное Луной, также имеет голубой оттенок: измерения фона неба при наличии Луны показывают, что наибольший фон мы имеем в синих спектральных полосах. Может показаться странным, что количество молекул в единице объема $N$ стоит в формуле в знаменателе. Это следствие того, что величина $n-1$ пропорциональна $N$ и в итоге $\beta_R(\lambda)$ пропорционально $N$, а не $1/N$. В формуле имеется еще небольшая неявная зависимость от длины волны, так как показатель преломления воздуха $n$, строго говоря, является функцией $\lambda$.

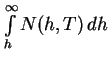При грубых оценках величину интеграла $\int \limits_{h}^{\infty} N(h,T)\,dh$ в формуле (4.9) заменяют высотой однородной атмосферы. Это условная атмосфера, в которой с высотой плотность воздуха не меняется, а давление при ее основании равно давлению при основании соответствующего столба воздуха в реальной атмосфере. При замене предполагается, что число молекул, определяемое интегралом в формуле (4.9), равно их числу в столбе однородной атмосферы. Высота однородной атмосферы вычисляется по формуле

\begin{displaymath} H(h)=H(0)\,p(h)/p(0), \end{displaymath} (4.11)

где $H(0)$ - высота однородной атмосферы на уровне моря, а $p(h)/p(0)$ - отношение давления воздуха на высоте $h$ к давлению на уровне моря. К сожалению, такая оценка довольно груба, так как высота однородной атмосферы на уровне моря заметно зависит от температуры: изменяется почти на 12% при изменении температуры от $-15^{\circ}C$ до $+15^{\circ}C$. При самых точных вычислениях по формуле (4.7) учитывают также зависимости показателя преломления воздуха от влажности и давления. Эти формулы можно найти, например, в справочнике К.У.Аллена ``Астрофизические величины'' (М.: Мир, 1977).

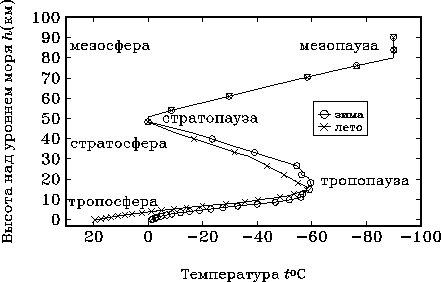
Распределения влажности, давления и температуры с высотой над уровнем моря в реальной атмосфере являются довольно сложными. Особенно это относится к температуре, стандартный ход которой с высотой показан на рис.4.2.

Рис. 4.2: Распределение средней температуры в атмосфере Земли с высотой над уровнем моря для летнего и зимнего сезонов
\begin{figure}\begin{center} \epsfxsize =0.8\textwidth\epsfbox{lfig4_2.eps}\end{center}\end{figure}

Вначале, в тропосфере, температура почти линейно падает с высотой. В районе тропопаузы (около 10 км) она постоянна и равна приблизительно $-55^{\circ}C$. Далее, в стратосфере, температура начинает расти и в стратопаузе вновь постоянна и приблизительно равна $0^{\circ}C$. А затем температура вновь начинает падать и достигает $-90^{\circ}C$ в мезопаузе.

Неучет влияния распределения температуры воздуха, давления и влажности с высотой на величину показателя преломления может дать ошибку (по крайней мере в несколько десятых долей процента), которую уже следует учитывать, если вы хотите достичь точности, сравнимой с аппаратурной точностью современных фотометров.

В последние годы на основе новых экспериментов уточнялась зависимость показателя преломления от длины волны. С учетом этих данных была получена аппроксимация значений $\sigma(\lambda)$:

(4.12)

где $x = 0.389\lambda + 0.09426/\lambda - 0.3228$ для 0.2$<\lambda<$0.55 мкм и x = 0.04 для 0.55$<\lambda<$1 мкм. Погрешность аппроксимации составляет около 0.5%. Если вычислен интеграл в формуле (4.9) или принято приближение однородной атмосферы, то спектральное пропускание атмосферы, ослабляющей свет за счет релеевского рассеяния, равно
\begin{displaymath} p_R(\lambda)=e^{-\tau_R(\lambda,h)} \end{displaymath} (4.13)

или в звездных величинах
\begin{displaymath} \Delta m_R(\lambda) = -2.5\,\lg p_R(\lambda) \approx -1.086\,\tau_R(\lambda,h). \end{displaymath} (4.14)

Вид функции $p_R(\lambda)$ показан на рис.4.3.

Рис. 4.3: Релеевское ослабление света
\begin{figure}\begin{center} \epsfxsize =0.8\textwidth\epsfbox{lfig4_3.eps}\end{center}\end{figure}

Это плавная кривая. В коротковолновой области ослабление составляет более одной величины, тогда как ослаблением в длинноволновой для некоторых приложений можно даже пренебречь: оно составляет 2-3%.


<< 4.1 Прохождение света через | Оглавление | 4.3 Рассеяние на аэрозолях >>