<< C. Вычисление интегралов
| Оглавление |
Литература >>
В данном приложении будет рассмотрена задача о поиске
аналитического решения для уравнений движения ядра кометы (первая
пара системы (50)). Рассмотрим второе
уравнение системы (50)
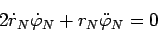 |
(78) |
Произведем замену переменных вида
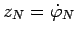 . Тогда
(78) можно переписать в виде:
. Тогда
(78) можно переписать в виде:
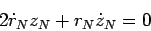 |
(79) |
откуда
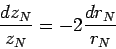 |
(80) |
Интегрируя последнее выражение, получаем
или
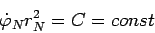 |
(81) |
здесь 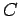 - постоянная площадей (удвоенная секторная скорость)
[2].
- постоянная площадей (удвоенная секторная скорость)
[2].
Следовательно, первое уравнение системы
(50) можно представить в виде:
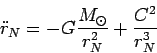 |
(82) |
Для решения последнего уравнения произведем замену переменных
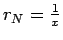 , тогда
, тогда
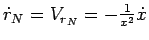 - радиальная составляющая скорости ядра (линейная
орбитальная скорость). В итоге (83) можно представить в
виде:
- радиальная составляющая скорости ядра (линейная
орбитальная скорость). В итоге (83) можно представить в
виде:
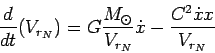 |
(83) |
Здесь учтено, что
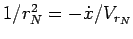 . Проинтегрируем
последнее соотношение.
. Проинтегрируем
последнее соотношение.
Откуда
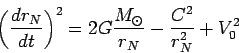 |
(84) |
иначе
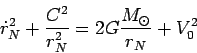 |
(85) |
где 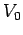 - постоянная интегрирования. Учтем также, что
- постоянная интегрирования. Учтем также, что
следовательно
откуда
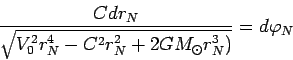 |
(86) |
Проинтегрируем (87)
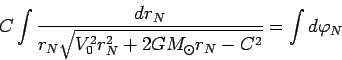 |
(87) |
Произведем замену переменных вида 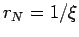 , тогда
, тогда
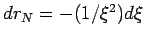 , следовательно (88) можно
представить в виде:
, следовательно (88) можно
представить в виде:
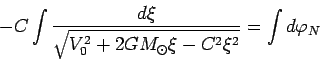 |
(88) |
Произведем замену переменных вида
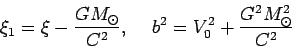 |
(89) |
следовательно, (89) можно представить в виде:
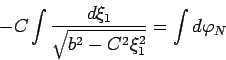 |
(90) |
произведем в (91) замену следующего вида
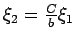 , тогда последнее выражение может быть
представлено в виде:
, тогда последнее выражение может быть
представлено в виде:
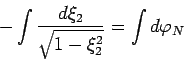 |
(91) |
откуда получаем
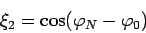 |
(92) |
Вернемся к исходной переменной 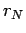 , тогда (93)
можно представить в виде:
, тогда (93)
можно представить в виде:
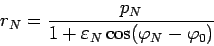 |
(93) |
где
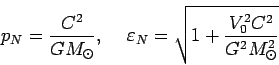 |
(94) |
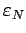 - эксцентриситет орбиты. Если направление на
афелий взять за начальное направление радиуса-вектора, то
постоянная интегрирования
- эксцентриситет орбиты. Если направление на
афелий взять за начальное направление радиуса-вектора, то
постоянная интегрирования 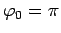 и уравнение орбиты
принимает вид:
и уравнение орбиты
принимает вид:
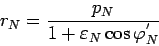 |
(95) |
где
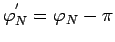 . Следовательно, выражение
(86) в терминах новых параметров может быть
представлено в виде:
. Следовательно, выражение
(86) в терминах новых параметров может быть
представлено в виде:
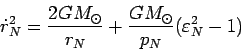 |
(96) |
учитывая определение большой полуоси орбиты ядра 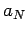 :
:
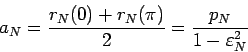 |
(97) |
выражение (97) можно переписать в виде:
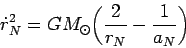 |
(98) |
Подставляя 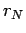 из (96) в (82) и интегрируя,
получаем
из (96) в (82) и интегрируя,
получаем
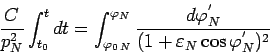 |
(99) |
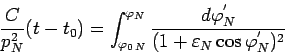 |
(100) |
Ситуация 1: Параболическая орбита
(
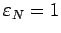 ).
).
Тогда после интегрирования в правой части (101) и
учитывая, что 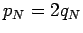 , где
, где 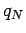 - перигелийное расстояние
ядра, будем иметь:
- перигелийное расстояние
ядра, будем иметь:
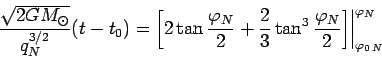 |
(101) |
Принимая за начало шкалы времени момент времени, когда ядро
находится в афелии (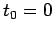 ), то получаем:
), то получаем:
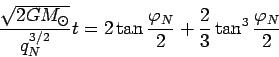 |
(102) |
Решая последнее уравнение относительно 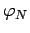 , получаем
зависимость
, получаем
зависимость
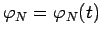 . Подставляя последнее
выражение в (96), получаем явную зависимость
. Подставляя последнее
выражение в (96), получаем явную зависимость
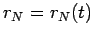 . Таким образом, найден закон движения ядра кометы,
движущегося по параболической орбите.
. Таким образом, найден закон движения ядра кометы,
движущегося по параболической орбите.
Ситуация 2: Эллиптическая орбита
(
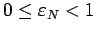 ).
).
В данном случае непосредственное интегрирование (101)
затруднительно. В этом случае удобно ввести вспомогательный угол
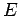 - эксцентрическую аномалию и выразить
- эксцентрическую аномалию и выразить 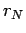 ,
, 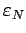 в
функции этого угла (смотри рис. 27).
в
функции этого угла (смотри рис. 27).
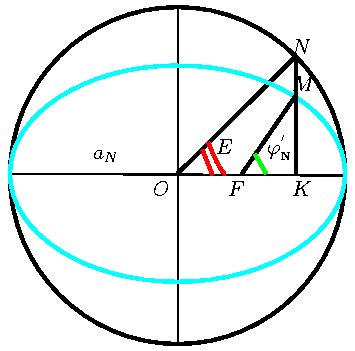
|
| Рис. 27.
К определению угла E.
|
На большой оси как на диаметре строим окружность. Проводим через
положение ядра кометы (точка 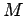 ) перпендикуляр
) перпендикуляр 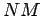 к большой оси
орбиты до пересечения с окружностью. Угол
к большой оси
орбиты до пересечения с окружностью. Угол 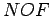 и есть
эксцентрическая аномалия
и есть
эксцентрическая аномалия 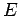 . Очевидно, что
. Очевидно, что 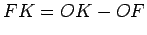 или
или
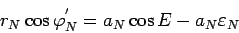 |
(103) |
Здесь по-прежнему
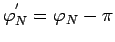 . С другой стороны
(96) можно представить в виде:
. С другой стороны
(96) можно представить в виде:
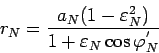 |
(104) |
или
Подставляя значение
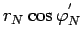 из
(104), получаем
из
(104), получаем
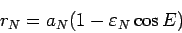 |
(105) |
Исключая из (105) и (106) переменную
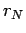 , имеем
, имеем
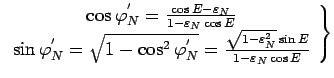 |
|
|
(106) |
(перед корнем берем знак "+", поскольку
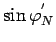 имеет
тот же знак, что и
имеет
тот же знак, что и 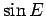 ). Остается найти зависимость
). Остается найти зависимость 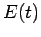 .
Заметим, что на основании (107)
.
Заметим, что на основании (107)
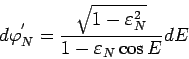 |
(107) |
Подставим значение
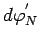 и выражение для
и выражение для 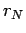 из
(106) в (82). В результате интегрирования
(82) получаем уравнение Кеплера.
из
(106) в (82). В результате интегрирования
(82) получаем уравнение Кеплера.
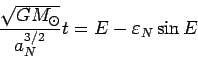 |
(108) |
Решая последнее уравнение относительно переменной 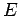 , получаем
зависимость
, получаем
зависимость 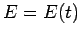 , а, следовательно, и закон движения ядра
кометы
, а, следовательно, и закон движения ядра
кометы
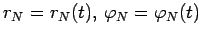 .
.
Ситуация 3: Гиперболическая
орбита (
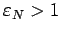 ).
).
В случае гиперболической орбиты ядра кометы
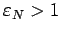 ,
,
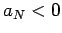 , а
, а
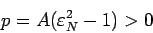 |
(109) |
где 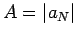 . Поэтому (96) принимает вид:
. Поэтому (96) принимает вид:
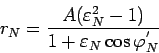 |
(110) |
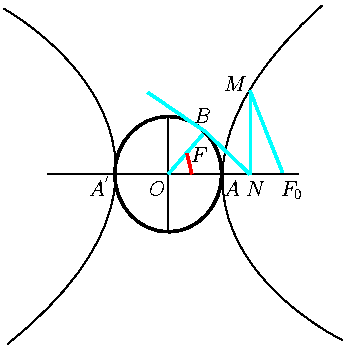
Для интегрирования (101) введем вспомогательный угол 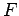 следующим образом. На оси гиперболы
следующим образом. На оси гиперболы 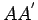 (смотри рис.
28), как на диаметре, строим окружность. Из
положения ядра кометы (точка
(смотри рис.
28), как на диаметре, строим окружность. Из
положения ядра кометы (точка 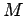 ) опускаем перпендикуляр
) опускаем перпендикуляр 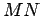 на
ось
на
ось 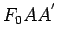 .
.
|
| Рис. 28.
К определению угла F.
|
Из 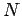 проводим касательную к окружности и через точку касания
проводим касательную к окружности и через точку касания 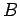 проводим прямую
проводим прямую 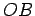 ; угол
; угол 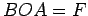 . Имеем
. Имеем 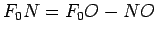 или
или
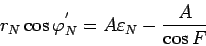 |
(111) |
Исключая
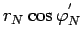 из (111) и
(112), получаем окончательно
из (111) и
(112), получаем окончательно
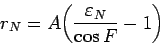 |
(112) |
Используя (111), получаем окончательно
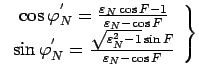 |
|
|
(113) |
на основании (114) имеем
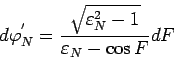 |
(114) |
Подставляя значение
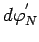 и выражение для
и выражение для 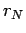 из
(115), (113) в (82), получаем
из
(115), (113) в (82), получаем
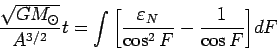 |
(115) |
и производя замену следующего вида
получаем окончательно
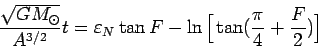 |
(116) |
Решая последнее уравнение относительно переменной 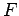 , получаем
зависимость
, получаем
зависимость 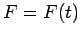 , а, следовательно, и закон движения ядра
кометы
, а, следовательно, и закон движения ядра
кометы
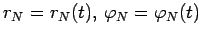 .
.
Таким образом, имея элементы орбиты кометы, можно всегда
определить ее закон движения.
<< C. Вычисление интегралов
| Оглавление |
Литература >>
![]() . Тогда
(78) можно переписать в виде:
. Тогда
(78) можно переписать в виде:
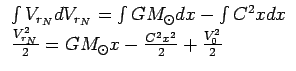
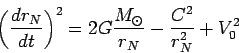
![]() - постоянная интегрирования. Учтем также, что
- постоянная интегрирования. Учтем также, что
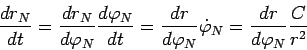
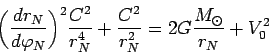
![]() , тогда
, тогда
![]() , следовательно (88) можно
представить в виде:
, следовательно (88) можно
представить в виде:
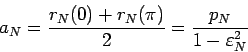
![]() ).
).
![]() , где
, где ![]() - перигелийное расстояние
ядра, будем иметь:
- перигелийное расстояние
ядра, будем иметь:
![]() ).
).
![]() - эксцентрическую аномалию и выразить
- эксцентрическую аномалию и выразить ![]() ,
, ![]() в
функции этого угла (смотри рис. 27).
в
функции этого угла (смотри рис. 27).
![]() ) перпендикуляр
) перпендикуляр ![]() к большой оси
орбиты до пересечения с окружностью. Угол
к большой оси
орбиты до пересечения с окружностью. Угол ![]() и есть
эксцентрическая аномалия
и есть
эксцентрическая аномалия ![]() . Очевидно, что
. Очевидно, что ![]() или
или
![]() ).
).
![]() ,
,
![]() , а
, а
![]() проводим касательную к окружности и через точку касания
проводим касательную к окружности и через точку касания ![]() проводим прямую
проводим прямую ![]() ; угол
; угол ![]() . Имеем
. Имеем ![]() или
или