<< B. Вычисление параметра ρ(θ) | Оглавление | D. Аналитическое решение ... >>

C. Вычисление интегралов I1, I2

В данном приложении будут представлены аналитические результаты для интегралов , , как функций показателя преломления. Итак, согласно выражению (16), интеграл имеет следующий вид.

(68)

Произведем замену переменных вида:
(69)

И, следовательно, (68) можно переписать так:
(70)

Произведем еще одну замену переменных
(71)

Заметим, что функция , согласно (64), (66), (67), зависит от , следовательно, производя замену (71) мы получаем функцию следующего вида:
(72)

C учетом (71) и (72), выражение (70) может быть представлено в виде:
(73)

Используя метод подстановок Эйлера для вычисления последнего интеграла, с помощью компьютерной математической системы [17], получаем следующий аналитический результат:

 
   
   
   
   
  (74)

Рассмотрим интеграл . Согласно (17), имеем

(75)

Вновь произведем замены переменных (69), (71); в результате представляется следующим выражением.
(76)

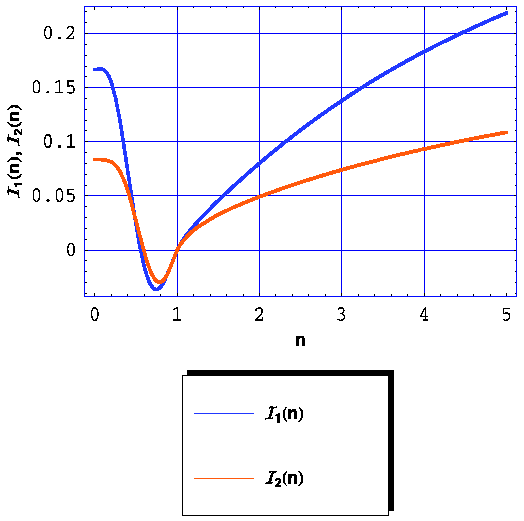
Рис. 26. Зависимость интегралов , от показателя преломления .

Вновь используя метод подстановок Эйлера (с помощью Mathematica 4.1), в результате получаем:

 
   
   
   
   
   
   
  (77)

В заключение приведем графики зависимостей , на интервале (смотри рис.26).


<< B. Вычисление параметра ρ(θ) | Оглавление | D. Аналитическое решение ... >>