В данном параграфе будет рассмотрена плоская
ограниченная задача трех тел (смотри 
2). Первым этапом
решения поставленной задачи является определение уравнений
движения системы "ядро кометы - частица". Вторым этапом является
определение начальных условий, однозначно определяющих законы
движения указанных тел. Этим этапам будет посвящен первый пункт
данного параграфа.
Второй пункт данного параграфа будет посвящен анализу законов движения тел модели на примере ядра кометы Галлея, предполагая, что вещество, слагающее частицу - водный лед.
Согласно определенной модели рассматриваемой
физической системы уравнения движения для ядра и частицы кометы
могут быть представлены системой (35)
или
Первые два уравнения системы (49) с
учетом начальных условий определяют закон движения ядра кометы.
Возможные аналитические решения для данной пары уравнений
представлены в приложении 
. Вторая пара уравнений системы
(49) определяет (с учетом начальных
условий) закон движения частицы ядра кометы. Очевидно, что
последняя пара уравнений системы (49)
может быть решена лишь совместно с первыми двумя уравнениями.
Учтем также, что
, а
параметр 
по-прежнему определяется выражением
(39). Следовательно, систему
(49) удобно представить в следующем
виде
Система дифференциальных уравнений
(50) есть система уравнений движения
плоской ограниченной задачи трех тел. Для однозначного решения
последней необходимо задать начальные условия. Будем полагать,
что в начальный момент времени ядро кометы и частица находятся в
афелии 8, т.е.
где
- угловая
скорость ядра кометы в афелии. Значение параметра 
будем определять непосредственно для каждого конкретного случая.
В данном пункте представим результаты и анализ законов движения ядра и частицы кометы Галлея. Отметим, что для численных расчетов значения фундаментальных констант, параметров орбиты кометы Галлея и ее массы были взяты из работ [6], [8], [10].
|
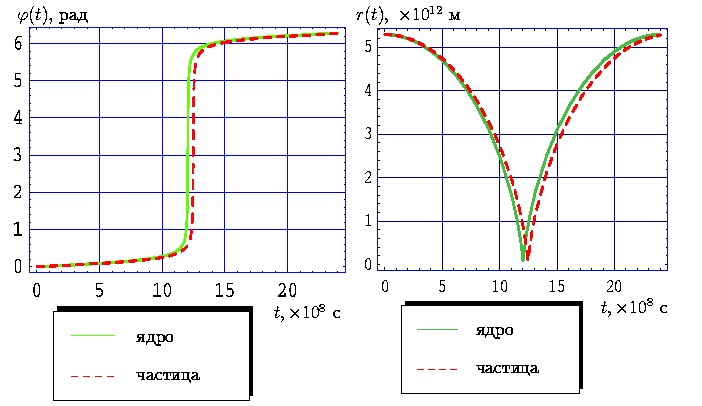
Рис. 13.
Законы движения ядра и частицы кометы Галлея с учетом
начальных условий (51) и
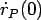 =0 м/с,
RP=10-5 м,
ρP=820 кг/м3,
nP=1.29 на временном интервале, равном одному
периоду обращения
(TГаллея=76 лет).
|
|
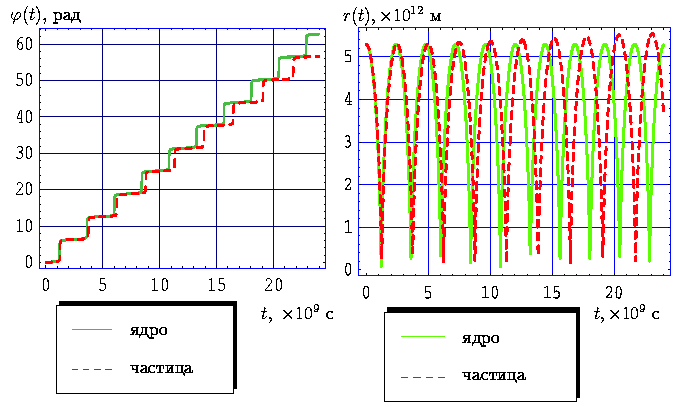
| Рис. 14.
Законы движения ядра и частицы кометы Галлея с учетом
начальных условий (51) и
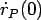=0 м/с,
RP=10-5 м,
ρP=820 кг/м3,
nP=1.29 на временном интервале, равном десяти
периоду обращения кометы.
|
|
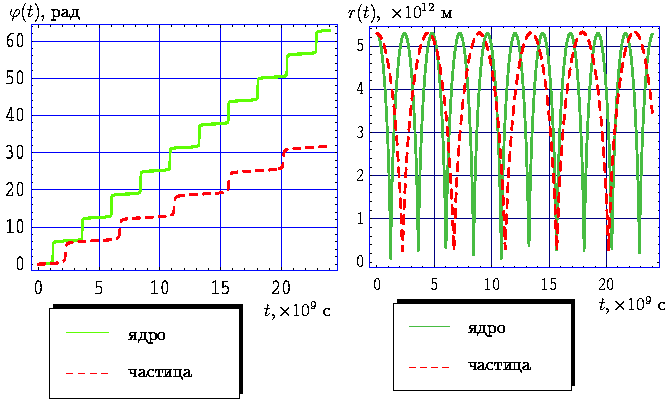
| Рис. 15.
Законы движения ядра и частицы кометы Галлея с учетом
начальных условий (51) и
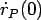=0 м/с,
RP=10-6 м,
ρP=820 кг/м3,
nP=1.29 на временном интервале, равном одному
периоду обращения кометы.
|
|
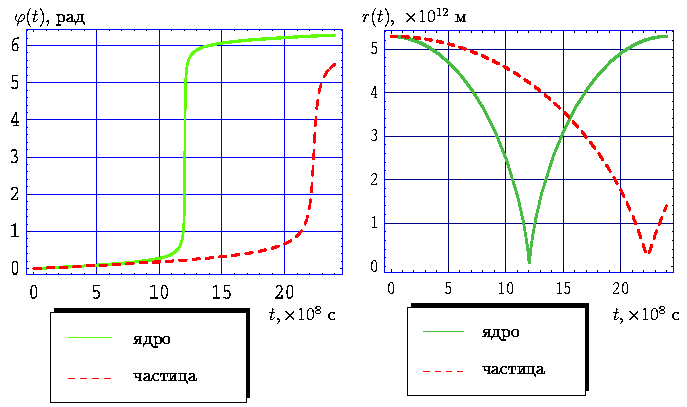
| Рис. 16.
Законы движения ядра и частицы кометы Галлея с учетом
начальных условий (51) и
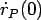=0 м/с,
RP=10-6 м,
ρP=820 кг/м3,
nP=1.29 на временном интервале, равном десяти
периоду обращения кометы.
|
|
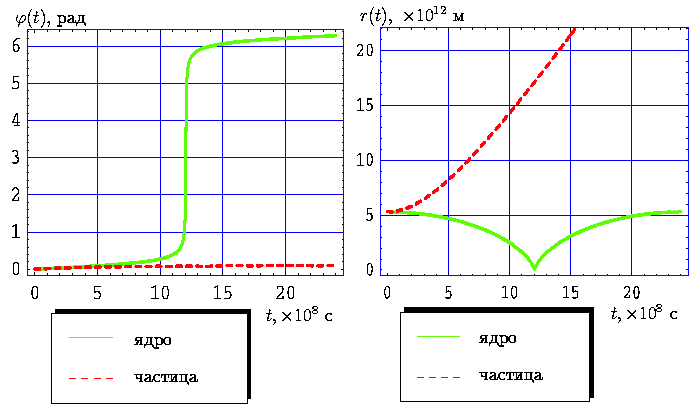
| Рис. 17.
Законы движения ядра и частицы кометы Галлея с учетом
начальных условий (51) и
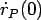=0 м/с,
RP=10-7 м,
ρP=820 кг/м3,
nP=1.29 на временном интервале, равном одному
периоду обращения кометы.
|
|
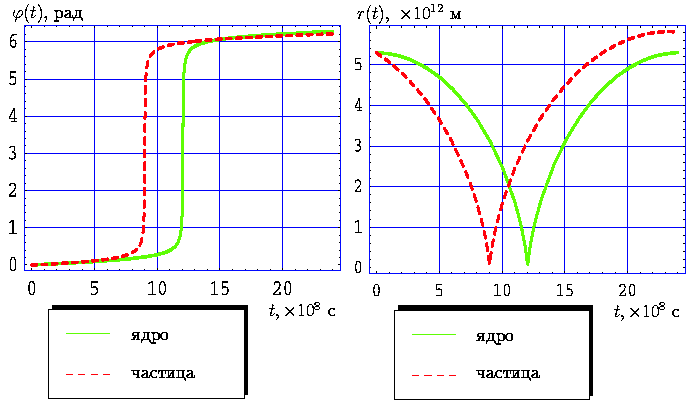
| Рис. 18.
Законы движения ядра и частицы кометы Галлея с учетом
начальных условий (51) и
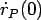=-2000 м/с,
RP=10-5 м,
ρP=820 кг/м3,
nP=1.29 на временном интервале, равном одному
периоду обращения кометы.Пример образования аномальных хвостов у
кометы.
|
На графиках 13 представлены законы движения ядра
кометы и частицы с радиусом RP=10-5 м
для
указанного набора начальных условий в случае временного интервала,
равного одному периоду обращения кометы Галлея
(RГаллея=76 лет).
Очевидно, что при проходе ядром кометы
перигелия частица весьма существенно отстает от ядра по значению
полярного угла, однако при этом величины радиусов-векторов этих
тел разнятся незначительно. Отсюда можно сделать вывод, что
данная частица (из водного льда) лежит на прямой, отклоняющейся на
значительный угол 
от направления "Солнце-ядро" (смотри
рис. 6), и, следовательно, участвует в образовании
кометного хвоста второго типа [1], [3].
На графиках 14 представлены законы движения ядра и частицы при тех же начальных условиях, что и в предыдущем случае, на временном интервале, равном десяти периодам обращения кометы. Очевидно, что по мере течения времени частица все более и более отстает от ядра кометы, и после шестого прохода перигелия кометой частица переходит на околосолнечную орбиту с периодом обращения, приблизительно равным 83 годам. При этом движение не является строго повторяющимся, поскольку с каждым оборотом афелий частицы удаляется от Солнца. Причина такого характера движения - существенное влияние силы светового давления на частицу при каждом проходе через перигелий.
На графиках 15 даны законы движения ядра кометы и частицы с радиусом RP=10-6 м для указанного набора начальных условий в случае временного интервала, равного одному периоду обращения кометы Галлея. Очевидно, что уже при первом проходе ядром кометы перигелия комета теряет частицу и последняя переходит на околосолнечную орбиту. При этом, очевидно, что роль силы светового давления в определении закона движения является более существенной, чем для частицы с радиусом RP=10-5 м (очень медленно меняется полярный угол).
Из графиков 16 (те же начальные условия, что и в предыдущем случае, на временном интервале, равном десяти периодам обращения кометы) становится ясно, что частица движется по околосолнечной орбите с периодом обращения, приблизительно равным 148.9 лет. И данное движение не является строго повторяющимся, поскольку афелий частицы удаляется от Солнца с каждым витком.
Демонстрация законов движения ядра и частицы с радиусом RP=10-7 м представлена на графиках 17 в случае временного интервала, равного одному периоду обращения кометы Галлея. Нетрудно видеть, что данный случай является подтверждением результатов, полученных в предыдущем параграфе. Здесь сила светового давления определяет характер движения частицы и радиус данной частицы меньше значения критического радиуса. Поэтому частица выбрасывается за пределы Солнечной системы.
На графиках 18 представлены законы движения ядра и частицы с RP=10-5 м в случае, когда в начальный момент времени частица выбрасывается из ядра кометы в направлении к Солнцу со скоростью 2 км/с. Очевидно, что при подходе к Солнцу частица движется впереди ядра. Она намного раньше проходит свой перигелий. Следовательно, такая частица может участвовать в образовании "аномальных" хвостов [1], [11], [12]. Ситуация такого извержения частиц из ядра может быть реализована при процессах деформации внутренних частей ядра, обусловленных изменением температуры среды, фазовыми переходами вещества ядра кометы.
Из рассмотренных результатов следует важный вывод: частица, потерянная кометой, может иметь два принципиально различных сценария движения. 1. Частица может быть захвачена Солнцем и перейти на околосолнечную орбиту, следовательно, кометы должны оставлять после себя "пояса" частиц, а точнее диск, который лежит в той же плоскости, что и орбита кометы, массовая плотность которого определяется количеством частиц, потерянных кометой, их радиусом, плотностью и их начальными условиями движения. 2. Частица может быть выброшена за пределы Солнечной системы, а, следовательно, стать частицей межзвездной среды. Если кометы образуются также в других звездных системах, то выброшенная в межзвездную среду кометная материя может являться одним из источников холодной темной материи (cold dark matter). Хотя ее вклад, скорее всего, будет очень малым в общую предполагаемую массу темной материи.
