Next: Special Cases: Supernova Explosion Up: Change of Binary Parameters: Previous: Mass change
![]()
![]()
![]()
![]()
![]()
Next: Special
Cases: Supernova Explosion Up: Change
of Binary Parameters: Previous: Mass
change
The binary separation a changes differently depending on the mass exchange mode. First, we introduce a measure of non-conservativeness of the mass exchange in the form of the ratio between the accreting and the mass-loosing star mass changes
![]()
If the mass transfer is conservative ( ![]() , i.e.
, i.e. ![]() const) and one may neglect the redistribution of the intrinsic angular
momenta of the components, the total orbital momentum conservation law
implies
const) and one may neglect the redistribution of the intrinsic angular
momenta of the components, the total orbital momentum conservation law
implies
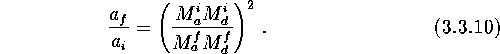
In a more general case of quasi-conservative mass transfer ![]() , the orbital separation changes depend on the specific angular momentum
removed from the system by the escaping matter (see detailed discussion
in van den Heuvel (1994)[205]). To be
specific, we use the ``isotropic mass loss mode'' by
letting matter remove the specific orbital angular momentum of the accreting
component (
, the orbital separation changes depend on the specific angular momentum
removed from the system by the escaping matter (see detailed discussion
in van den Heuvel (1994)[205]). To be
specific, we use the ``isotropic mass loss mode'' by
letting matter remove the specific orbital angular momentum of the accreting
component ( ![]() )
)
![]()
from which we straightforwardly find
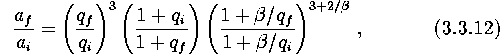
here ![]() .
.
If no matter is trapped by the secondary companion without additional sinks of angular momentum (the so-called absolutely non-conservative case), which relates to the spherically symmetric stellar wind from one component, we use another well-known formula
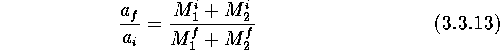
(the orbital separation always increases in such systems).
When the orbital angular momentum is removed by GR or MSW with no RL overflow, the following approximate formulas are used:
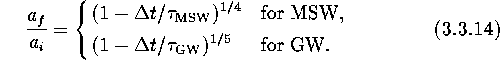
In a special case of a WD filling its RL (stage ``IIIwd'' above) under
assumption of a stable conservative mass transfer and taking into account
that ![]() , it can be shown that the orbital separation must increase
, it can be shown that the orbital separation must increase
![]()