Next: The Scenario Machine: Operational Up: Evolution of Magnetic Rotators Previous: Ejector-propeller hysteresis
![]()
![]()
![]()
![]()
![]()
Next: The
Scenario Machine: Operational Up: Evolution
of Magnetic Rotators Previous: Ejector-propeller
hysteresis
Orbital motion of the rotator around the normal companion in an eccentric
binary draws a horizontal line on the ![]() diagram, with the beginning at a point corresponding to
diagram, with the beginning at a point corresponding to ![]() , and the end at a point corresponding to
, and the end at a point corresponding to ![]() (here
(here ![]() and
and ![]() are the periasrton and apastron distances, respectively). The length of
this segment is determined by the eccentricity. Since
are the periasrton and apastron distances, respectively). The length of
this segment is determined by the eccentricity. Since ![]() , the rotator moves along this segment from left to right and back as it
revolves from the apastron to the periastron. At each successive orbital
period, this line slowly drifts up to larger periods. The evolution of
this system is thus determined by the order the critical lines on the diagram
are crossed by this ``line''. It is seen from the
, the rotator moves along this segment from left to right and back as it
revolves from the apastron to the periastron. At each successive orbital
period, this line slowly drifts up to larger periods. The evolution of
this system is thus determined by the order the critical lines on the diagram
are crossed by this ``line''. It is seen from the ![]() diagram that the regions with and without hysteresis are separated by a
certain value of the parameter
diagram that the regions with and without hysteresis are separated by a
certain value of the parameter ![]() . Since
. Since ![]() , four different situations are possible depending on the relationship
of the binary orbital separation a with critical value
, four different situations are possible depending on the relationship
of the binary orbital separation a with critical value ![]() , corresponding to
, corresponding to ![]() (Osminkin and Prokhorov, 1995[147];
see Figure 13 and corresponding cases
(a)-(d) below).
(Osminkin and Prokhorov, 1995[147];
see Figure 13 and corresponding cases
(a)-(d) below).
Figure 13: Possible variants of the ejector-propeller transitions
of a NS in an eccentric binary system. The NS rotational period spins down
from left to right. Four cases (a-d) correspond to different parameters
of binary systems: eccentricity, semi-axis and stellar wind
parameters as defined in the text. The hatched parts of the ellipses correspond
to propeller regime.
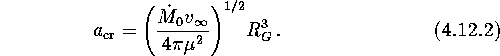
The value of ![]() can be expressed through the orbital parameters as
can be expressed through the orbital parameters as
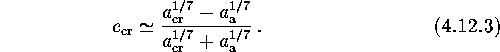
To conclude, we note that the hysteresis during the ejector-propeller
transition may be possible for single radiopulsars also.
For example, when the pulsar moves through a dense cloud of interstellar
plasma, the pulses can be absorbed. The radiopulsar turns on again when
it comes out from the cloud. The hysteresis amplitude for single pulsars
can be high enough because of small relative velocities of the interstellar
gas and the pulsar, so that ![]()