The Effect of Relativistic Ejectors in Massive Binary Why do Radiopulsars not

Caverns in Binary Systems

 

We follow the approach used by Lipunov and Prokhorov (1984)[110]. Suppose that a NS having a rotational magnetic  luminosity forms a binary system (with semi-major axis a) with a normal star losing matter in the form of stellar wind (with a loss rate ).

Let us find the Schwartzman radius  in accordance with the definition and by equating the plasma pressure to the electromagnetic pressure :

where R is the distance from the NS. The Schwartzman radius  is (see Lipunov and Prokhorov, 1984[110]; Harding, 1991[64]):

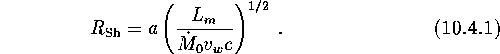
When making estimates, it is convenient to use the fact that the outflow rate, luminosity and the stellar wind velocity of hot stars are connected through the empirical relation (see, for example, Barlow and Cohen, 1977[8])

where -0.4. This leads to the approximation

 

The luminosity of normal stars whose mass varies from a few times to several tens of times the mass of the Sun lies in the interval between and - erg s . The rotational magnetic luminosity  of NS also varies in the same wide range. For ``aged'' radiopulsars, erg s , while for young pulsars may be as high as - erg s . Equation (10.4.3) shows that entirely different situations may arise in different binary systems at various stages of evolution. For example, or . This means that while deriving the formula for a cavern in the general case, we must take into account the proximity of the normal star.

 
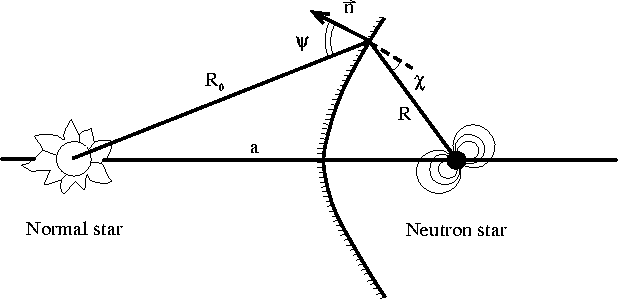
Figure 28: Schematic representation of a pulsar in a pair with a normal star. 

Let us calculate the shape of a cavern  surrounding a NS, assuming that the relativistic wind ejected by the star is spherically symmetric. We also assume that . At the cavern boundary (Figure 28), the following equilibrium condition must be satisfied:

 

where is the distance from the normal star, V is the volume of the cavern, and is the gas pressure. The second term on the right-hand side of the equilibrium equation (10.4.4) corresponds to the contribution of the pressure of the magnetic dipole radiation which is reflected back by the cavern ``walls'' and is accumulated inside it. The factor is zero for an open cavern and approximately 1 for a closed cavern. The static gas pressure can be presented in the form

For an isothermal stellar wind  (as a rule, this is the situation commonly encountered), n=0. We use dimensionless variables:

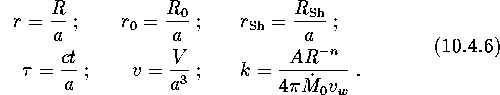
In this case, equation (10.4.4) becomes

Let us consider the case of an isothermal stellar wind (n=0) with no magnetic dipole radiation accumulated ():

It follows from the symmetry considerations that at the anterior point of the cavern (i.e. the point closest to the normal star), . This leads to the following expression for the distance from the anterior point:

Similarly, we can determine the distance from the posterior point of the cavern. We get

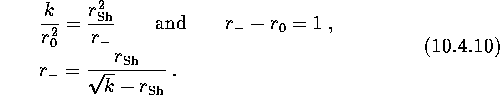
If , the cavern is closed. The value of k is of the order of the ratio of the square of the velocity of sound to the outflow rate of the stellar wind, so that in real situations - . Hence closed caverns must be quite compact: - . In most cases, the assumption k=0 may serve as a good approximation.

Only the electromagnetic waves with a frequency higher than the plasma frequency ( Hz) may propagate in a plasma. The characteristic density in the stellar wind is estimated from the continuity condition

where . Thus, the magnetic dipole radiation  should be reflected from the walls. Suppose that the reflection coefficient . In this case, the above analysis will remain valid if we redefine the Schwartzman radius as

This gives

It can be seen that the size of the cavern has increased. As , the cavern cannot remain stationary. It is either always open or pulsating quasi-periodically. In the latter case, the closed cavern expands right up to the maximum value :

The shape of the closed cavern is shown in Figure 29.

 
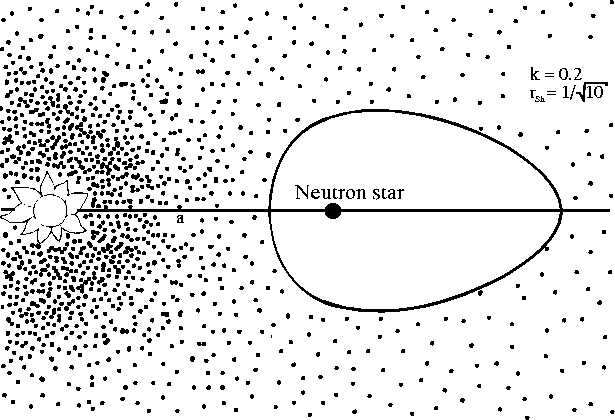
Figure 29: The cavern around a pulsar in a binary system (Lipunov and Prokhorov, 1984).[110]  

The Effect of Relativistic Ejectors in Massive Binary Why do Radiopulsars not