Next: The Radiopulsar PSRB1259-63 - a Up: Ejectors in Massive Binary Previous: Caverns in Binary Systems
Next: The
Radiopulsar PSRB1259-63 - a Up: Ejectors
in Massive Binary Previous: Caverns
in Binary Systems
Now let us try to take into account the rearrangement of the surrounding medium under the action of pulsar radiation in a similar way to how the stationary shells in the propeller regime are computed. Such an analysis, which was carried out by Davies and Pringle (1981)[39], is an extension of the model proposed by Gunn and Rees (1974)[62] for the Crab nebula.
Suppose that a cavern is formed around an ejecting star (for the sake
of simplicity, we assume that the cavern is spherical). We assume that
the entire energy 
emitted by the pulsar is dissipated at the internal wall of the cavern.
Obviously, the size of the cavern is of the order of the Schwartzman radius.
Near the inner boundary of the shell, the velocity of sound is equal to
the maximum possible value:
Since 
the pressure gradient is small and the pressure in the shell is constant.
Taking this into consideration, we obtain for the conservation of the energy
flux
The outer radius of the hot shell is determined from the condition 
:
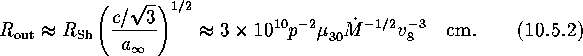
It follows from the second of the solutions (10.5.1)
that the ratio of the velocity of sound to the free-fall velocity is 
. Therefore, as the NS is spun down, 
becomes of the order of 
first at the outer boundary. Hence, Davies and Pringle proposed that the
shell collapses and the ejection stage is terminated when the inequality
is satisfied. This condition is equivalent to the following inequality
for the period:
If, however, the radius of the light cylinder is larger than the capture
radius, i.e. 
, the condition for the termination of the ejection stage remains valid.
Equation (10.5.3) can be used if
Thus, consideration of the inverse effect of pulsar radiation on the
properties of accreting plasma makes the ejection possible even when the
Schwartzman radius is smaller than the capture radius. It can be seen that
in this case the critical period estimation 
is not changed significantly. This is primarily due to the fact that the
power of a pulsar, and hence the pressure of the pulsar wind, depends very
strongly on its period (as 
). However, it remains unclear whether the shell will be stable when its
inner radius becomes smaller than the capture radius.
Lipunov and Prokhorov (1984)[110]
proposed a mechanism for the formation of radiobursts in the case 
which takes into account the possible contribution of pressure of the accumulated
magnetic dipole radiation. In this case, the process becomes time-dependent.
Let us assume that the magnetic dipole radiation reflected by the cavern
walls is stored inside and prevents the cavern from collapse. If the cavern
radius 
, the condition at its boundary can be written as
It can be seen that the pressure of the radiation in such a cavern rises
more rapidly (as 
) than the plasma pressure (which increases as 
). The cavern is filled up very quickly by radiation and begins to expand
(as 
). When its radius becomes equal to the capture radius, the gravitational
force is no longer important. The size of the cavern increases slightly,
it is detached from the NS and drifts upward with the stellar wind emanating
from the normal component. Apart from magnetic dipole radiation, the cavern
may also contain relativistic particles (which are also reflected from
the cavern boundary). Such caverns must produce very short radiopulses
when floating and bursting. The total energy and the characteristic radioburst
recurrence time can be easily estimated by using equation (10.5.5)
for 
. The energy of a radioburst is given by
The recurrence time 
and the duration 
of a burst are
For 
cm and 
- 
,
varies from a few hundred seconds to several weeks.
