Next: Why must a radiopulsar Up: Ejectors in Massive Binary Previous: The Effect of Relativistic
![]()
![]()
![]()
![]()
![]()
Next: Why
must a radiopulsar Up: Ejectors
in Massive Binary Previous: The
Effect of Relativistic
The discovery of this radiopulsar is potentially important not only for confirming the theory of evolution of NS, but also for understanding processes occurring in stellar winds from normal stars. After all, a radiopulsar orbiting in the semi-transparent stellar wind of a normal star is a sort of probe scanning an inhomogeneous plasma by pulsed radiation (Lipunov and Prokhorov, 1984)[110]. In this section, three periodic effects which could be observed in radiopulsars in binary systems are computed (see Lipunov et al., 1994a [123]):
1) absorption of radio waves (light curve);
2) variation of the pulse arrival time (dispersion measure curve); and
3) Faraday rotation of the polarization plane in the magnetic field of the stellar wind.
In our calculations, we do not take into account the refraction of radiowaves. In most cases this refraction can be neglected. However, in cases where it is significant, interesting details appear on the light curve of the radiopulsar (Lipunov and Prokhorov, 1987[115]).
Let us consider the system PSRB1259-63 in more detail. This object is a radiopulsar orbiting a Be-star. The pulsar was observed for nearly 1000 days at frequencies of 660 and 1520 MHz. At 430 MHz it was not seen. The time-dependence of the pulsar period and the light curve were obtained (see Figure 30).
Figure: The offset in the observed pulse period from 47.762 ms
and the light curve for PSRB1259-63 (Johnston et al., 1992).[78]
The dispersion measure (DM) remained constant
within the limits of the accuracy ( ![]() ) (Johnston et al., 1992[78],
1994[79]). From the arrival time
observations, a high orbital eccentricity and the following orbital parameters
have been obtained:
) (Johnston et al., 1992[78],
1994[79]). From the arrival time
observations, a high orbital eccentricity and the following orbital parameters
have been obtained:
![]()
The observations at two different frequencies give the same results. So, we can neglect dispersion fluctuations on the light curve and may consider the estimates of orbital parameters to be close to reality.
The pulsar was not seen in the interval between the 200th and 400th
day of observations ( ![]() ). This probably was due to occultation by a thick stellar wind near the
Be-star in the periastron (this explanation is in accordance
with the radial velocity curves).
). This probably was due to occultation by a thick stellar wind near the
Be-star in the periastron (this explanation is in accordance
with the radial velocity curves).
One can note some peculiarities of the light curve:
It should be emphasized here that because of the low relative accuracy of the observations, our confidence in the conclusions mentioned is rather small. The authors themselves neither spoke about nor interpreted these effects.
Johnston et al. (1992)[78] interpreted the main eclipse in terms of the model of a spherically symmetric stellar wind. In order to associate a strong absorption with a small change in dispersion measure, one has to consider the stellar wind matter to be clumped to a high degree (about 99 percent of concentration).
It may be suggested that for SS 2883, as well as for some other Be stars,
there is, besides the spherically symmetric stellar wind,
a disk-shaped outflow of matter in the equatorial plane of rotation of
the star. Wide emission lines, corresponding to a velocity of equatorial
rotation about 500 km s ![]() , may support this possibility (Johnston et al., 1992[78])
, may support this possibility (Johnston et al., 1992[78])
Let us consider now the simplest two-component model: stellar wind + equatorial disk:
In this model we can estimate the DM and the optical thickness
due to free-free scattering (proportional to the emission measure EM).
The location of the pulsar in the wind is determined by two parameters:
an impact parameter of the line of sight p (p>0) and the
distance from the pulsar to the point on this line closest to the center
of the optical star, z (z>0 when the pulsar is more distant
than the star, and z<0 otherwise). The distance between the pulsar
and the star is ![]() . So
. So
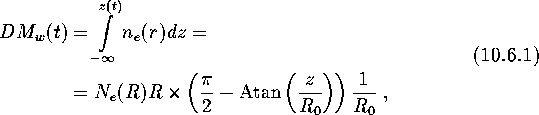
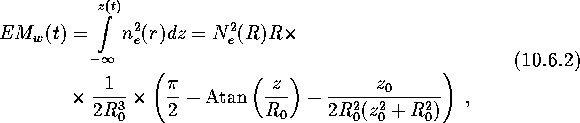
![]()
For the phases when the pulsar is behind the disk ( ![]() ) we also must consider dispersion and absorption due to the disk:
) we also must consider dispersion and absorption due to the disk:
![]()
![]()
Figure 31 gives an example of the calculated DM profile and light curve at frequencies of 660 and 1520 MHz. In these computations, the spectrum was approximated by a power law with exponent S=-0.5. It was also assumed that matter is locally homogeneous (not clumped) both in the stellar wind and in the disk.
Figure 31: The theoretical DM profile and light
curves at frequencies of 660 and 1520 MHz for PSRB1259-63 (Lipunov et
al., 1994a).
Note that the dispersion increases rapidly near the eclipse but, as it has actually been measured far from this phase, this influence is insignificant in comparison with the observational results.
How would refraction affect the propagation of radioemission in such a binary system? When passing through the dense layers of a stellar wind, the path of a radiowave is curved in such a way that the profile of the DM and the light curve may change considerably. One must use more general formulae in this situation (Lipunov and Prokhorov, 1987)[115]. Whether the approximation of straight propagation is valid or not can be concluded from the relation between the radiation frequency and plasma frequency at the point (on the line of sight) closest to the optical star. If z>0 this point is nearest, and if z<0 it coincides with the pulsar's location.
Recent observations of PSR B1259-63 (Melatos et al., 1995)[140] confirmed all the effects mentioned and seem to have revealed a disk-like wind outflow from the Be-star.