5.2 Система UBV и двухцветные (двухиндексные) диаграммы

Система UBV получила широкое распространение в первую очередь благодаря обилию стандартов по всему небу. В начале 90-х годов Мермийо составил общую сводку измерений в системе UBV, содержащую измерения более чем для звезд. Говоря о системе UBV в этом параграфе, мы остановимся на одном виде представления фотометрической информации, о котором не говорили ранее. Это двухцветные, или двухиндексные, диаграммы.

Если в системе более двух полос, то можно составить несколько показателей цвета и представить на диаграмме зависимость одного показателя от другого. Такие диаграммы имеют очень большое значение как для определения некоторых физических параметров, так и для решения вопросов, связанных с различными редукциями фотометрических наблюдений.

Рис. 5.1: Двухцветная диаграмма (U-B,B-V) для типичных звезд разных спектральных типов. Данные из каталога З.Свидерскене

На рис.5.1 показана двухцветная диаграмма , построенная для нормальных (непокрасненных) распределений энергии в спектрах звезд различных типов (по данным З.Свидерскене).

Если бы мы, нанося на двухцветную диаграмму наблюдательные данные, сразу умели отбирать только точки, соответствующие звездам одного определенного класса светимости, то для не слишком далеких от Солнца звезд, не испытавших существенного поглощения межзвездным веществом, мы могли бы сразу производить спектральную классификацию. На линии нормальных показателей цвета (часто ее на жаргоне фотометристов называют линией нормальных цветов, но мы уже договорились о терминологии), т.е. на последовательности непокрасненных звезд одного класса светимости, каждый спектральный подкласс занимает довольно определенное место. Для звезд нормального химического состава такая классификация может производиться с погрешностью 2-3 спектральных подкласса. Произведя классификацию, всегда можно сопоставить такой звезде кривую распределения энергии (например, из каталогов Страйжиса и Свидерскене), и таким образом задача восстановления распределения энергии будет решена.

Но на эту принципиальную возможность решения задачи накладывается масса осложнений.

Во-первых, линии нормальных показателей цвета для разных классов светимости на плоскости двухцветной диаграммы в некоторых точках пересекаются или идут близко друг к другу.

Во-вторых, существует такое неприятное для спектральной классификации явление, как межзвездное поглощение света, под влиянием которого звезда со своего места на линии нормальных показателей цвета смещается по обеим координатам в сторону увеличения показателей цвета. Линии, по которым происходит это смещение, часто называют линиями покраснения, или линиями нарастающего поглощения. В случае монохроматических величин они являются прямыми, но для гетерохромных полос несколько искривляются, а угол наклона линий покраснения становится функцией величины поглощения. Причина этого искривления в та же, что и у эффекта Форбса. Более красные лучи пределах гетерохромной полосы ослабляются меньше, чем более голубые.

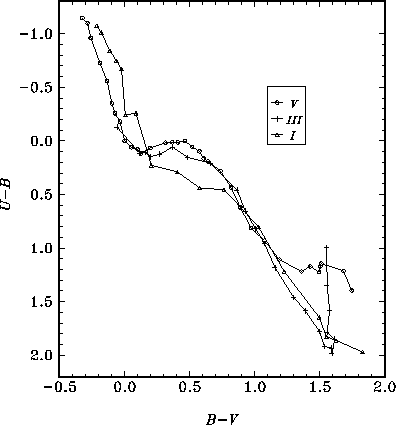
Реальная двухцветная диаграмма гораздо сложнее, чем идеализированный вариант на рис.5.1.

Рис. 5.2: Двухцветная диаграмма (U-B,B-V) для объектов каталога BS

Если звезда по линии покраснения сместилась с последовательности нормальных показателей цвета из точки с координатами в точку с координатами (U-B,B-V), то величины

(5.3)

(5.4)

Перепишем равенство 5.3 в виде

(5.5)

(5.6)

(5.7)

Методы спектральной классификации, основанные на использовании величины , принято называть -методами. Ими пользуются как в случае квазимонохроматических, так и в случае гетерохромных фотометрических полос. Для монохроматических полос отношение избытков цвета есть величина постоянная. В случае гетерохромных полос обязательно нужно помнить, что величина отношения избытков зависит от спектрального класса и вида закона межзвездного поглощения. Для хорошо разработанных фотометрических систем задача определения этих зависимостей должна быть решена наблюдательным или теоретическим путем. Разумеется, в любом случае зависимость от межзвездного поглощения -- это уже величина второго порядка малости. Если у нас имеются величины , даже вычисленные с не совсем правильным значением отношения избытков цвета, то эти величины в значительной степени свободны от влияния межзвездного поглощения и ими, наряду с двухцветными диаграммами, можно пользоваться для целей спектральной классификации, сравнивая наблюдательные данные с графиками . (См. упомянутую во введении монографию Страйжиса, стр.104, рис. 27). Для четырехполосного варианта этой системы интерес представляют зависимости или .

Итак, из рассмотрения графиков , и можно с некоторой степенью точности и надежности определить спектральный тип звезды, а следовательно, и вид распределения энергии в ее спектре. Еще раз подчеркнем, что с абсолютно строгих позиций, не зная ни спектрального типа, ни межзвездного покраснения, т.е. не имея представления (хотя бы грубого!) о распределении энергии во внеатмосферном спектре звезды, мы не можем правильно определить поправку выноса за атмосферу, и перевести звездные величины из одной фотометрической системы в другую.

Несколько позднее введения трех полос UBV Джонсон добавил в свою систему другие полосы в красной и инфракрасной областях. В частности, появилась полоса . Как уже отмечалось, она реализовывалась с помощью кислородно-цезиевого катода (S1), причем получила очень большую ширину: начинается от , имеет максимум около  и простирается до   (см.рис.1.1). Для таких широких полос задача выноса за атмосферу и редукций в другие системы решается плохо. Чем уже полоса пропускания, тем меньше влияет на все вычисления неточное знание действительного распределения энергии в спектре и атмосферных параметров. Для очень широких спектральных полос с полушириной в несколько тысяч ангстрем при всем старании невозможно для произвольно взятого случая достаточно хорошо провести редукции как за атмосферу, так и из одной фотометрической системы в другую.