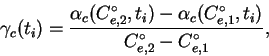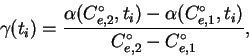В классическом ![]() -методе не предусмотрены специальные меры
на случай работы в условиях ночи с переменной экстинкцией.
Поэтому и в методе контрольных звезд Никонова, и в оригинальной
статье, излагающей метод Сарычева, есть обобщение на случай
линейной зависимости коэффициента экстинкции от показателя
цвета. Естественно, что при этом вычислительная процедура сильно
усложняется. Рассмотрим такое обобщение на примере метода
контрольных звезд.
-методе не предусмотрены специальные меры
на случай работы в условиях ночи с переменной экстинкцией.
Поэтому и в методе контрольных звезд Никонова, и в оригинальной
статье, излагающей метод Сарычева, есть обобщение на случай
линейной зависимости коэффициента экстинкции от показателя
цвета. Естественно, что при этом вычислительная процедура сильно
усложняется. Рассмотрим такое обобщение на примере метода
контрольных звезд.
Пусть имеются линейные соотношения между коэффициентами
экстинкции
![]() и
и
![]() и разностью
внеатмосферных показателей цвета
и разностью
внеатмосферных показателей цвета ![]() и
и ![]() программной и
экстинкционной звезд соответственно:
программной и
экстинкционной звезд соответственно:
Влияние эффекта Форбса можно приблизительно представить в
следующем виде:
Если поправки
![]() и
и
![]() придать наблюдаемым значениям
звездной величины и показателя цвета соответственно, то уравнения (6.27)
и (6.28) примут вид
придать наблюдаемым значениям
звездной величины и показателя цвета соответственно, то уравнения (6.27)
и (6.28) примут вид
Никонов указывает, что для определения звездной величины и
цвета экстинкционной звезды в методе контрольных звезд можно
полностью использовать монохроматическую методику, если
подобрать контрольные звезды с показателями цвета ![]() настолько близкими к показателям цвета экстинкционной звезды
настолько близкими к показателям цвета экстинкционной звезды
![]() , чтобы можно было пренебречь поправками
, чтобы можно было пренебречь поправками
![]() и
и
![]() .
Такие контрольные звезды Никонов называет контрольными звездами первого
рода.
.
Такие контрольные звезды Никонов называет контрольными звездами первого
рода.
Для определения коэффициентов ![]() и
и ![]() применяются
контрольные звезды второго рода, т.е. сильно отличающиеся по
показателю цвета.
применяются
контрольные звезды второго рода, т.е. сильно отличающиеся по
показателю цвета.
Для определения ![]() сначала выносим за атмосферу
наблюденные показатели цвета контрольных звезд второго
рода
сначала выносим за атмосферу
наблюденные показатели цвета контрольных звезд второго
рода ![]() , используя для определения коэффициента экстинкции
истинное значение показателя цвета экстинкционной звезды
, используя для определения коэффициента экстинкции
истинное значение показателя цвета экстинкционной звезды ![]() ,
определенное по контрольным звездам первого рода. Таким образом находим
приближенное значение
,
определенное по контрольным звездам первого рода. Таким образом находим
приближенное значение
Для определения ![]() необходимо решить аналогичную систему
условных уравнений:
необходимо решить аналогичную систему
условных уравнений:
Если все же будет признано, что необходимо получать мгновенные значения
коэффициентов ![]() и
и ![]() , то это потребует наблюдений второй
экстинкционной звезды, с показателем цвета, резко отличающимся от
основной. Наблюдения двух экстинкционных звезд ``1'' и ``2'' с показателями
цвета
, то это потребует наблюдений второй
экстинкционной звезды, с показателем цвета, резко отличающимся от
основной. Наблюдения двух экстинкционных звезд ``1'' и ``2'' с показателями
цвета
![]() и
и
![]() и позволяют строить
графики ночного хода экстинкции
и позволяют строить
графики ночного хода экстинкции