<< 6.7 Метод Сарычева | Оглавление | 6.9 gamma-модификация метода контрольных ... >>

6.8 Классический gamma-метод

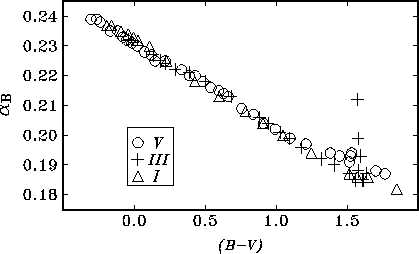
Рассмотренные выше методы являются методами, применимыми для монохроматического излучения. В случае гетерохромных фотометрических полос существует зависимость бугеровских коэффициентов экстинкции от распределения энергии в спектре звезды и, как следствие, от ее показателей цвета. На рис.6.2 показана вычисленная по формуле (1.8) зависимость коэффициента атмосферной экстинкции $\alpha(B)$ в полосе $B$ системы UBV от показателя цвета (B-V) звезд различных спектральных классов при прохождении света от них через одну атмосферную массу для высокогорной обсерватории. Видно, что для этого случая в широком интервале спектральных классов зависимость можно считать линейной; характерный разброс точек около нее составляет несколько тысячных долей звездной величины.

Рис. 6.2: Зависимость коэффициента атмосферной экстинкции $\alpha _B$ в полосе $B$ системы UBV от показателя цвета (B-V) для звезд различных спектральных типов
\begin{figure}\begin{center} \epsfxsize =0.8\textwidth\epsfbox{lfig6_2.eps}\end{center}\vspace{14pt} \end{figure}

Пусть мы пронаблюдали в данной гетерохромной полосе две стандартных звезды с номерами 1 и 2 и внеатмосферными показателями цвета $C^\circ_1$ и $C^\circ_2$ при разных воздушных массах $M(z_1)$ и $M(z_2)$ и получили измеренные звездные величины $m_1(z_1)$ и $m_2(z_2)$. Этим измерениям будут соответствовать различные коэффициенты атмосферной экстинкции $\alpha(C^\circ_1)$ и $\alpha(C^\circ_2)$. Внеатмосферные величины обеих звезд для этого случая будут равны

\begin{displaymath} m^\circ_1=m_1(z_1)-\alpha(C^\circ_1)\,M(z_1), \end{displaymath} (6.42)


\begin{displaymath} m^\circ_2=m_2(z_2)-\alpha(C^\circ_2)\,M(z_2), \end{displaymath} (6.43)

Из предположения о линейности зависимости $\alpha$ от $C$ следует
\begin{displaymath} \alpha(C^\circ_2)=\alpha(C^\circ_1 )+\gamma\,(C^\circ_2-C^\circ_1), \end{displaymath} (6.44)

т.е. экстинкционный коэффициент для второй звезды равен экстинкционному коэффициенту для первой звезды плюс поправка, пропорциональная разности показателей цвета этих звезд. Поскольку исторически сложилось так, что в формуле (6.44) коэффициент пропорциональности принято обозначать буквой $\gamma $, то методы учета атмосферной экстинкции, основанные на предположении о линейной зависимости коэффициента экстинкции от показателя цвета, часто называют гамма-методами.

Вычтем (6.43) из (6.42) и подставим туда (6.44). Получим

\begin{displaymath} \Delta m^\circ_{1-2}= m_1(z_1)-m_2(z_2)-\alpha(C^\circ_1)\Delta M(z)+ \gamma\,\Delta C^\circ\,M(z_2). \end{displaymath} (6.45)

В этом уравнении величина $m_1(z_1)-m_2(z_2)$ получается из наблюдений, известны $\Delta M(z)$ и $M(z_2)$. Поскольку мы имеем дело со стандартами, известны $\Delta m^\circ_{1-2}$ и $\Delta C^\circ$. Неизвестными являются $\alpha$ и $\gamma $.

Пусть у нас имеются на разных воздушных массах два стандарта с одинаковыми показателями цвета. Для них $\Delta C^\circ = 0$. Следовательно, член с $\gamma $ равен нулю и можно определить $\alpha(C^\circ_1)$. Если же мы подберем два стандарта, отличающиеся по показателю цвета, и пронаблюдаем их на одинаковых зенитных расстояниях, то есть при $\Delta M(z)=0$, член с $\alpha$ будет равен нулю и можно будет определить $\gamma $.

На практике $\gamma $-метод не слишком удобен, так как приходится располагать набором стандартов различных спектральных классов, чтобы удовлетворить то требованию одинаковости, то сильному различию показателей цвета. Они должны быть расположены на небе так, чтобы их было легко наблюдать на одинаковых зенитных расстояниях. Впрочем, при применении $\gamma $-метода обычно полагают, что коэффициент $\gamma $ не зависит ни от интервала спектральных классов, ни от значения $\alpha$ (то есть одинаков для всех ночей). В этом случае $\gamma $ считается постоянной фотометрической системы и определяют эту величину редко: один-два раза в год.

$\gamma $-метод, практически в его классической интерпретации, широко применялся и применяется в различных обсерваториях. Его использование вполне оправдано для фотометрических полос, расположенных в ``спокойных'' областях функции распределения энергии в спектре.


<< 6.7 Метод Сарычева | Оглавление | 6.9 gamma-модификация метода контрольных ... >>