<< 6.9 Гамма-модификация метода ... | Оглавление | 6.11 Mетодика Тянь-Шаньской обс... >>

6.10 Метод Зданавичюса для показателей цвета

Как мы убедились, гетерохромный вариант метода контрольных звезд Никонова, громоздок и не свободен от упрощений, в применимости которых еще нужно убеждаться. И это только для простейшего случая линейной зависимости коэффициентов экстинкции от показателей цвета. В общем же случае такой зависимости нет!

Рис. 6.3: Зависимость коэффициента атмосферной экстинкции $\alpha _U$ в полосе $U$ системы UBV от показателя цвета (B-V) для звезд различных спектральных типов
\begin{figure}\begin{center} \epsfxsize =0.8\textwidth\epsfbox{lfig6_3.eps}\end{center}\end{figure}

Это убедительно показывает график на рис.6.3. Как и на рис. 6.2, это не непосредственные данные наблюдений, а результат вычислений основного интеграла. Видно, что для всех классов светимости нет не только линейности, но и монотонности хода кривой. Зависимости различны для разных классов светимости. При показателе цвета $B-V=0.5$ применение для звезд-сверхгигантов коэффициента экстинкции, полученного по звездам-карликам, приведет к ошибке около 5на каждую единицу атмосферной массы. Отметим, что качественно вид этого графика такой же, как и двухцветной диаграммы $(U-B),(B-V)$. Причиной немонотонности является возникновение и, затем, исчезновение бальмеровского скачка по мере изменения поверхностной температуры звезд со спектральным классом. Никакие линейные упрощения здесь уже не помогут. Нужно применять принципиально другие методы. По-видимому первым, кто создал и применил последовательно-гетерохромный метод учета атмосферной экстинкции, был К.Зданавичюс. Он разрабатывал метод выноса за атмосферу показателей цвета среднеполосной Вильнюсской системы, но с успехом применил его и для широкополосных систем.

В методе Зданавичюса для каждого конкретного набора кривых реакции делается специальный расчет. Рассмотрим этот метод на примере показателей цвета широкополосной системы $UBVR$.

При расчетах Зданавичюс подставлял в основную гетерохромную формулу (1.8) кривые реакции фотометрической системы $T_i(\lambda)$, некоторую кривую $p(\lambda)$, характеризующую поглощение в стандартной атмосфере и нормальные распределения энергии в спектрах звезд разных спектральных типов $E(\lambda )$, видоизменяя их в разной степени в соответствии с законом межзвездного покраснения. Функция $p(\lambda)$ представляет некоторую среднюю атмосферу, а не реальную атмосферу в момент наблюдений. Однако, поскольку метод разрабатывался только для выноса показателей цвета, Зданавичюс счел возможным пренебречь отклонениями реальной атмосферы от стандартной модели, считая, что вариации экстинкции неселективны.

Рассмотрим сначала самый сложный случай выноса показателя цвета $U-B$.

Пусть $C^{\circ}_{U-B}$ -- внеатмосферный показатель цвета звезды, а $C_{U-B}(z)$ -- измеренный показатель цвета под атмосферой при зенитном расстоянии $z$. Разность этих показателей, то есть величину выноса, Зданавичус представляет в виде

\begin{displaymath} C_{U-B}(z) - C^{\circ}_{U-B} = {\alpha}_{UB}'\,M(z) + r_{UB}[M(z)]^2. \end{displaymath} (6.60)

Здесь ${\alpha}_{UB}'$ -- неизвестный коэффициент экстинкции, а $r_{UB}$ -- коэффициент Форбса, который учитывает нелинейность зависимости коэффициента экстинкции от воздушной массы. Эффект Форбса явно существен для ультрафиолетовой полосы, так как тут самый крутой наклон зависимости коэффициентов экстинкции от длины волны, из-за крутизны релеевской функции и функции поглощения озоном. Коэффициент $r_{UB}$, в свою очередь, зависит от спектрального класса, межзвездного поглощения и от закона атмосферной экстинкции. Зданавичюс пришел к выводу, что все эти зависимости приближенно учитываются формулой
\begin{displaymath} r_{UB} = -0.028{\alpha}_{UB}' , \end{displaymath} (6.61)

следовательно,
\begin{displaymath} {\alpha}_{UB}' = \frac{C_{U-B}(z) - C^{\circ}_{U-B}} {M(z)\,[1-0.028\,M(z)]} . \end{displaymath} (6.62)

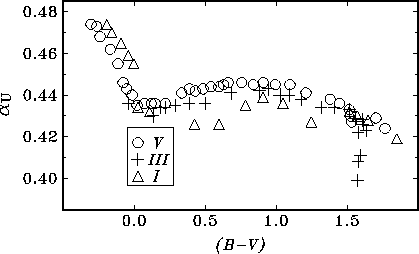
Расчеты по интегральной формуле, с помощью которых можно построить графики типа показанного на рис.6.3, позволяют определить наклон линий нарастающего поглощения. Зданавичюс строил графики $\alpha_{UB}$,(U-B) и $\alpha_{UB}$,(B-V). На обоих графиках угловой коэффициент этих линий оказался одинаковым и равным $-0.012$.

После этого были сформированы независимые от межзвездного поглощения коэффициенты

\begin{displaymath} {\varkappa}_{UB}' = {\alpha}_{UB}' + 0.012(U-B) \end{displaymath} (6.63)

и
\begin{displaymath} {{\varkappa}_{UB}^{BV}}' = {{\alpha}_{UB}}' + 0.012(B-V) \end{displaymath} (6.64)

Зданавичюс обнаружил, что при всей сложности вида зависимостей коэффициентов $\varkappa_{UB}$ от (U-B),(B-V) и $Q_{UBV}$, эти коэффициенты удовлетворительно выражается комбинацией двух параметров $Q$:

\begin{displaymath} {\varkappa}_{UB} = 0.37 - 0.067\,Q_{UBV} + 0.073\,Q_{BVR}, \end{displaymath} (6.65)

и
\begin{displaymath} {{\varkappa}_{UB}^{BV}}' = 0.36 - 0.078\,Q_{UBV} + 0.069\,Q_{BVR}, \end{displaymath} (6.66)

Вычисленные по формулам (6.65) и (6.66) коэффициенты экстинкции отличаются от действительных не более чем на 0.02. В этих формулах неявно заключена зависимость $\alpha_{UB}$ от спектрального класса и класса светимости, выраженная через параметры $Q$. Подчеркнем важность полосы $R$. Без параметра $Q_{BVR}$ не удалось бы аппроксимировать коэффициенты никакой линейной формулой. Для показателя цвета $B-V$ дело обстоит много проще, так как изменение $\varkappa_{BV}$ от спектрального класса звезды хорошо учитывается формулой


\begin{displaymath} \varkappa_{BV} = 0.18 - 0.05\,Q_{BVR}. \end{displaymath} (6.67)

Для показателя цвета $V-R$ Зданавичюс применяет классический $\gamma $-метод. Значение $\gamma=0.0105$ и
\begin{displaymath} \alpha_{VR} = \alpha_{VR}(A0V) + 0.0105\,(V-R) . \end{displaymath} (6.68)

Для какой-либо другой фотометрической системы, например для полос WBVR, можно таким же приемом получить свои коэффициенты. Например, формула, аналогичная соотношению (6.66) такова:
(6.69)

Заметим, что значения числовых коэффициентов при $Q$ в формуле (6.69) примерно в 2-3 раза менее таковых в формуле (6.66). Следовательно, в системе WBVR ошибки определения параметров $Q$ будут слабее влиять на ошибки выноса, чем в системе $UBVR$.


<< 6.9 Гамма-модификация метода ... | Оглавление | 6.11 Mетодика Тянь-Шаньской обс... >>