5. Критический радиус частицы хвоста кометы: вычисление и анализ

Разделы

• 5.1. Вычисление критического радиуса частицы хвоста кометы
• 5.2. Критический радиус частицы хвоста кометы: численные результаты и анализ

В данном параграфе будет представлено аналитическое выражение для критического радиуса частицы хвоста кометы с учетом сил тяготения, действующих со стороны Солнца и ядра кометы, а также силы светового давления (первый пункт параграфа), будет дан анализ полученного результата на примерах однопараметрических зависимостей от других физических параметров модели (второй пункт параграфа) для кометы Галлея.

5.1. Вычисление критического радиуса частицы хвоста кометы

Итак, в данном пункте автор представит аналитический результат для критического радиуса частицы хвоста кометы. Воспользуемся результатами предыдущего параграфа. Рассмотрим третье уравнение системы (35).

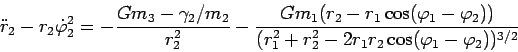(36)

			(37)
			(38)
			(39)

здесь - радиальное ускорение частицы.

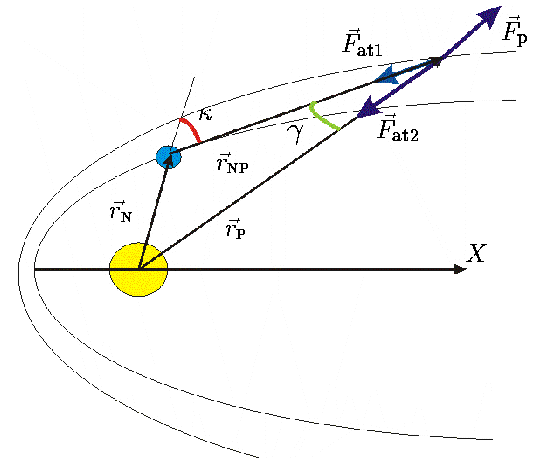
Рис. 6. Частица хвоста кометы, находящаяся под действием сил тяготения Солнца, ядра кометы и силы светового давления.

Учтем, что массу сферической частицы можно представить в виде , где - массовая плотность вещества частицы, а также, согласно рис. 6, нетрудно видеть, что

(40)

(41)

(42)

Из (41), (42) очевидно, что критический радиус частицы зависит не только от значений фундаментальных констант, но также от положения частицы в пространстве (расстояния , , и угол ), от характеристик кометы (, , - показатель преломления вещества, из которого состоит частица) и, конечно, характеристик Солнца (, ).

Представим полученный результат в несколько иной форме, а именно как функцию , и - угла отклонения частицы кометы от радиального направления на ядро. Согласно теореме косинусов из треугольника (смотри рис. 6) следует, что:

(43)

			(44)

(45)

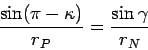
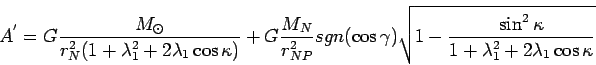(46)

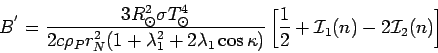(47)

Из выражения (45) следует выражение для критического радиуса частицы

(48)

5.2. Критический радиус частицы хвоста кометы: численные результаты и анализ

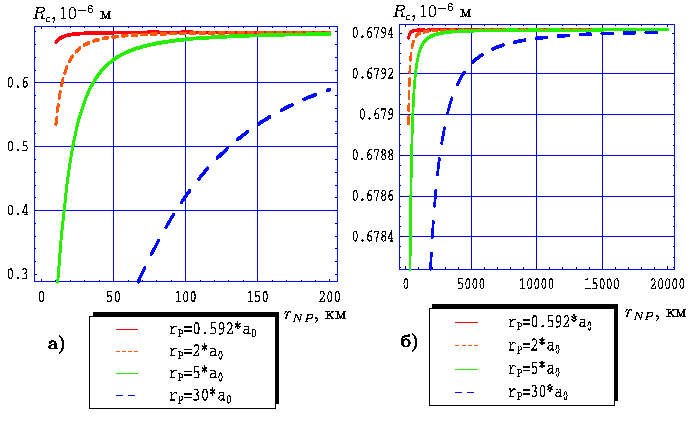
Рис. 7. Зависимость критического радиуса частицы от расстояния до ядра кометы при фиксированных значениях ρP=820 кг/м3, MN=6.1014 кг, n=1.29, γ=1o (здесь a0 - астрономическая единица).

В данном пункте рассмотрим зависимость критического радиуса частицы хвоста кометы от параметров данной физической системы (, , , ) на примере кометы Галлея, предполагая, что частица состоит из водного льда, находящегося при низкой температуре ⁷.

Рис. 8. Зависимость критического радиуса частицы от расстояния до Солнца при фиксированных значениях ρP=820 кг/м3, MN=6.1014 кг, n=1.29, γ=1o.

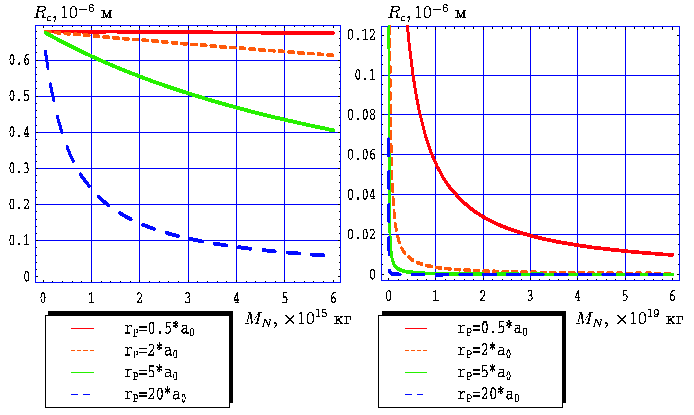
Рис. 9. Зависимость критического радиуса частицы от массы ядра кометы при фиксированных значениях ρP=820 кг/м3, MN=6.1014 кг, n=1.29, γ=1o.	Рис. 10. Зависимость критического радиуса частицы от массы ядра кометы при фиксированных значениях ρP=820 кг/м3, MN=6.1014 кг, n=1.29, γ=1o.

Рис. 11. Зависимость критического радиуса от плотности вещества частицы хвоста кометы при фиксированных значениях ρP=820 кг/м3, MN=6.1014 кг, n=1.29, γ=1o.	Рис. 12. Зависимость критического радиуса от плотности вещества частицы хвоста кометы при фиксированных значениях показателя преломления ρP=820 кг/м3, MN=6.1014 кг, n=1.29, γ=1o.

На рисунках 7 представлены зависимости критического радиуса частицы от расстояния до ядра кометы при фиксированных значениях расстояния от Солнца до частицы . Очевидно, что радиус фактически не зависит от параметра , когда комета находится в перигелии, а с увеличением критический радиус становится все более "чувствительным" к расстоянию . Действительно, находясь в перигелии орбиты, доминирующее влияние на частицу оказывает именно Солнце. По мере удаления частицы от Солнца его воздействие уменьшается и все более существенным становится гравитационное действие ядра кометы. На расстояниях в десятки астрономических единиц действие ядра кометы является определяющим.

На рисунках 8 представлены зависимости критического радиуса частицы от расстояния до Солнца при фиксированных значениях расстояния . Из рисунка 8.а, очевидно, что критический радиус частицы "чувствителен" к параметру , когда частица находится вблизи поверхности ядра км (значение изменяется в пределах от м до м при вариации в пределах ). На расстояниях км гравитационное влияние ядра кометы становится несущественным, и поэтому критический радиус остается постоянным. Заметим также, что критический радиус "чувствителен" к параметру при расстоянии км и при вариации в пределах (значение параметра изменяется в пределах от м до м, смотри рис. 8.б). Все кривые указанных рисунков свидетельствуют об уменьшении гравитационного влияния Солнца при увеличении расстояния .

На рисунках 9-10 представлены зависимости критического радиуса частицы от массы ядра кометы при фиксированных значениях расстояния . Очевидно, что с увеличением массы ядра кометы критический радиус падает, поскольку гравитационное влияние ядра кометы становится все более существенным (сила тяготения пропорциональна ). Заметим также, что на больших расстояниях критический радиус "чувствителен" к массе ядра кометы (в случае "легких" ядер, т.е. кг). В случае "тяжелых" ядер критический радиус "чувствителен" к массе уже на существенно меньших расстояниях ( при ).

На рисунках 11-12 представлены зависимости критического радиуса частицы от плотности вещества частицы хвоста кометы при фиксированных значениях расстояния . Очевидно, что с увеличением плотности критический радиус падает, это вновь следствие увеличения гравитационных сил, (сила притяжения растет пропорционально ). При этом зависимость критического радиуса от плотности является существенной на любых расстояниях, поскольку данный параметр определяет величину сил тяготения. Заметим также, что критический радиус частицы фактически не зависит от показателя преломления вещества частицы, поскольку интегралы , , содержащие зависимость от параметра , дают очень малый вклад в определение силы светового давления (смотри рис. 12).