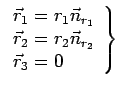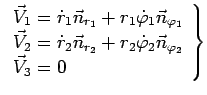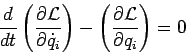В данном параграфе автор представит математические основы подхода к поиску решения поставленных задач. В качестве такого подхода автор предпочитает использовать Лагранжев подход.

Для получения уравнений движения тел рассматриваемой модели необходимо прежде всего явно задать функцию Лагранжа - скалярную аналитическую функцию параметров модели. Поэтому первым этапом в применении подхода Лагранжа будет построение функции Лагранжа.

4.1. Построение функции Лагранжа

Наиболее общая структура функции Лагранжа может быть представлена в виде [4].

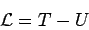(21)

здесь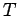

- суммарная кинетическая энергия тел рассматриваемой системы.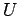

- их потенциальная энергия взаимодействия.

Модель физической системы составляют три тела, следовательно, 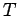может быть представлена в виде ⁶:

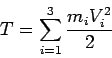(22)

Потенциальная энергия взаимодействия представляется двумя типами слагаемых:

слагаемыми, отвечающими за гравитационное взаимодействие

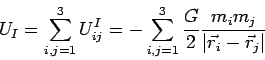(23)

слагаемыми, определяемыми действием излучения (смотри выражение (20))

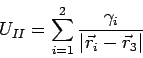(24)

где

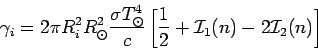(25)

В итоге функция Лагранжа принимает вид:

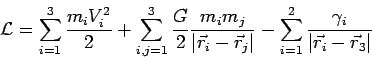(26)

4.2. Уравнения движения тел рассматриваемой модели

Вторым этапом в применении подхода Лагранжа является определение уравнений движения ядра и частицы кометы на основе явно заданной функции Лагранжа. Но прежде чем приступить к поиску данных уравнений, необходимо определить ряд дополнительных физических условий, при которых мы и будем искать решения поставленных задач. Будем полагать, что

в начальный момент времени вектора начальных скоростей и ускорений лежат в одной плоскости. Следовательно, движение тел модели будет осуществляться в этой плоскости в любой последующий момент времени.
По-прежнему выполняется условие (1), т.е.

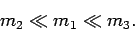(27)
В силу условия (27) частица существенно не влияет на характер движения ядра и Солнца, поэтому при определении уравнений движения последних мы будем пренебрегать слагаемыми, отвечающими за гравитационное действие частицы.
В силу неравенства (27) Солнце можно рассматривать как неподвижный силовой центр, в гравитационном поле которого, движутся другие тела системы. Задача о поиске законов движения тел рассматриваемой модели с указанными выше физическими условиями была названа Пуанкаре плоской ограниченной задачей трех тел [5].
Поскольку ядро кометы является макроскопическим телом (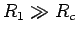), то действие светового давления на ядро кометы много меньше гравитационного притяжения Солнцем. Следовательно, при определении уравнения движения ядра кометы автор будет пренебрегать слагаемыми, отвечающими за указанное действие.

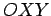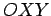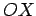Согласно выше сказанному выберем инерциальную систему отсчета и свяжем ее с геометрическим центром Солнца. Введем плоскую систему координат (плоскость совпадает с плоскостью орбиты ядра кометы), при этом начало координат совпадает с геометрическим центром Солнца, ось направим на афелий кометы. Тогда радиусы-векторы и скорости тел системы представляются в виде:

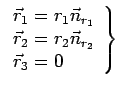(28)

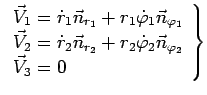(29)

Тогда функция Лагранжа (26) принимает следующий вид:


			(30)

Наиболее общая структура уравнений Лагранжа второго рода представляется в виде:

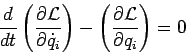(31)

здесь

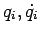- обобщенные координаты и скорости системы. В качестве обобщенных координат принимаем полярные координаты ядра и частицы кометы. Следовательно, уравнения движения принимают вид:

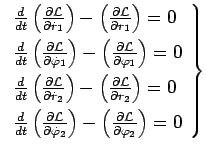(32)

с учетом (30) систему уравнений (32) можно представить в виде:

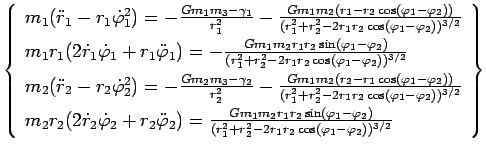(33)

или

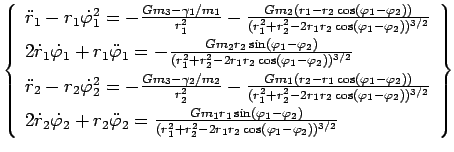(34)

последняя система уравнений может быть редуцирована с учетом физических условий, рассмотренных в начале данного пункта, к следующему виду.

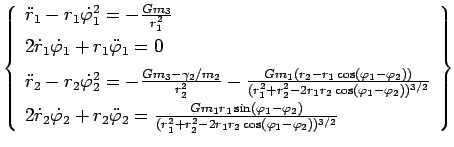(35)

Система уравнений (35) есть система уравнений движения ядра и частицы кометы под действием сил тяготения и силы светового давления, решение которой определяет законы движения указанных тел и, следовательно, результаты плоской ограниченной задачи трех тел.

<< 3. Сила светового давления ... | Оглавление | 5. Критический радиус частицы >>

4. Лагранжев подход в описании движения тел рассматриваемой модели

Разделы

4.1. Построение функции Лагранжа

4.2. Уравнения движения тел рассматриваемой модели