| (2.1) |
Основным объектом исследования в настоящей главе является звездный диск, представляющий, как правило, наиболее яркую и впечатляющую своими структурными особенностями подсистему спиральных галактик. В § 2.1 мы построим довольно простую самосогласованную модель неоднородного дифференциально вращающегося горячего звездного диска конечной толщины. Затем в § 2.2 выведем уравнение, описывающее в рамках построенной модели дисперсионные свойства неосесимметричных возмущений малой амплитуды в плоскости звездного диска и изучим ветви его колебаний. Влияние различных факторов на устойчивость гравитирующих дисков рассмотрим на качественном уровне в § 2.3. В следующем параграфе мы определим условия устойчивости звездного диска, учитывающие худшую стабилизируемость неосесимметричных возмущений по сравнению с осесимметричными. И наконец, последний § 2.5 посвящен исследованию устойчивости звездного диска относительно изгибных возмущений и формулированию соответствующих условий устойчивости. Во всей этой главе мы будем последовательно проводить сравнение полученных результатов и предсказаний теории с данными наблюдений, краткий обзор которых приведен в главе 1. Отметим также, что вопросы происхождения спирального узора галактик в этой главе практически не затрагиваются, поскольку им посвящена глава 6. Основные результаты, полученные методом численного эксперимента, будут обсуждаться в главе 3.
Характерное время, в течение которого параметры движения отдельной
звезды могут заметно измениться благодаря парному гравитационному
взаимодействию с другими звездами в дисках плоских галактик,
намного больше времени существования этих систем
[215]. Поэтому структуру и динамику
звездных дисков галактик с хорошей точностью можно описывать с
помощью бесстолкновительного кинетического уравнения. В декартовых
координатах это уравнение имеет вид
Звездные диски галактик в значительной мере обладают осевой
симметрией, что является естественным следствием их вращения. По
этой причине для решения многих проблем динамики звездного диска
удобно пользоваться уравнением (2.1), записанным
в цилиндрических координатах ![]() [163]:
[163]:
В осесимметричных задачах или системах без
газа 2.2
гравитационный потенциал, определяющий динамику звездного диска,
практически можно считать самосогласованным, и тем самым связать
величины ![]() и
и ![]() через объемную плотность звездного диска
через объемную плотность звездного диска
![]() уравнением Пуассона
уравнением Пуассона
Выше уже упоминалась относительная малость амплитуд неосесимметричных
возмущений плотности звездного диска. Кроме того, если отвлечься от
упомянутых особенностей, распределения различных величин в дисках
практически не изменяются в течение временных промежутков порядка
нескольких оборотов диска. И тем самым функцию распределения звезд диска
можно представить в виде суммы стационарной осесимметричной
![]() и ``возмущенной''
и ``возмущенной''
![]() компонент.
компонент.
Как уже отмечалось в обзоре наблюдательных данных (см.
§ 1.1), основным движением звезд в
диске является их вращение вокруг оси симметрии плоской галактики.
В соответствии с этим удобно выделить угловую скорость вращения
диска
Равновесная (стационарная и осесимметричная) компонента функции
распределения звезд диска, согласно (2.7), должна
удовлетворять уравнению
Из этих данных в первую очередь следует, что характерная
полутолщина звездного диска ![]() много меньше его радиуса
много меньше его радиуса
![]() . Это означает, что в уравнении (2.9)
. Это означает, что в уравнении (2.9)
![]() и в простейшем приближении
однородного по толщине диска из (2.9) вытекает
оценка частоты колебаний звезд поперек плоскости диска [см.
(1.4)]:
и в простейшем приближении
однородного по толщине диска из (2.9) вытекает
оценка частоты колебаний звезд поперек плоскости диска [см.
(1.4)]:
Приближение, определяемое неравенством (2.13),
дает основание заключить, что равновесие диска в радиальном
направлении обусловлено балансом центробежной и равновесной
гравитационной сил
Из приведенной выше оценки
![]() следует, что зависящая от
следует, что зависящая от ![]() часть
часть ![]() равновесного
гравитационного потенциала
равновесного
гравитационного потенциала
![]() .
Именно эта величина и определяет порядок по параметру
.
Именно эта величина и определяет порядок по параметру
![]() зависящей от
зависящей от ![]() -координаты компоненты угловой
скорости вращения диска. Действительно, так как полная
-координаты компоненты угловой
скорости вращения диска. Действительно, так как полная
![]() , где
, где
![]() , из условия равновесия диска
(2.14) получим
, из условия равновесия диска
(2.14) получим
Подставим разложения (2.18) в исходную систему
уравнений (2.8), (2.9). Тогда в
двух главных порядках по параметру ![]() получим:
получим:
Перейдем теперь к переменным ![]() ,
,![]() ,
, ![]() , связанным
с величинами
, связанным
с величинами ![]() ,
, ![]() ,
, ![]() соотношениями:
соотношениями:
Конкретный вид этой функции должен быть определен на основании
дополнительных данных. Непосредственно построить функцию
распределения ![]() , исходя из наблюдений, в настоящее время
представляется возможным только в солнечной окрестности Галактики.
Неравенство дисперсий скоростей звезд Галактики в трех взаимно
перпендикулярных направлениях является непреложным наблюдательным
фактом (см. п. 1.1.4).
Имеется ряд аналитических аппроксимаций наблюдаемых распределений
скоростей звезд, которые согласуются с наблюдениями только в
ограниченных интервалах скоростей (обзор литературы дан Шацовой
[223]). Наиболее известно распределение
Шварцшильда, которое представляет собой анизотропное
максвелловское:
, исходя из наблюдений, в настоящее время
представляется возможным только в солнечной окрестности Галактики.
Неравенство дисперсий скоростей звезд Галактики в трех взаимно
перпендикулярных направлениях является непреложным наблюдательным
фактом (см. п. 1.1.4).
Имеется ряд аналитических аппроксимаций наблюдаемых распределений
скоростей звезд, которые согласуются с наблюдениями только в
ограниченных интервалах скоростей (обзор литературы дан Шацовой
[223]). Наиболее известно распределение
Шварцшильда, которое представляет собой анизотропное
максвелловское:
Вычислим равновесное распределение объемной плотности в диске. Для
этого проинтегрируем (2.33) по пространству
скоростей
Суммируем полученные результаты. Равновесная функция распределения
звезд в главном порядке по малому параметру
![]() и в эпициклическом приближении,
определяемом неравенством (2.13), имеет вид
и в эпициклическом приближении,
определяемом неравенством (2.13), имеет вид
В этом разделе мы, следуя Вандервоорту [865], построили довольно простую модель звездного диска. Более сложные модели структуры диска поперек его плоскости можно найти, например, в упоминавшейся уже работе Вандервоорта и работе Бакола [266]. В последней, в частности, учтен вклад объемной плотности звезд сфероидальной подсистемы (см. также работу [140]). Мы их, однако, описывать не будем. Во-первых, потому, что довольно тонкие детали моделей весьма трудно сравнивать с данными наблюдений. Во-вторых, потому, что задача построения теории устойчивости этих моделей звездных дисков относительно как изгибных возмущений, так и возмущений в их плоскости пока не решена, и тем самым целостного понимания динамики звездного диска в рамках таких моделей не возникает.
В предыдущем разделе построена модель стационарного равновесного
звездного диска. Отклонения параметров диска (функции распределения,
потенциала и др.) от равновесных значений будем называть
возмущениями той или иной величины. Предположение о малой величине
амплитуд отклонений от равновесного состояния весьма привлекательно для
теоретического рассмотрения, поскольку исчезает одна из главных проблем
при решении кинетического уравнения -- его нелинейность. Изучение
возможных пространственных структур на фоне осесимметричного
стационарного состояния весьма популярно. В то же время для реальных
систем предположение о малой величине амплитуд возмущений часто
нарушается. Достижения в построении нелинейных моделей (речь не идет о
численных, см. гл. 3) невелики. Однако линейный подход позволяет весьма
успешно решать классическую задачу об устойчивости равновесной системы,
отвечая на вопрос о причинах роста со временем тех или иных
первоначально сколь угодно малых по амплитуде возмущений. В основе
анализа линейной устойчивости лежит дисперсионное уравнение,
определяющее временную динамику малых возмущений в зависимости от их
пространственной структуры. Из-за стационарности исходного диска
возмущения пропорциональны
![]() и будущее системы
определяется наличием и знаком мнимой части частоты
и будущее системы
определяется наличием и знаком мнимой части частоты ![]() (инкрементом). Рост со временем амплитуды в случае
(инкрементом). Рост со временем амплитуды в случае
![]() свидетельствует о неустойчивости системы.
свидетельствует о неустойчивости системы.
В данном параграфе мы получим дисперсионное уравнение, учитывающее неоднородность распределения равновесных параметров звездного диска.
Следуя Вандервоорту [866],
получим кинетическое уравнение, описывающее динамику возмущений
малой амплитуды в плоскости тонкого звездного диска. Для этого
представим полные функции распределения звезд и гравитационный
потенциал диска в виде суммы равновесных (![]() ) и
возмущенных (
) и
возмущенных (![]() ) величин:
) величин:
Для решения этой системы так же, как и в
п. 2.1.2, перейдем к переменным
действие-угол ![]() ,
, ![]() (2.24). Поскольку
(2.24). Поскольку ![]() , где
, где
![]() , то
, то
Уравнение (2.54) является линейным
дифференциальным уравнением в частных производных. Его
характеристики, определяющие невозмущенные траектории звезд в
плоскости диска, описываются уравнениями:
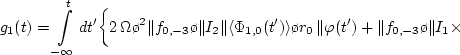 , а
другая, ориентированная в азимутальном направлении, равна
, а
другая, ориентированная в азимутальном направлении, равна
Для вычисления возмущенной функции распределения ![]() запишем
уравнение (2.54) в виде, удобном для применения в
дальнейшем метода интегрирования по траекториям
[112]:
запишем
уравнение (2.54) в виде, удобном для применения в
дальнейшем метода интегрирования по траекториям
[112]:
Коэффициенты уравнения (2.54) в связи со
стационарностью и осесимметричностью равновесного состояния диска
не зависят явно от времени и азимутальной координаты. Это
позволяет представить зависимость возмущенных величин ![]() ,
,
![]() от времени
от времени ![]() и угла
и угла ![]() в экспоненциальном виде
в экспоненциальном виде
![]() , где
, где
![]() -- частота возмущений,
-- частота возмущений, ![]() -- номер моды по
азимуту,
-- номер моды по
азимуту,
![]() -- азимутальное число. Такое
представление, в частности, означает, что предполагавшийся выше
при переходе от (2.54) к (2.57)
рост амплитуды возмущений во времени эквивалентен наличию у
частоты
-- азимутальное число. Такое
представление, в частности, означает, что предполагавшийся выше
при переходе от (2.54) к (2.57)
рост амплитуды возмущений во времени эквивалентен наличию у
частоты ![]() малой положительной мнимой части
-- инкремента.
малой положительной мнимой части
-- инкремента.
В радиальном направлении равновесный звездный диск неоднороден. Однако
мы можем ограничиться рассмотрением коротковолновых в этом направлении
возмущений
-- таких, характерный масштаб изменения которых мал по сравнению с
минимальным масштабом радиальной неоднородности диска. Роль
последнего в галактиках за пределами их центральных областей
обычно играет величина
![]() . Для изучения свойств таких
возмущений используют ВКБ-приближение, в котором радиальная
зависимость возмущенных величин полагается
. Для изучения свойств таких
возмущений используют ВКБ-приближение, в котором радиальная
зависимость возмущенных величин полагается
![]() , где
, где ![]() -- упоминавшийся выше характерный масштаб изменения возмущенных величин в
радиальном направлении (
-- упоминавшийся выше характерный масштаб изменения возмущенных величин в
радиальном направлении (![]() -- радиальное волновое число).
Таким образом, сформулированное выше условие применимости
ВКБ-приближения можно записать в виде 2.6
-- радиальное волновое число).
Таким образом, сформулированное выше условие применимости
ВКБ-приближения можно записать в виде 2.6
Для дальнейшего важно отметить, что мы не связываем решение рассматриваемой здесь задачи изучения динамики малых возмущений в звездном диске с исследованием поведения каких-либо глобальных структурных особенностей диска (например, спирального узора). Поэтому в отличие от подхода Лина и Шу [585, 586] не будем пренебрегать в (2.54) и (2.57) возмущенными азимутальными силами. Такой подход позволяет нам изучить дисперсионные свойства неосесимметричных возмущений в неоднородном звездном диске и получить условие его устойчивости относительно неосесимметричных возмущений в его плоскости [126, 128].
Вычислим фазу возмущений
![]() . Для этого перейдем в
двумерном пространстве волновых векторов (
. Для этого перейдем в
двумерном пространстве волновых векторов (![]() ,
, ![]() ) к
величинам
) к
величинам
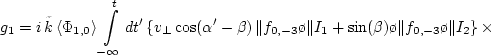 . Тогда с помощью уравнений
(2.56), описывающих невозмущенные траектории
звезд, нетрудно получить
. Тогда с помощью уравнений
(2.56), описывающих невозмущенные траектории
звезд, нетрудно получить
![\begin{displaymath}
g_1 = -\langle\Phi_{1,0}\rangle\sum\limits_{n=-\infty}^\inf...
...p[i\,\xi\sin(\alpha -
\beta) - i\,n\,(\alpha - \beta)]\times
\end{displaymath}](img903.gif)
Объемная плотность диска, создаваемая возмущенной функцией
распределения (2.52) с определяемой по
(2.66) величиной ![]() , может быть получена
интегрированием последней по пространству скоростей. В случае
равновесного диска [см. (2.42)] эта операция с
учетом разложения (2.65) приводит к следующему
выражению:
, может быть получена
интегрированием последней по пространству скоростей. В случае
равновесного диска [см. (2.42)] эта операция с
учетом разложения (2.65) приводит к следующему
выражению:
Поляченко и Фридман [163]
показали, что возмущения в плоскости диска, исследованию свойств
которых и посвящен этот раздел, в рамках линейной теории в модели
тонкого диска отщепляются от изгибных (мембранных) колебаний
диска. В последних локальная поверхностная плотность не
возмущается, а возмущения объемной плотности имеют ``дипольный''
вид. Поэтому при описании свойств возмущений в плоскости диска в
выражении (2.67) необходимо отбросить члены, не
дающие вклада в возмущенную поверхностную плотность:
Для вычисления возмущенной объемной плотности, обусловленной
вторым членом в (2.67), используем конкретный вид
равновесной функции распределения звезд ![]() (2.42). Кроме того, в соответствии с данными
наблюдений (см. § 1.1), показывающими,
что характерные толщины звездных дисков галактик слабо меняются
вдоль радиальной координаты, будем считать
(2.42). Кроме того, в соответствии с данными
наблюдений (см. § 1.1), показывающими,
что характерные толщины звездных дисков галактик слабо меняются
вдоль радиальной координаты, будем считать
![]() const.
В этом случае с учетом (2.40) имеем три
независимых параметра звездного диска, в качестве которых выберем
величины
const.
В этом случае с учетом (2.40) имеем три
независимых параметра звездного диска, в качестве которых выберем
величины ![]() ,
, ![]() ,
, ![]() . Тогда из
(2.33) следует:
. Тогда из
(2.33) следует:
Возмущения плотности диска ![]() приводят к возмущениям
гравитационного потенциала
приводят к возмущениям
гравитационного потенциала ![]() , и связь между этими
величинами определяется уравнением Пуассона [см.
(2.3)]:
, и связь между этими
величинами определяется уравнением Пуассона [см.
(2.3)]:
Уравнение (2.76) похоже на уравнение Шредингера,
описывающее движение частицы в потенциальной яме
![]() вдоль
вдоль ![]() - координаты
[89]. Однако для
(2.76) задача поставлена несколько по-иному: для
фиксированного значения ``энергии'' (
- координаты
[89]. Однако для
(2.76) задача поставлена несколько по-иному: для
фиксированного значения ``энергии'' (![]() ) необходимо найти
``глубину потенциальной ямы'' (
) необходимо найти
``глубину потенциальной ямы'' (
![]() ), в которой
может существовать заданный ``уровень энергии'' (
), в которой
может существовать заданный ``уровень энергии'' (![]() ). Нетрудно
видеть, что минимальная глубина такой ямы определяется безузловой
в
). Нетрудно
видеть, что минимальная глубина такой ямы определяется безузловой
в ![]() -направлении собственной функцией
-направлении собственной функцией
Исследуем дисперсионные свойства возмущений, описываемых
уравнением (2.80), частота которых в системе
отсчета, вращающейся вместе с веществом диска, меньше
эпициклической (
![]() ). Для
приближенного вычисления этих частот в (2.80)
можно опустить члены ряда с
). Для
приближенного вычисления этих частот в (2.80)
можно опустить члены ряда с ![]() . Упрощенное таким образом
дисперсионное уравнение приобретает вид
. Упрощенное таким образом
дисперсионное уравнение приобретает вид
Если рассматривать только осесимметричные возмущения (![]() и,
следовательно,
и,
следовательно,
![]() ), то (2.81) описывает две гравитационные (джинсовские) ветви
колебаний звездного диска, частоты которых различаются знаком:
), то (2.81) описывает две гравитационные (джинсовские) ветви
колебаний звездного диска, частоты которых различаются знаком:
Перейдем к изучению спектра неосесимметричных возмущений.
Предварительно заметим, что
![]() . С учетом
того, что для наиболее близких к порогу неустойчивости возмущений
в маргинально устойчивом по Тоомре-Вандервоорту диске
. С учетом
того, что для наиболее близких к порогу неустойчивости возмущений
в маргинально устойчивом по Тоомре-Вандервоорту диске
![]() , а также условия (2.60) это означает, что
для таких возмущений
, а также условия (2.60) это означает, что
для таких возмущений
В длинноволновой части спектра (![]() ) в маргинально
устойчивом по Тоомре диске условие (2.86) тоже
выполняется и, следовательно, эффекты неоднородности диска малы. В
этом пределе законы дисперсии двух гравитационных ветвей колебаний
звездного диска согласно (2.81) имеют вид mm
) в маргинально
устойчивом по Тоомре диске условие (2.86) тоже
выполняется и, следовательно, эффекты неоднородности диска малы. В
этом пределе законы дисперсии двух гравитационных ветвей колебаний
звездного диска согласно (2.81) имеют вид mm
В коротковолновой же части спектра (![]() ), используя
асимптотику модифицированных функций Бесселя, из
(2.81) получим
), используя
асимптотику модифицированных функций Бесселя, из
(2.81) получим
Таким образом, как в длинноволновой, так и в коротковолновой частях
спектра градиентная ветвь ![]() является низкочастотной и
хорошо отделена от гравитационных ветвей. Все три ветви в этих частях
спектра оказываются устойчивыми в маргинально устойчивом относительно
осесимметричных возмущений диске.
является низкочастотной и
хорошо отделена от гравитационных ветвей. Все три ветви в этих частях
спектра оказываются устойчивыми в маргинально устойчивом относительно
осесимметричных возмущений диске.
Иной результат получается в промежуточной области длин волн
![]() . Чтобы продемонстрировать это, рассмотрим
простую модель тонкого (
. Чтобы продемонстрировать это, рассмотрим
простую модель тонкого (![]() ) твердотельно вращающегося
(
) твердотельно вращающегося
(
![]() ) неоднородного диска, в котором
) неоднородного диска, в котором
![]() (тем самым масштабы неоднородностей
(тем самым масштабы неоднородностей ![]() и
и ![]() одинаковы и, следовательно,
одинаковы и, следовательно,
![]() ). В
малой окрестности
). В
малой окрестности
![]() маргинально
устойчивых по Тоомре возмущений с
маргинально
устойчивых по Тоомре возмущений с ![]() [см.(2.84)] дисперсионное уравнение
(2.81) принимает вид
[см.(2.84)] дисперсионное уравнение
(2.81) принимает вид
Полагаем диск слабонеоднородным: ![]() . Тогда в главном
порядке по
. Тогда в главном
порядке по ![]() из (2.91) для частот колебаний
диска следует:
из (2.91) для частот колебаний
диска следует:
Известно, что в маргинально устойчивом по Тоомре диске в
окрестности точки ![]() частоты обеих гравитационных ветвей
осесимметричных возмущений пропорциональны
частоты обеих гравитационных ветвей
осесимметричных возмущений пропорциональны ![]() . Ясно,
что в некоторой малой (в силу
. Ясно,
что в некоторой малой (в силу
![]() )
окрестности
)
окрестности ![]() частота градиентных возмущений окажется
сравнимой с частотой одной из гравитационных ветвей
неосесимметричных возмущений. Тогда взаимовлияние этих ветвей,
искажая спектры возмущений, приведет к неустойчивости
неосесимметричных возмущений. Таким образом, причиной
гравитационно-градиентной неустойчивости (2.92)
является неоднородность диска. Природа же этой неустойчивости,
очевидно, гравитационная.
частота градиентных возмущений окажется
сравнимой с частотой одной из гравитационных ветвей
неосесимметричных возмущений. Тогда взаимовлияние этих ветвей,
искажая спектры возмущений, приведет к неустойчивости
неосесимметричных возмущений. Таким образом, причиной
гравитационно-градиентной неустойчивости (2.92)
является неоднородность диска. Природа же этой неустойчивости,
очевидно, гравитационная.
Гравитационно-градиентная неустойчивость принадлежит к типу
``абсолютных'', то есть таких, при возбуждении которых амплитуда
возмущений растет в каждой точке пространства, движущейся вместе с
веществом диска. Действительно, неустойчивость является
``абсолютной'', а не ``конвективной'' (в этом случае неустойчивое
возмущение сносится течением так быстро, что в каждой точке
пространства возмущения со временем стремятся к нулю), если
выполняется условие [67]
Впервые градиентная ветвь была получена Хантером
[500] в модели холодного (![]() ) гравитирующего диска. Описанные здесь результаты
относятся к достаточно горячему (
) гравитирующего диска. Описанные здесь результаты
относятся к достаточно горячему (
![]() )
бесстолкновительному диску. Тем не менее результат Хантера
вытекает из дисперсионного уравнения (2.80) при
выполнении цепочки неравенств
)
бесстолкновительному диску. Тем не менее результат Хантера
вытекает из дисперсионного уравнения (2.80) при
выполнении цепочки неравенств
![]() (в
реальных системах
(в
реальных системах
![]() ).
).
Главным ``возмутителем спокойствия'' в изучаемых нами дисках является гравитация. Гравитационное взаимодействие между разными частями системы (часто говорят ``самогравитация'') сжимает вещество, оно стремится упасть само на себя. Этот процесс называют гравитационной или джинсовской неустойчивостью. Он приводит к перераспределению массы -- в одной области плотность растет, в другой по необходимости уменьшается. Ряд факторов противостоит самогравитации, другие помогают ей. Прежде чем перейти в следующих разделах к строгому изложению, обсудим физику гравитационной неустойчивости, попытаемся качественно понять, как различные свойства системы влияют на стремление самогравитации ``сжать вещество в точку''. Джинсовская неустойчивость обладает схожими чертами в звездном и газовом дисках, поэтому мы рассмотрим здесь и газовую систему (см. подробнее гл. 4), тем более, что она для анализа проще. При этом нагляднее проявятся и различия между ними и выяснится, какое влияние на гравитационную устойчивость звездного диска может оказать газовая подсистема. Для нас сейчас все отличие газа от звезд заключается в столкновительности первого, тем самым он описывается уравнениями газодинамики.
Все формулы данного раздела будут получены в последующем,
поэтому сейчас укажем только основные приближения, в рамках
которых они получены. Это эпициклическое приближение (см.
(2.13)), диск считается тонким (см.
(2.11)), возмущения лежат в плоскости диска и
являются коротковолновыми (см. (2.60)). Отметим,
что все приведенные здесь соотношения для звездного диска вытекают
из дисперсионного уравнения (2.80), а для
газового
-- из (![]() ). Индексы ``
). Индексы ``![]() '', ``
'', ``![]() ''
указывают соответственно на принадлежность величины к звездному
или газовому диску. Для составления всестороннего понимания
механизма гравитационной неустойчивости рекомендуем также
обратиться к монографиям Поляченко и Фридмана
[163,
420], Рольфса
[739], Саслау
[181].
''
указывают соответственно на принадлежность величины к звездному
или газовому диску. Для составления всестороннего понимания
механизма гравитационной неустойчивости рекомендуем также
обратиться к монографиям Поляченко и Фридмана
[163,
420], Рольфса
[739], Саслау
[181].
Пренебрежем влиянием всех факторов, кроме самогравитации, то
есть рассмотрим плоский
холодный 2.9
бесконечно тонкий гравитирующий слой 2.10. В такой модели при
сжатии не возникает противодействующей силы. Вещество, ускоряясь,
падает на область повышенной плотности, все более увеличивая
величину плотности и тем самым силу притяжения. Развивается
гравитационная неустойчивость (коллапс), частота возмущений
которой является чисто мнимой
Ниже мы будем последовательно включать в рассмотрение учет хаотического движения частиц, вращения диска, различных неоднородностей равновесных величин и т. п. Некоторые факторы делают диск более неустойчивым (увеличивают инкремент), и их естественно называть дестабилизирующими. Другие приводят к уменьшению инкремента вплоть до стабилизации гравитационной неустойчивости.
Как хорошо известно, если рассмотренные выше две
гравитационно взаимодействующие частицы обладают моментом
количества движения (первоначально движутся не вдоль одной
прямой), то такое относительное ``случайное'' движение может
предотвратить столкновение. При переходе к системе с большим
количеством частиц роль этих случайных движений выполняет тепловое
движение (``температура''), и оно работает против гравитационного
скучивания. Если возникает область повышенной плотности размером
![]() , то звезды за счет случайного движения могут
покинуть опасную зону, уменьшить плотность в ней и тем самым
остановить падение окружающего вещества. Условием устойчивости
является превышение типичной скорости звезды
, то звезды за счет случайного движения могут
покинуть опасную зону, уменьшить плотность в ней и тем самым
остановить падение окружающего вещества. Условием устойчивости
является превышение типичной скорости звезды ![]() над характерной
скоростью гравитационного падения
над характерной
скоростью гравитационного падения
![]() , что приводит к требованию
, что приводит к требованию
![]() . Естественно, малое по размеру возмущение легче
стабилизируется хаотическим движением. В случае газа аналогичную
оценку можно получить из условия равенства характерного времени
гравитационного падения и времени прохождения через область
размером
. Естественно, малое по размеру возмущение легче
стабилизируется хаотическим движением. В случае газа аналогичную
оценку можно получить из условия равенства характерного времени
гравитационного падения и времени прохождения через область
размером
![]() звуковой волны в газе. При
возникновении сжатия начинает распространяться звуковая волна.
Если характерное время гравитационного нарастания
звуковой волны в газе. При
возникновении сжатия начинает распространяться звуковая волна.
Если характерное время гравитационного нарастания ![]() превышает
период колебаний
превышает
период колебаний
![]() , то возмущения
устойчивы: на быстро движущуюся волну вещество падать не
успевает. Опираясь на эту оценку, можно попытаться обобщить
(2.95) на случай конечных значений
, то возмущения
устойчивы: на быстро движущуюся волну вещество падать не
успевает. Опираясь на эту оценку, можно попытаться обобщить
(2.95) на случай конечных значений ![]() :
:
Учет вращения трансформирует плоский слой в собственно диск и
делает устойчивыми длинноволновые осесимметричные (![]() ) возмущения. Это легко понять из следующих
рассуждений. Если область размером
) возмущения. Это легко понять из следующих
рассуждений. Если область размером
![]() твердотельно вращающегося с угловой скоростью
твердотельно вращающегося с угловой скоростью ![]() однородного диска сжать на
однородного диска сжать на
![]() , то в силу
закона сохранения момента импульса вещество на радиусе (
, то в силу
закона сохранения момента импульса вещество на радиусе (
![]() ) будет вращаться с
) будет вращаться с
![]() . В результате появляется возвращающая центробежная сила
. В результате появляется возвращающая центробежная сила
![]() с точностью до малого
с точностью до малого
![]() .
Если мы сравним ее с дополнительной гравитационной силой
притяжения, связанной со сжатием диска
.
Если мы сравним ее с дополнительной гравитационной силой
притяжения, связанной со сжатием диска
![]() , то увидим, что
устойчивы будут только крупномасштабные возмущения
, то увидим, что
устойчивы будут только крупномасштабные возмущения
![]() . Дисперсионное соотношение
для звуковых волн во вращающейся среде имеет вид
. Дисперсионное соотношение
для звуковых волн во вращающейся среде имеет вид
![]() (первое слагаемое описывает
эпициклические колебания), и уравнения (2.95),
(2.96) можно обобщить:
(первое слагаемое описывает
эпициклические колебания), и уравнения (2.95),
(2.96) можно обобщить:
=0.34 |
Хотя для бесстолкновительного звездного диска дисперсионное
уравнение имеет более сложный вид, условие устойчивости мало
отличается от случая газового диска. На
рис. 2.1![]() в,
в,![]() г показаны две
джинсовские ветви в области
г показаны две
джинсовские ветви в области
![]() 2.11. Они аналогичны гравитационным ветвям газового
диска (рис. 2.1
2.11. Они аналогичны гравитационным ветвям газового
диска (рис. 2.1![]() а,
а,![]() б), но их
поведение различается в области малых длин волн. Различие
связано с особенностями хаотического движения в столкновительной
и бесстолкновительной системах. В первой возникают звуковые
волны, во второй для мелкомасштабных возмущений случайное
движение не приводит к волновому процессу, и закон дисперсии
определяется вращением
б), но их
поведение различается в области малых длин волн. Различие
связано с особенностями хаотического движения в столкновительной
и бесстолкновительной системах. В первой возникают звуковые
волны, во второй для мелкомасштабных возмущений случайное
движение не приводит к волновому процессу, и закон дисперсии
определяется вращением
![]() . Как мы
знаем, в системе отсчета, вращающейся с угловой скоростью
. Как мы
знаем, в системе отсчета, вращающейся с угловой скоростью
![]() , траектория движения звезды в модели твердотельно
вращающегося диска представляет собой окружность с характерным
эпициклическим радиусом
, траектория движения звезды в модели твердотельно
вращающегося диска представляет собой окружность с характерным
эпициклическим радиусом
![]() (см.
п. 1.1.3). Поэтому только возмущения с
(см.
п. 1.1.3). Поэтому только возмущения с
![]() испытывают значительное влияние случайного движения
звезд.
испытывают значительное влияние случайного движения
звезд.
В случае бесстолкновительного диска роль параметра ![]() играет
паpаметp Тоомpе
играет
паpаметp Тоомpе
![]() [851], и для устойчивости
необходимо
[851], и для устойчивости
необходимо
![]() . Волновое число удобно
нормировать на величину
. Волновое число удобно
нормировать на величину ![]() (
(
![]() --
эпициклический радиус при
--
эпициклический радиус при ![]() ). Тогда на границе
устойчивости (
). Тогда на границе
устойчивости (
![]() ,
, ![]() ) находятся волны с
) находятся волны с
![]() (см.
рис. 2.1
(см.
рис. 2.1![]() в). При
в). При ![]() , как и
в случае газового диска, возмущения с
, как и
в случае газового диска, возмущения с ![]() оказываются
абсолютно неустойчивыми, поскольку для них
оказываются
абсолютно неустойчивыми, поскольку для них
![]() (рис. 2.1
(рис. 2.1![]() г). Заметим,
что поскольку в галактиках
г). Заметим,
что поскольку в галактиках
![]() , то
, то
![]() .
.
Устойчивость звездных и газовых дисков определяется
значениями параметров
![]() и
и
![]() соответственно, которые формально
совпадают с точностью до числового коэффициента. Замена
соответственно, которые формально
совпадают с точностью до числового коэффициента. Замена ![]() на
на
![]() обусловлена бесстолкновительностью системы и конкретным
выбором функции распределения звезд по скоростям
обусловлена бесстолкновительностью системы и конкретным
выбором функции распределения звезд по скоростям ![]() (2.32). Как уже упоминалось, функция вида
(2.32) описывает реальные распределения скоростей
звезд приближенно [30,
107, 223,
224]. Связано это со звездообразованием,
усиливающимся при прохождении спиральной волны плотности,
бесстолкновительностью системы в смысле звездно-звездного
взаимодействия (проблема релаксации и начальных условий) и, как
следствие, с дискретностью звездного населения по кинематике.
Построение функции распределения
(2.32). Как уже упоминалось, функция вида
(2.32) описывает реальные распределения скоростей
звезд приближенно [30,
107, 223,
224]. Связано это со звездообразованием,
усиливающимся при прохождении спиральной волны плотности,
бесстолкновительностью системы в смысле звездно-звездного
взаимодействия (проблема релаксации и начальных условий) и, как
следствие, с дискретностью звездного населения по кинематике.
Построение функции распределения ![]() непосредственно из
наблюдений в солнечной окрестности Галактики дает систематическое
отклонение от (2.32) [223,
224]. Как и ранее, считаем диск бесконечно тонким
и однородным. По определению, функция распределения удовлетворяет
условиям:
непосредственно из
наблюдений в солнечной окрестности Галактики дает систематическое
отклонение от (2.32) [223,
224]. Как и ранее, считаем диск бесконечно тонким
и однородным. По определению, функция распределения удовлетворяет
условиям:
=0.435 |
Одну и ту же дисперсию скоростей можно создать
различным распределением скоростей. Обсудим, как могут повлиять
возможные отклонения функции распределения от шварцшильдовской
![]() (2.32). На
рис. 2.2
(2.32). На
рис. 2.2![]() а изображены два качественно
разных случая, различающихся избытком медленных звезд
а изображены два качественно
разных случая, различающихся избытком медленных звезд ![]() и их
недостатком
и их
недостатком ![]() в сравнении с функцией
в сравнении с функцией ![]() . Во всех трех
случаях величина
. Во всех трех
случаях величина ![]() по (2.99) одна и та же.
Для гравитационной устойчивости модели с
по (2.99) одна и та же.
Для гравитационной устойчивости модели с ![]() , чтобы
стабилизировать подсистему медленных частиц, требуется в целом
сильнее разогреть систему, то есть минимально необходимая для
устойчивости дисперсия скоростей
, чтобы
стабилизировать подсистему медленных частиц, требуется в целом
сильнее разогреть систему, то есть минимально необходимая для
устойчивости дисперсия скоростей ![]() должна превышать
должна превышать
![]() . В случае с
. В случае с ![]() для устойчивости будет достаточно
для устойчивости будет достаточно
![]() .
.
Звездное население дисков плоских галактик можно разбить на ![]() подсистем, каждая из которых характеризуется своей поверхностной
плотностью
подсистем, каждая из которых характеризуется своей поверхностной
плотностью ![]() и дисперсией
и дисперсией ![]() , так что в силу
(2.99)
, так что в силу
(2.99)
Предположим, что каждая подсистема описывается
шварцшильдовским распределением
![]() . На
рис. 2.2
. На
рис. 2.2![]() б показаны функции
распределения длины вектора скорости
для
б показаны функции
распределения длины вектора скорости
для ![]() ,
, ![]() пpи различных отношениях
пpи различных отношениях ![]() и
и ![]() .
Под холодной и маломассивной подсистемой (
.
Под холодной и маломассивной подсистемой (![]() и
и ![]() ) можно понимать молодые звезды. Для гравитационной
стабилизации такой модели необходимо в целом сильнее
разогреть систему
) можно понимать молодые звезды. Для гравитационной
стабилизации такой модели необходимо в целом сильнее
разогреть систему
![]() . Очевидно, что при любое соотношение наборов
. Очевидно, что при любое соотношение наборов ![]() ,
, ![]() (естественно,
удовлетворяющих условиям (2.100)) дает более
неустойчивый диск по сравнению с
(естественно,
удовлетворяющих условиям (2.100)) дает более
неустойчивый диск по сравнению с ![]() , поскольку в таких
моделях всегда имеется избыток холодных звезд.
Расчеты с наблюдаемой функцией распределения скоростей звезд
вблизи Солнца говорят о том, что поправка эта невелика и
составляет не более 15 %.
, поскольку в таких
моделях всегда имеется избыток холодных звезд.
Расчеты с наблюдаемой функцией распределения скоростей звезд
вблизи Солнца говорят о том, что поправка эта невелика и
составляет не более 15 %.
В рамках обсуждаемого здесь подхода рассмотрим
звездно-газовый диск. Характерная скорость газовых облаков ![]() существенно меньше дисперсии скоростей звезд
существенно меньше дисперсии скоростей звезд ![]() . Кроме того,
. Кроме того,
![]() . С этой точки зрения учет газовой подсистемы
эквивалентен наличию молодых звезд, что, как мы видели, является
дестабилизирующим фактором (см.
подробнее п. 5.1.1).
. С этой точки зрения учет газовой подсистемы
эквивалентен наличию молодых звезд, что, как мы видели, является
дестабилизирующим фактором (см.
подробнее п. 5.1.1).
Чтобы ответить на принципиальный вопрос о том, является
конечная толщина диска ![]() стабилизирующим или
дестабилизирующим фактором, обратимся к уравнению
(2.95) и запишем его в виде
стабилизирующим или
дестабилизирующим фактором, обратимся к уравнению
(2.95) и запишем его в виде
![]() , где средняя плотность
, где средняя плотность
![]() . Естественно, оно справедливо только в
пределе
. Естественно, оно справедливо только в
пределе
![]() . Мы показали в п. 2.3.1, что
в обратном пределе
. Мы показали в п. 2.3.1, что
в обратном пределе
![]() справедливо
справедливо
![]() . Как видно из
рис. 2.3, следует ожидать
стабилизирующего влияния толщины диска на его гравитационную
устойчивость. Действительно, величина
. Как видно из
рис. 2.3, следует ожидать
стабилизирующего влияния толщины диска на его гравитационную
устойчивость. Действительно, величина ![]() и поверхностная
плотность
и поверхностная
плотность ![]() входят в дисперсионное уравнение
(2.80) только в комбинации
входят в дисперсионное уравнение
(2.80) только в комбинации
![]() , что уменьшает инкремент при
, что уменьшает инкремент при
![]() .
Поскольку наиболее неустойчивые возмущения обладают
.
Поскольку наиболее неустойчивые возмущения обладают
![]() , можно обобщить критерий устойчивости звездного
диска с учетом
, можно обобщить критерий устойчивости звездного
диска с учетом ![]() и записать
и записать
Выше рассматривались осесимметричные колебания ![]() , что
оправданно для однородного твердотельно вращающегося диска,
поскольку учет неосесимметричных возмущений [
, что
оправданно для однородного твердотельно вращающегося диска,
поскольку учет неосесимметричных возмущений [
![]() ] приводит только к
допплеровскому сдвигу частоты
] приводит только к
допплеровскому сдвигу частоты
![]() и не сказывается на устойчивости. В
дифференциально вращающемся диске с
и не сказывается на устойчивости. В
дифференциально вращающемся диске с ![]() осесимметричные
возмущения описываются дисперсионным уравнением
(2.97) для
осесимметричные
возмущения описываются дисперсионным уравнением
(2.97) для
![]() . Существеннее другое. Зависимость угловой
скорости от
. Существеннее другое. Зависимость угловой
скорости от ![]() приводит к тому, что более неустойчивыми
становятся неосесимметричные (``косые'') возмущения (
приводит к тому, что более неустойчивыми
становятся неосесимметричные (``косые'') возмущения (
![]() ). Рассмотрим физику этого эффекта отдельно для
звездного и газового дисков.
). Рассмотрим физику этого эффекта отдельно для
звездного и газового дисков.
При построении равновесной модели звездного диска в
п. 2.1.2 мы получили
![]() , и
для угловой скорости вращения
, и
для угловой скорости вращения ![]() , убывающей с радиусом,
выполняется
, убывающей с радиусом,
выполняется
![]() . С учетом дифференциальности
вращения, траектория движения звезды становится эллипсом с
характерными масштабами осей
. С учетом дифференциальности
вращения, траектория движения звезды становится эллипсом с
характерными масштабами осей
![]() и
и
![]() (рис. 2.4).
При движении по эллипсу в среднем скорость
звезды в азимутальном направлении меньше, чем в радиальном, и
неосесимметричные возмущения (в пределе ``спицеобразные'') труднее
подавить по сравнению с осесимметричными. Дисперсия азимутальных
скоростей определяет упругость среды для косых возмущений, и для
подавления гравитационной неустойчивости необходимо в
(рис. 2.4).
При движении по эллипсу в среднем скорость
звезды в азимутальном направлении меньше, чем в радиальном, и
неосесимметричные возмущения (в пределе ``спицеобразные'') труднее
подавить по сравнению с осесимметричными. Дисперсия азимутальных
скоростей определяет упругость среды для косых возмущений, и для
подавления гравитационной неустойчивости необходимо в
![]() раз сильнее разогреть диск. Таким образом,
устойчивость определяется меньшей из величин
раз сильнее разогреть диск. Таким образом,
устойчивость определяется меньшей из величин ![]() и
и ![]() :
:
Рассмотрим газовый диск. Из-за столкновительности
``макромолекулы'' газа не движутся по эпициклам, и давление
является изотропным в радиальном и азимутальном
направлениях. Дестабилизирующее влияние дифференциальности
вращения связано с действием двух факторов. Во-первых,
меняется закон дисперсии неосесимметричных звуковых волн
(2.97). Этот эффект связан с действием силы
Кориолиса. Косые возмущения вызывают радиальную компоненту силы
Кориолиса, причем в первом порядке по дифференциальности
вращения она не зависит от знака ![]() ; поэтому в
дисперсионное уравнение должна входить величина
; поэтому в
дисперсионное уравнение должна входить величина ![]() .
Вычисления дают
.
Вычисления дают
Для плоской кривой вращения (![]() ) имеем
) имеем
![]() (аналогичный результат получен в работе
[174]). Оба условия
(2.102) и (2.104) при
(аналогичный результат получен в работе
[174]). Оба условия
(2.102) и (2.104) при
![]() дают бесконечно большие значения параметра
дают бесконечно большие значения параметра ![]() ,
что связано с неустойчивостью круговых орбит для закона с
,
что связано с неустойчивостью круговых орбит для закона с ![]() . Эта неустойчивость обусловлена видом внешнего потенциала, не
связана с самогравитацией и не может быть подавлена температурой.
Следует сказать, что для систем с
. Эта неустойчивость обусловлена видом внешнего потенциала, не
связана с самогравитацией и не может быть подавлена температурой.
Следует сказать, что для систем с ![]() из-за
нарушения условий, положенных в основу получения данных критериев,
погрешность этих формул может быть
существенной 2.12.
из-за
нарушения условий, положенных в основу получения данных критериев,
погрешность этих формул может быть
существенной 2.12.
Имеется еще один дестабилизирующий фактор, связанный с дифференциальностью вращения, однако рассмотрение его более естественно провести в следующем пункте.
Под неоднородностью диска мы будем понимать зависимость
поверхностной плотности и/или дисперсии скоростей (скорости звука
для газового диска) от радиальной координаты. В однородной системе
имеются две джинсовские ветви колебаний (см.
рис. 2.1). Неоднородность диска (или
дифференциальность вращения) приводит к появлению еще одной ветви
колебаний, ее называют градиентной. Волновой вектор ![]() для
этого типа колебаний должен быть направлен под углом к градиенту
равновесной величины. Как правило, чем более косые возмущения, тем
больше частота колебаний. Градиентные волны обусловлены
дополнительной ``упругостью'' неоднородной среды. Известно
множество примеров проявления таких колебаний в самых разных
областях физики.
для
этого типа колебаний должен быть направлен под углом к градиенту
равновесной величины. Как правило, чем более косые возмущения, тем
больше частота колебаний. Градиентные волны обусловлены
дополнительной ``упругостью'' неоднородной среды. Известно
множество примеров проявления таких колебаний в самых разных
областях физики.
Поверхностные гравитационные волны на поверхности
раздела двух сред (ПГВ) -- наиболее известный тип
волн, связанный с неоднородностью системы, которая
вызвана вертикальной силой тяжести ![]() . Для несжимаемых
жидкостей с плотностью
. Для несжимаемых
жидкостей с плотностью ![]() и
и ![]() закон
дисперсии имеет вид
закон
дисперсии имеет вид
![]() .
.
Внутренние гравитационные волны (ВГВ) могут
распространяться в океане или атмосфере Земли из-за
неоднородности в вертикальном направлении объемной
плотности вещества ![]() . Для них
. Для них
Гравитационно-гироскопические волны (ГГВ) являются
примером крупномасштабных возмущений в океане постоянной
глубины ![]() с учетом вращения планеты с угловой скоростью
с учетом вращения планеты с угловой скоростью
![]() . Дисперсионное уравнение для них имеет вид
. Дисперсионное уравнение для них имеет вид
![]() , здесь . Из условия равновесия
, здесь . Из условия равновесия
![]() .
.
Волны Россби связаны с изменением
![]() вдоль географической широты
(рис. 2.5):
вдоль географической широты
(рис. 2.5):
![]() , где
, где
![]() ,
,
![]() . Возвращающей силой является сила Кориолиса.
. Возвращающей силой является сила Кориолиса.
Все эти примеры хорошо известны и легко наблюдаются в природе. Огромное количество волн градиентного типа получено при изучении физики плазмы (их часто называют желобковыми, диффузионными). Таким образом, наличие в неоднородных астрофизических дисках градиентных ветвей колебаний представляется естественным.
Рассмотрение механизма дестабилизирующего влияния
неоднородности для звездного и газового дисков дает качественно
похожие картины. На основе вышеперечисленных примеров видно, что
частота коротковолновых градиентных колебаний приближенно равна
![]() (
(![]() -- характерная скорость хаотических движений,
-- характерная скорость хаотических движений, ![]() -- характерный масштаб неоднородности), то есть они
являются низкочастотными,
-- характерный масштаб неоднородности), то есть они
являются низкочастотными,
![]() .
Если в какой-то области длин волн две ветви колебаний имеют
близкие друг другу вещественные частоты, то возможно
возникновение между ними ``слабой связи'' с появлением
Im
.
Если в какой-то области длин волн две ветви колебаний имеют
близкие друг другу вещественные частоты, то возможно
возникновение между ними ``слабой связи'' с появлением
Im
![]() , то есть неустойчивости (см., например,
[97]). В случае
гравитационно устойчивого диска с
, то есть неустойчивости (см., например,
[97]). В случае
гравитационно устойчивого диска с ![]() джинсовские и
градиентная ветвь отделены друг от друга
(рис. 2.6
джинсовские и
градиентная ветвь отделены друг от друга
(рис. 2.6![]() а). При уменьшении
параметра
а). При уменьшении
параметра ![]() частота гравитационных ветвей уменьшается, и при
некоторых
частота гравитационных ветвей уменьшается, и при
некоторых ![]() в случае
в случае
![]() отрицательная
джинсовская ветвь начинает взаимодействовать с градиентной, в
результате вместо двух действительных частот появляется два
комплексно-сопряженных
(рис. 2.6
отрицательная
джинсовская ветвь начинает взаимодействовать с градиентной, в
результате вместо двух действительных частот появляется два
комплексно-сопряженных
(рис. 2.6![]() б). Решение с
Im
соответствует гравитационно-градиентной
неустойчивости. Градиентная ветвь может при определенных условиях
взаимодействовать и/или с положительной джинсовской
(рис. 2.6
б). Решение с
Im
соответствует гравитационно-градиентной
неустойчивости. Градиентная ветвь может при определенных условиях
взаимодействовать и/или с положительной джинсовской
(рис. 2.6![]() в). Градиентные
колебания могут быть обусловлены не только неоднородностью, но и
дифференциальным вращением. Это ярко видно на приведенном выше
примере волн Россби для газа.
в). Градиентные
колебания могут быть обусловлены не только неоднородностью, но и
дифференциальным вращением. Это ярко видно на приведенном выше
примере волн Россби для газа.
=0.45 |
Для газового диска при типичных условиях дестабилизация
системы за счет эффектов взаимодействия градиентной и джинсовских
колебаний невелика. Условие (2.104) принимает вид
Для звездного диска с учетом всех рассмотренных нами
факторов запишем аналогичное условие
В заключение отметим, что в газовом диске может
существовать еще одна ветвь колебаний -- энтропийная. В
модели с равновесной энтропией
![]() const
частота этих колебаний
const
частота этих колебаний
![]() . Если
. Если
![]() , то это приводит к новой энтропийной ветви колебаний.
Естественно, она относится к градиентному типу и
является низкочастотной. Ее взаимодействие с джинсовскими
ветвями вносит дополнительное дестабилизирующее влияние.
, то это приводит к новой энтропийной ветви колебаний.
Естественно, она относится к градиентному типу и
является низкочастотной. Ее взаимодействие с джинсовскими
ветвями вносит дополнительное дестабилизирующее влияние.
Гравитационная устойчивость плоских систем относительно
мелкомасштабных возмущений определяется действием разнообразных
факторов. Примечательно, что критерий локальной устойчивости можно
записать в виде достаточно простого условия
![]() [см. (2.105),
(2.106)]. Значение параметра
[см. (2.105),
(2.106)]. Значение параметра
![]() является ключевым для рассматриваемой проблемы. Совместное
действие самогравитации, вращения и хаотического движения частиц
требует
является ключевым для рассматриваемой проблемы. Совместное
действие самогравитации, вращения и хаотического движения частиц
требует
![]() . Конечная толщина диска уменьшает
это значение, а зависимости равновесных величин от радиальной
координаты в целом приводят к
. Конечная толщина диска уменьшает
это значение, а зависимости равновесных величин от радиальной
координаты в целом приводят к
![]() . Для примера
рассмотрим солнечную окрестность звездного диска Галактики. Для
оценок примем:
. Для примера
рассмотрим солнечную окрестность звездного диска Галактики. Для
оценок примем:
![]() /пк
/пк![]() ,
, ![]() км/с кпк,
км/с кпк,
![]() ,
, ![]() пк,
пк, ![]() кпк,
кпк, ![]() кпк и, следовательно,
кпк и, следовательно, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() км/с.
Подставляя значения этих параметров в (2.106),
получим
км/с.
Подставляя значения этих параметров в (2.106),
получим
![]() .
.
Из приведенных выше результатов следует, что для устойчивости
звездного диска величина дисперсии радиальных скоростей звезд
должна превышать некоторое критическое значение. Впервые
минимально необходимую для устойчивости тонкого (![]() )
диска относительно осесимметричных возмущений величину
)
диска относительно осесимметричных возмущений величину
![]() (см. (2.83)) вычислил Тоомре
[851]. Позднее Вандервоортом
[866] эта величина была
скорректирована с учетом конечной толщины диска
(см. (2.83)) вычислил Тоомре
[851]. Позднее Вандервоортом
[866] эта величина была
скорректирована с учетом конечной толщины диска
![]() (2.85). Данные наблюдений
[156,
897] показывают, что в окрестности Солнца
(2.85). Данные наблюдений
[156,
897] показывают, что в окрестности Солнца
![]() , поэтому следует ожидать, что условие устойчивости
(2.85) является необходимым.
, поэтому следует ожидать, что условие устойчивости
(2.85) является необходимым.
Однако начатые в 70-х годах численные эксперименты
[129,
130,
379,
487,
488,
629,
630, 631,
634,
685,
782] показывают, что звездные
диски с начальным значением
![]() за
промежуток времени порядка всего лишь одного-двух оборотов диска
разогреваются до состояния с
за
промежуток времени порядка всего лишь одного-двух оборотов диска
разогреваются до состояния с
![]() . Эти результаты подтверждают необходимость условия
устойчивости звездного диска (2.85), но указывают
на его недостаточность. Поэтому обнаруженный в численных
экспериментах ``разогрев'' диска в соответствии с принципом
Ле-Шателье (см. в книге [90])
естественно трактовать как результат эволюции неустойчивой системы
к устойчивому состоянию. Следовательно, необходимо понять природу
неустойчивости, приводящей к такому разогреву.
. Эти результаты подтверждают необходимость условия
устойчивости звездного диска (2.85), но указывают
на его недостаточность. Поэтому обнаруженный в численных
экспериментах ``разогрев'' диска в соответствии с принципом
Ле-Шателье (см. в книге [90])
естественно трактовать как результат эволюции неустойчивой системы
к устойчивому состоянию. Следовательно, необходимо понять природу
неустойчивости, приводящей к такому разогреву.
Для выяснения этого вопроса в первую очередь отметим, что
равновесный бесстолкновительный диск анизотропен -- его
``упругость'' в азимутальном направлении, характеризуемая
величиной ![]() , меньше радиальной ``упругости'':
, меньше радиальной ``упругости'':
![]() , и это является
дестабилизирующим фактором. Поэтому если мы, в отличие от Тоомре
[851] и Вандервоорта
[866], исследовавших динамику
только осесимметричных возмущений, изучим поведение
неосесимметричных возмущений, то следует ожидать, что для их
стабилизации величина
, и это является
дестабилизирующим фактором. Поэтому если мы, в отличие от Тоомре
[851] и Вандервоорта
[866], исследовавших динамику
только осесимметричных возмущений, изучим поведение
неосесимметричных возмущений, то следует ожидать, что для их
стабилизации величина ![]() должна будет достичь значения,
близкого к
должна будет достичь значения,
близкого к ![]() . С учетом связи (2.34) это
означает, что величина
. С учетом связи (2.34) это
означает, что величина
![]() должна быть близка к
должна быть близка к
![]() [503].
[503].
Природа второго дестабилизирующего звездный диск фактора обусловлена, очевидно, гравитационно-градиентной неустойчивостью, интенсивность которой возрастает с ростом степени неосесимметричности возмущений. Эта неустойчивость, как будет показано ниже, тоже может быть подавлена при увеличении дисперсии радиальных скоростей звезд.
Таким образом, следует надеяться, что необходимое и достаточное условие устойчивости неоднородного дифференциально вращающегося звездного диска может быть получено как условие отсутствия комплексных корней у дисперсионного уравнения (2.80) для неосесимметричных возмущений. Такое условие в пределе однородного твердотельно вращающегося диска должно естественным образом переходить в условие (2.85).
Отметим также, что качественно эффект худшей стабилизации
неосесимметричных возмущений был известен и раньше
[146,
163,
420,
525] из исследования
устойчивости моделей звездных дисков с квадратичным потенциалом.
Однако в таких моделях градиенты плотности и дисперсии скоростей
звезд жестко связаны между собой и с другими параметрами диска, а
вращение твердотельно. Искусственность подобных моделей
подчеркивается и тем фактом, что даже невращающийся диск, то есть
диск, равновесие которого поддерживается только градиентом
``давления'' (плотности и дисперсии скоростей звезд), оказывается
гравитационно неустойчивым относительно осесимметричных
возмущений. По этой причине применимость моделей дисков с
квадратичным потенциалом к реальным галактикам весьма
проблематична. В то же время упомянутые в начале пункта численные
эксперименты, да и сам факт существования плоских галактик,
говорят о том, что вращающийся звездный диск может быть
устойчивым, и для этого в нем везде (кроме центральной части
диска) должно быть
![]() . Модель
звездного диска (2.86)-(2.88)
хорошо согласуется с данными наблюдений и поэтому попытаемся
получить условие его устойчивости из соответствующего этой модели
дисперсионного уравнения (2.80).
. Модель
звездного диска (2.86)-(2.88)
хорошо согласуется с данными наблюдений и поэтому попытаемся
получить условие его устойчивости из соответствующего этой модели
дисперсионного уравнения (2.80).
Граница устойчивости звездного диска в соответствии с приведенными
выше оценками частот градиентных возмущений должна лежать в
области частот
![]() . Поэтому
естественно использовать упрощенное дисперсионное уравнение
(2.81). Рассмотpим сначала модель одноpодного
(
. Поэтому
естественно использовать упрощенное дисперсионное уравнение
(2.81). Рассмотpим сначала модель одноpодного
(
![]() ,
, ![]() ) диска, вращающегося с
угловой скоростью, степенным образом зависящей от радиальной
координаты:
) диска, вращающегося с
угловой скоростью, степенным образом зависящей от радиальной
координаты:
![]() ,
, ![]() const
const ![]() . В этом
случае
. В этом
случае ![]() ,
, ![]() . Тем самым из рассмотрения
исключаются градиентная ветвь и связанные с ней эффекты. Уравнение
(2.81) в такой модели приобретает вид
. Тем самым из рассмотрения
исключаются градиентная ветвь и связанные с ней эффекты. Уравнение
(2.81) в такой модели приобретает вид
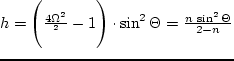 ;
;
Граница устойчивости возмущений с заданным
![]() определяется из (2.107) соотношениями
определяется из (2.107) соотношениями
![]() ;
;
![]() [
[
![]() в минимуме
дисперсионной кривой
в минимуме
дисперсионной кривой
![]() ], что
эквивалентно системе уравнений:
], что
эквивалентно системе уравнений:
Перейдем теперь к диску конечной толщины. Согласно данным
наблюдений (см. п. 1.1.4),
(2.40), (2.83), отношение
![]() . Поэтому найдем поправку
к (2.110), (2.111), связанную с
конечностью отношения
. Поэтому найдем поправку
к (2.110), (2.111), связанную с
конечностью отношения ![]() в первом порядке по этой
величине. В результате из (2.108),
(2.109) получаем [ср. с (2.85)]
в первом порядке по этой
величине. В результате из (2.108),
(2.109) получаем [ср. с (2.85)]
Определим теперь влияние неоднородности поверхностной плотности на
величину минимально необходимой дисперсии радиальных скоростей
звезд для устойчивости неосесимметричных возмущений с заданным
![]() и на длину волны маргинально устойчивых возмущений (учет
и на длину волны маргинально устойчивых возмущений (учет
![]() см. в
п. 2.4.5). В качестве
начального приближения используем модель тонкого дифференциально
вращающегося диска -- см. (2.110),
(2.111), считая, что влияние его малой толщины уже
определено мультипликативными формфакторами в
(2.112), (2.113). В этом случае в
окрестности минимума дисперсионной кривой гравитационных
возмущений (
см. в
п. 2.4.5). В качестве
начального приближения используем модель тонкого дифференциально
вращающегося диска -- см. (2.110),
(2.111), считая, что влияние его малой толщины уже
определено мультипликативными формфакторами в
(2.112), (2.113). В этом случае в
окрестности минимума дисперсионной кривой гравитационных
возмущений (![]() ) существенно влияние градиентной ветви
(см. п. 2.2.4). Поэтому условие
устойчивости такого диска должно вытекать из условия отсутствия
комплексных корней у кубического по
) существенно влияние градиентной ветви
(см. п. 2.2.4). Поэтому условие
устойчивости такого диска должно вытекать из условия отсутствия
комплексных корней у кубического по ![]() дисперсионного
уравнения (2.81). Запишем это уравнение в виде
дисперсионного
уравнения (2.81). Запишем это уравнение в виде
![]() и линейным преобразованием
и линейным преобразованием
![]() приведем к
виду
приведем к
виду
![]() . Тогда диск будет
устойчив относительно таких возмущений, для которых
. Тогда диск будет
устойчив относительно таких возмущений, для которых
![]() . При
. При
![]() как в
длинноволновой (
как в
длинноволновой (![]() ), так и в коротковолновой (
), так и в коротковолновой (![]() ) частях спектра заведомо
) частях спектра заведомо ![]() [см.
(2.87)-(2.90)]. В промежуточной
же области может быть и
[см.
(2.87)-(2.90)]. В промежуточной
же области может быть и ![]() . Таким образом,
. Таким образом, ![]() , будучи выпуклой кверху функцией, будет достигать
своего максимального значения где-то в окрестности
, будучи выпуклой кверху функцией, будет достигать
своего максимального значения где-то в окрестности
![]() . Отсюда ясно, что у (2.81) исчезнут
комплексные корни при любых
. Отсюда ясно, что у (2.81) исчезнут
комплексные корни при любых ![]() , как только будет
выполняться условие
, как только будет
выполняться условие ![]() для тех возмущений, для которых
для тех возмущений, для которых
![]() . Из системы этих двух уравнений могут быть
вычислены
. Из системы этих двух уравнений могут быть
вычислены ![]() для заданного типа возмущений и длина
волны маргинально устойчивых возмущений.
для заданного типа возмущений и длина
волны маргинально устойчивых возмущений.
Вычисления проводим в главном порядке по малому параметру
Обсудим условия применимости критерия устойчивости бесстолкновительных звездных дисков, вытекающего из дисперсионного уравнения (2.80).
Величина минимально необходимой для устойчивости дисперсии
радиальных скоростей звезд возрастает с увеличением
![]() [(
[(
![]() , см.
(2.115)]. Можно вычислить максимальное ее значение,
равное
, см.
(2.115)]. Можно вычислить максимальное ее значение,
равное
![]() , и полагать, что
устойчивость диска относительно произвольных возмущений имеет
место при
, и полагать, что
устойчивость диска относительно произвольных возмущений имеет
место при ![]() . Но в этом случае необходимо учитывать
влияние двух факторов. Во-первых, дисперсионное уравнение
(2.80) получено в рамках ВКБ-приближения. Даже
если дойти до границы применимости ВКБ-приближения (см. сноску в
п. 2.2.2), то
. Но в этом случае необходимо учитывать
влияние двух факторов. Во-первых, дисперсионное уравнение
(2.80) получено в рамках ВКБ-приближения. Даже
если дойти до границы применимости ВКБ-приближения (см. сноску в
п. 2.2.2), то
![]() .
Граница устойчивости диска лежит в области
.
Граница устойчивости диска лежит в области ![]() ,
поэтому для
,
поэтому для ![]() величина
величина
![]() и тем самым
и тем самым
![]() (в окрестности Солнца
(в окрестности Солнца
![]() ).
Во-вторых, существует более серьезное ограничение, обусловленное
дифференциальностью вращения диска. Действительно, величина
).
Во-вторых, существует более серьезное ограничение, обусловленное
дифференциальностью вращения диска. Действительно, величина
![]() изменяется вдоль радиальной
координаты. И необходимо, естественно, считать, что изменение
изменяется вдоль радиальной
координаты. И необходимо, естественно, считать, что изменение
![]() на масштабе, характеризующем изменение
возмущения вдоль радиальной координаты, должно быть мало по
сравнению с
на масштабе, характеризующем изменение
возмущения вдоль радиальной координаты, должно быть мало по
сравнению с
![]() :
:
Предположим теперь, что используем критерий устойчивости диска в
пределе
![]() . Оценим относительное изменение
величины
. Оценим относительное изменение
величины ![]() при замене
при замене
![]() на
на
![]() . Поскольку (2.117) и вытекающее из
него (2.120) получены в главном порядке по
параметру
. Поскольку (2.117) и вытекающее из
него (2.120) получены в главном порядке по
параметру ![]() , то для оценки упомянутой величины необходимо
пользоваться критерием, не учитывающим неоднородности диска
(2.110). Тогда для относительного изменения
, то для оценки упомянутой величины необходимо
пользоваться критерием, не учитывающим неоднородности диска
(2.110). Тогда для относительного изменения
![]() имеем
имеем
С другой стороны, величина дисперсии радиальных скоростей
звезд определяется из наблюдений тоже с некоторой
погрешностью
Для примера приведем решения (2.125) для значений
параметров ![]() М
М![]() /пк
/пк![]() ,
, ![]() км/с/кпк,
км/с/кпк, ![]() кпк:
кпк:
Получим теперь общее условие устойчивости звездного диска с учетом
градиента дисперсии скоростей звезд (
![]() ) и
возможного отклонения дифференциального вращения диска от
степенного закона (
) и
возможного отклонения дифференциального вращения диска от
степенного закона (![]() ). Вычисления в этом случае
аналогичны приведенным в
п. 2.4.3. Учитывая
также влияние конечной толщины диска, описываемое соотношением
(2.112), приходим к следующему результату:
). Вычисления в этом случае
аналогичны приведенным в
п. 2.4.3. Учитывая
также влияние конечной толщины диска, описываемое соотношением
(2.112), приходим к следующему результату:
Результаты проверки оценки (2.127) в численных экспериментах и для некоторых построенных моделей Галактики обсуждаются в главе 3.
При обсуждении критерия устойчивости Тоомре-Вандервоорта (см.
п. 2.3.1) уже упоминалось о численных
экспериментах с моделями звездных дисков. Эти эксперименты (см.
также гл. 3), в частности, показывают, что в процессе эволюции к
стационарному состоянию в таких моделях происходит
перераспределение равновесных поверхностной плотности ![]() и
скорости вращения
и ``разогрев'' дисков до
состояния, в котором экспериментальное значение
и
скорости вращения
и ``разогрев'' дисков до
состояния, в котором экспериментальное значение ![]() оказывается
близким к
оказывается
близким к ![]() по (2.127). В то же время
величина
по (2.127). В то же время
величина ![]() зависит не только от локальных значений
зависит не только от локальных значений
![]() ,
, ![]() , но и от их градиентов, а также от
величины градиента
, но и от их градиентов, а также от
величины градиента ![]() . Поэтому можно ожидать, что в процессе
эволюции в маргинально устойчивое состояние в звездном диске
распределения параметров станут такими, что величина
. Поэтому можно ожидать, что в процессе
эволюции в маргинально устойчивое состояние в звездном диске
распределения параметров станут такими, что величина ![]() будет близка к минимально возможной. Проанализируем с этой точки
зрения дисперсионные свойства ветвей колебаний звездного диска и
условие его гравитационной устойчивости.
будет близка к минимально возможной. Проанализируем с этой точки
зрения дисперсионные свойства ветвей колебаний звездного диска и
условие его гравитационной устойчивости.
Как мы выяснили выше, дестабилизирующее влияние радиальной
неоднородности параметров диска обусловлено двумя факторами.
Во-первых, в стационарном звездном диске для дисперсии
азимутальных скоростей звезд имеем
![]() [163], и, следовательно, для
стабилизации предельно неосесимметричных возмущений из-за меньшей,
чем радиальная, азимутальной ``упругости'' диска величина
[163], и, следовательно, для
стабилизации предельно неосесимметричных возмущений из-за меньшей,
чем радиальная, азимутальной ``упругости'' диска величина ![]() должна быть в
должна быть в
![]() раз больше, чем
раз больше, чем ![]() .
Во-вторых, дисперсионное уравнение (2.80) в
области частот
.
Во-вторых, дисперсионное уравнение (2.80) в
области частот
![]() описывает три
ветви колебаний в плоскости диска: две гравитационные и одну
градиентную. Градиентная ветвь обусловлена наличием неоднородности
дисперсии радиальных скоростей звезд или неоднородности
поверхностной плотности диска, либо и тем, и другим.
Дополнительная дестабилизация возмущений в неоднородном диске
связана с возникновением ``взаимодействия'' между градиентной и
гравитационными ветвями в случае недостаточно горячего (
описывает три
ветви колебаний в плоскости диска: две гравитационные и одну
градиентную. Градиентная ветвь обусловлена наличием неоднородности
дисперсии радиальных скоростей звезд или неоднородности
поверхностной плотности диска, либо и тем, и другим.
Дополнительная дестабилизация возмущений в неоднородном диске
связана с возникновением ``взаимодействия'' между градиентной и
гравитационными ветвями в случае недостаточно горячего (
![]() ) звездного диска. Ниже будем полагать закон вращения
степенным
) звездного диска. Ниже будем полагать закон вращения
степенным
![]() с
с ![]() const (
const (![]() ).
Дисперсионные кривые в области частот
).
Дисперсионные кривые в области частот
![]() в диске с
в диске с
![]() изображены на
рисунках 2.6,
2.7.
изображены на
рисунках 2.6,
2.7.
=0.52 |
В то же время с ростом ``температуры'' диска (увеличением
параметра ![]() ) абсолютная величина частоты гравитационных
возмущений в области
) абсолютная величина частоты гравитационных
возмущений в области ![]() растет, и при некотором
растет, и при некотором
![]() ``слабая связь'' градиентной и гравитационных ветвей
исчезает. Это и приводит к стабилизации гравитационно-градиентной
неустойчивости диска (см.
рис. 2.7
``слабая связь'' градиентной и гравитационных ветвей
исчезает. Это и приводит к стабилизации гравитационно-градиентной
неустойчивости диска (см.
рис. 2.7![]() б). Как видно из
рис. 2.7
б). Как видно из
рис. 2.7![]() а, в недостаточно
горячем (
а, в недостаточно
горячем (
![]() ) звездном диске в пространстве волновых
чисел могут существовать две области неустойчивости. Этот эффект
обусловлен следующим обстоятельством. Закон дисперсии градиентной
ветви колебаний диска, близкого к границе устойчивости, в области
длин волн
) звездном диске в пространстве волновых
чисел могут существовать две области неустойчивости. Этот эффект
обусловлен следующим обстоятельством. Закон дисперсии градиентной
ветви колебаний диска, близкого к границе устойчивости, в области
длин волн ![]() запишем в виде
запишем в виде
Если параметры диска таковы, что
![]() (
(![]() const), то существует лишь одна область неустойчивости в
const), то существует лишь одна область неустойчивости в ![]() -пространстве. При
-пространстве. При ![]() могут существовать две области
неустойчивости в
могут существовать две области
неустойчивости в ![]() -пространстве. И в зависимости от
параметра
-пространстве. И в зависимости от
параметра ![]() с ростом величины
с ростом величины ![]() одна из них исчезает при
меньших значениях
одна из них исчезает при
меньших значениях ![]() , а другая -- при больших. В дисках с
, а другая -- при больших. В дисках с
![]() неустойчивость в области II
подавляется при меньших значениях
неустойчивость в области II
подавляется при меньших значениях ![]() , чем неустойчивость в
области I. Если же в звездном диске
, чем неустойчивость в
области I. Если же в звездном диске
![]() , то при
меньших значениях
, то при
меньших значениях ![]() подавляется неустойчивость в области I. В
дисках с
подавляется неустойчивость в области I. В
дисках с
![]() обе области неустойчивости
исчезают практически при одном и том же значении величины
обе области неустойчивости
исчезают практически при одном и том же значении величины ![]() (рис. 2.7
(рис. 2.7![]() б). Точное
значение
б). Точное
значение ![]() , вычисленное из полного дисперсионного
уравнения (2.80), слабо зависит от параметров
диска [141].
, вычисленное из полного дисперсионного
уравнения (2.80), слабо зависит от параметров
диска [141].
Итак, функция ![]() в случае
в случае
![]() достигает своего минимума при
достигает своего минимума при
![]() . Казалось бы, в каждой
точке
. Казалось бы, в каждой
точке ![]() звездному диску ``выгодно'' иметь близкие
значения
звездному диску ``выгодно'' иметь близкие
значения ![]() и
и ![]() . Но этот вывод основывается на
локальном анализе при фиксированном
. Но этот вывод основывается на
локальном анализе при фиксированном ![]() , и, таким образом,
одновременное выполнение двух условий -- диск маргинально
устойчив и параметр
, и, таким образом,
одновременное выполнение двух условий -- диск маргинально
устойчив и параметр ![]() const
const ![]() -- в общем
случае не может реализоваться для достаточно протяженной
области.
-- в общем
случае не может реализоваться для достаточно протяженной
области.
Выясним, к чему приводит требование, чтобы весь диск (за
исключением центральных областей) обладал минимально возможной для
устойчивости дисперсией радиальных скоростей звезд
[111].
Ограничиваясь качественным рассмотрением, воспользуемся для
анализа критерием устойчивости (2.127), записанным
в форме
Численное интегрирование уравнения (2.130)
приводит к следующему результату: ограниченные решения уравнения
(2.130) возможны только при знаке ``![]() '', то есть
'', то есть
![]() . Таким образом, хотя параметр
. Таким образом, хотя параметр ![]() может зависеть
от радиальной координаты, но
может зависеть
от радиальной координаты, но
![]() .
.
Наблюдения. Величины ![]() и
и ![]() (но не сама
плотность) определяются из наблюдений достаточно уверенно. Для
ряда галактик определены дисперсии радиальных скоростей в
нескольких точках (для определения величины
(но не сама
плотность) определяются из наблюдений достаточно уверенно. Для
ряда галактик определены дисперсии радиальных скоростей в
нескольких точках (для определения величины ![]() достаточно двух)
по радиальной координате. Поэтому представляет интерес проверить
для этих объектов выполнение условия
достаточно двух)
по радиальной координате. Поэтому представляет интерес проверить
для этих объектов выполнение условия ![]() , которое
эквивалентно
, которое
эквивалентно
Для солнечной окрестности Галактики разброс значений
параметров ![]() ,
, ![]() достаточно велик:
достаточно велик: ![]() кпк,
кпк,
![]() [676];
[676];
![]() кпк
(§ 1.1, 3.6);
кпк
(§ 1.1, 3.6);
![]() кпк
[384,
867];
кпк
[384,
867];
![]() кпк [667].
Крайние оценки дают
кпк [667].
Крайние оценки дают
![]() . Условие
(2.131) выполняется и для всех 11 галактик,
рассмотренных в работе
[111], причем для
них
. Условие
(2.131) выполняется и для всех 11 галактик,
рассмотренных в работе
[111], причем для
них
![]() .
.
Следует отметить, что если в звездном диске существенную роль
играют какие-либо процессы, приводящие к нагреву диска, то система
обладает запасом устойчивости (
![]() ), и, таким
образом, условие (2.131) может нарушаться. Чтобы
установить величину
), и, таким
образом, условие (2.131) может нарушаться. Чтобы
установить величину ![]() из наблюдений, необходимо независимое
определение плотности вещества звездного диска, что является
непростой задачей.
из наблюдений, необходимо независимое
определение плотности вещества звездного диска, что является
непростой задачей.
При проведении численных экспериментов по моделированию
бесстолкновительного звездного диска можно определять
радиальные зависимости равновесных параметров ![]() ,
,
![]() ,
, ![]() ,
, ![]() и таким образом
вычислять характерные масштабы неоднородностей этих
величин (гл. 3). Результаты этих работ также подтверждают, что вне центральных
областей характерный масштаб неоднородности поверхностной
плотности не превышает по величине характерный масштаб
неоднородности дисперсии радиальных скоростей звезд (
и таким образом
вычислять характерные масштабы неоднородностей этих
величин (гл. 3). Результаты этих работ также подтверждают, что вне центральных
областей характерный масштаб неоднородности поверхностной
плотности не превышает по величине характерный масштаб
неоднородности дисперсии радиальных скоростей звезд (
![]() ). Как мы увидели выше, этот результат можно
объяснить, исходя из требования, чтобы весь диск находился на
границе гравитационной устойчивости.
). Как мы увидели выше, этот результат можно
объяснить, исходя из требования, чтобы весь диск находился на
границе гравитационной устойчивости.
Интересно также отметить, что в модели Галактики Рольфса и
Крейчмана [741] по результатам
вычисления ![]() величина
величина
![]() , а в модели
Калдвелла и Острайкера [334]
, а в модели
Калдвелла и Острайкера [334]
![]() .
.
В предыдущих разделах были изучены динамика возмущений в плоскости звездного диска и вытекающие из требования устойчивости таких возмущений ограничения на параметры диска. В этом разделе мы остановимся на другом типе возмущений -- изгибающих плоскость звездного диска -- и соответственно найдем те ограничения на параметры диска и системы в целом, которые вытекают из условия устойчивости таких возмущений.
Впервые, по-видимому, динамика изгибных (мембранных) колебаний в
моделях холодных тонких дисков была рассмотрена в работе Хантера и
Тоомре [501]. Это
исследование имело целью объяснение наблюдаемого в ряде
изолированных галактик крупномасштабного искривления периферии их
дисков. Еще одна проблема, для решения которой необходимо изучение
динамики изгибных возмущений, связана с задачей объяснения
существенного различия толщин и ![]() -дисперсий скоростей объектов
звездного и газового дисков в плоских галактиках.
-дисперсий скоростей объектов
звездного и газового дисков в плоских галактиках.
Однако исследованные Хантером и Тоомре [501] модели холодных тонких дисков оказались устойчивыми относительно изгибных возмущений (подробное изложение теории этого вопроса см. в книге Фридмана и Поляченко [420]). В [362] было показано, что для решения упомянутых выше проблем необходимо изучать динамику изгибных возмущений в моделях дисков, горячих в их плоскости.
Очевидно, что такие локальные параметры, как ![]() -дисперсия
скоростей звезд и толщина диска, должны определяться из условия
устойчивости возмущений, масштабы которых малы по сравнению с его
толщиной. Соответствующее ВКБ-дисперсионное уравнение изгибных
возмущений в простейшей модели однородного тонкого невращающегося
звездного слоя можно записать в виде
[605]
-дисперсия
скоростей звезд и толщина диска, должны определяться из условия
устойчивости возмущений, масштабы которых малы по сравнению с его
толщиной. Соответствующее ВКБ-дисперсионное уравнение изгибных
возмущений в простейшей модели однородного тонкого невращающегося
звездного слоя можно записать в виде
[605]
Динамика крупномасштабных изгибных возмущений, охватывающих весь диск, должна, очевидно, изучаться с учетом вращения и структуры диска в целом. Такое исследование для ряда моделей тонких дисков [164] показало, что наиболее крупномасштабные моды могут быть неустойчивыми, если равновесие дисков в радиальном направлении обеспечивается в основном давлением, а не вращением. С уменьшением вклада давления в условие равновесия наиболее крупномасштабные моды стабилизируются, а более коротковолновые остаются неустойчивыми. Этот результат вместе с дисперсионным уравнением (2.132) показывает, что неустойчивость изгибных возмущений диска в некотором смысле является дополнительной к гравитационной неустойчивости возмущений в плоскости диска. Действительно, гравитация дестабилизирует возмущения в плоскости диска и стабилизирует изгибные; давление оказывается стабилизирующим фактором для возмущений в плоскости диска и дестабилизирующим для изгибных. Поэтому можно было бы ожидать, что самые крупномасштабные изгибные моды будут, в отличие от возмущений в плоскости диска (см. гл .3), дестабилизироваться достаточно массивной сфероидальной подсистемой. Обсуждению этого вопроса посвящен п. 2.5.3.
Определим, следуя Поляченко и Шухману
[172], максимальную анизотропию
![]() скоростей в звездном диске. Поскольку
вращение существенно только для возмущений, масштабы которых
сравнимы с радиусом диска, исходим из простой модели
бесстолкновительного невращающегося плоского слоя конечной толщины
[2], описываемой функцией распределения
скоростей в звездном диске. Поскольку
вращение существенно только для возмущений, масштабы которых
сравнимы с радиусом диска, исходим из простой модели
бесстолкновительного невращающегося плоского слоя конечной толщины
[2], описываемой функцией распределения
Считаем возмущения длинноволновыми в том смысле, что
характерный масштаб возмущения в плоскости слоя велик по
сравнению с его полутолщиной (![]() ). Однако
параметр
). Однако
параметр
![]() не
предполагаем малым. Ориентируем ось
не
предполагаем малым. Ориентируем ось ![]() вдоль направления
волнового вектора. Тогда зависимость
вдоль направления
волнового вектора. Тогда зависимость
![]() от
от
![]() в невращающемся слое становится несущественной и
задача сводится к двумерной.
в невращающемся слое становится несущественной и
задача сводится к двумерной.
Представим функцию распределения по ![]() в виде суперпозиции
потоков
в виде суперпозиции
потоков
Смещение границы слоя ![]() определяем из условия
определяем из условия
Для конкретных вычислений исходим из шварцшильдовской функции
распределения
![]() . В этом случае дисперсионное уравнение
(2.145) приводится к виду
. В этом случае дисперсионное уравнение
(2.145) приводится к виду
Данные наблюдений в околосолнечной окрестности Галактики
не противоречат оценке (2.149) -- согласно
[73, 190,
897] в среднем по не слишком молодым
звездам
![]() . Таким образом, в солнечной
окрестности Галактики звездный диск устойчив (согласно
(2.149)
-- с запасом) относительно изгибных возмущений промежуточных
масштабов
. Таким образом, в солнечной
окрестности Галактики звездный диск устойчив (согласно
(2.149)
-- с запасом) относительно изгибных возмущений промежуточных
масштабов
![]() (
(![]() - радиус диска
Галактики). То же самое можно, по-видимому, утверждать и в
отношении звездных дисков других плоских галактик
[317,
316,
559]. Обсуждение
результатов численных экспериментов можно найти в
§ 3.9.
Результаты вычисления
- радиус диска
Галактики). То же самое можно, по-видимому, утверждать и в
отношении звездных дисков других плоских галактик
[317,
316,
559]. Обсуждение
результатов численных экспериментов можно найти в
§ 3.9.
Результаты вычисления
![]() с учетом
вертикальной неоднородности диска получены S. Araki и обсуждаются в
[621].
с учетом
вертикальной неоднородности диска получены S. Araki и обсуждаются в
[621].
Для изучения динамики захватывающих весь диск плоской галактики крупномасштабных изгибных мод необходимо, очевидно, учитывать структуру диска и окружающей его сферической подсистемы в целом. Аналитическое решение такой задачи возможно только на достаточно простых моделях, и в этом разделе мы опишем первые результаты такого типа исследований [173].
Представим модель галактики в виде двухосного твердотельно
вращающегося звездного эллипсоида однородной плотности с полуосями
![]() ,
, ![]()
![]() , погруженного в протяженное однородное
сферическое гало. Равновесный гравитационный потенциал внутри
эллипсоида (модели диска)
, погруженного в протяженное однородное
сферическое гало. Равновесный гравитационный потенциал внутри
эллипсоида (модели диска)
а) ![]() (``купол'')
(``купол'')
Эти моды интересны прежде всего как наиболее крупномасштабные и
потому, как правило, самые опасные с точки зрения потери
устойчивости. Кроме того, следует ожидать, что поведение подобных
мод, захватывающих целиком всю систему, определяется небольшим
числом ее ``глобальных'' параметров. Это означает, что
исследование устойчивости рассматриваемой модели относительно
возбуждения перечисленных выше мод не потребует конкретизации
функции распределения -- достаточно лишь будет знать несколько
главных ее моментов. Для рассматриваемой модели однородного
эллипсоида выражения для линейных и квадратичных по скоростям
моментов определяются однозначно, если только предположить
изотропию в распределении скоростей в плоскости вращения.
Упомянутые моменты имеют вид
Метод исследования устойчивости стандартен
[2, 163,
420]. Сначала из уравнений
для лагранжевых смещений ![]() эти величины выражаются через
возмущенный потенциал
эти величины выражаются через
возмущенный потенциал ![]() . Затем вычисляются возмущения
плотности и нормальное смещение границы эллипсоида. Решая затем
уравнение Пуассона и сравнивая получившийся потенциал с исходным
(2.151)-(2.153), приходим к
системе линейных алгебраических уравнений относительно
коэффициентов, входящих в выражение для возмущенного потенциала.
Приравнивая, наконец, нулю определитель такой системы, получаем
искомое дисперсионное уравнение.
. Затем вычисляются возмущения
плотности и нормальное смещение границы эллипсоида. Решая затем
уравнение Пуассона и сравнивая получившийся потенциал с исходным
(2.151)-(2.153), приходим к
системе линейных алгебраических уравнений относительно
коэффициентов, входящих в выражение для возмущенного потенциала.
Приравнивая, наконец, нулю определитель такой системы, получаем
искомое дисперсионное уравнение.
=0.44 |
Дисперсионные уравнения для указанных выше мод
(2.151) ![]() (2.153) решались
численно (они довольно громоздки и здесь не приводятся).
Результаты их решения приведены на
рис. 2.9
(2.153) решались
численно (они довольно громоздки и здесь не приводятся).
Результаты их решения приведены на
рис. 2.9![]() а-в, соответствующих
различным значениям параметра
а-в, соответствующих
различным значениям параметра ![]() . Из этих рисунков
видно, что в дисковом пределе (
. Из этих рисунков
видно, что в дисковом пределе (
![]() ) каждая из
мод неустойчива при достаточно большой дисперсии скоростей звезд
(области под кривыми). С увеличением ``толщины'' эллипсоида
область неустойчивости по параметру
) каждая из
мод неустойчива при достаточно большой дисперсии скоростей звезд
(области под кривыми). С увеличением ``толщины'' эллипсоида
область неустойчивости по параметру ![]() сначала растет
(т.е. неустойчивыми становятся все более ``холодные'' системы), а
затем довольно быстро исчезает.
сначала растет
(т.е. неустойчивыми становятся все более ``холодные'' системы), а
затем довольно быстро исчезает.
Заметим, что резкий спад кривых -- границ областей неустойчивости
на рис. 2.9 происходит при такой сплюснутости
эллипсоида ![]() , для которой в используемой однородной модели
имеются резонансы между частотами колебаний звезд поперек
плоскости эллипсоида и в плоскости его вращения. Для мод
, для которой в используемой однородной модели
имеются резонансы между частотами колебаний звезд поперек
плоскости эллипсоида и в плоскости его вращения. Для мод ![]() и
и
![]() есть резонанс
есть резонанс
![]() , а для моды
, а для моды ![]() --
резонанс
--
резонанс
![]() . Столь сильное влияние этих
резонансов связано, очевидно, с идеализацией модели. Для реальных
дифференциально вращающихся систем эти кривые будут иметь более
гладкий вид.
. Столь сильное влияние этих
резонансов связано, очевидно, с идеализацией модели. Для реальных
дифференциально вращающихся систем эти кривые будут иметь более
гладкий вид.
Как видно из рис. 2.9, мода ![]() (``седло'')
сравнительно мало подвержена влиянию резонанса. Существенно,
однако, что именно эта мода обладает самой большой областью
неустойчивости по
(``седло'')
сравнительно мало подвержена влиянию резонанса. Существенно,
однако, что именно эта мода обладает самой большой областью
неустойчивости по ![]() при
при
![]() . Важно также
отметить, что с увеличением массы гало область неустойчивости по
параметру сплюснутости эллипсоида
. Важно также
отметить, что с увеличением массы гало область неустойчивости по
параметру сплюснутости эллипсоида ![]() сужается (неустойчивыми
остаются только сильно сплюснутые системы). Однако для моды
сужается (неустойчивыми
остаются только сильно сплюснутые системы). Однако для моды ![]() даже при очень больших значениях массы гало (
даже при очень больших значениях массы гало (
![]() )
эллипсоид неустойчив вплоть до
)
эллипсоид неустойчив вплоть до
![]() , то есть
значений, характерных для плоских подсистем спиральных галактик.
Тем самым можно говорить о выделенности седлообразной моды среди
других мод изгибного типа. Заметим, что аналогичное положение
имеет место и для возмущений, не изгибающих плоскость диска --
здесь тоже оказывается выделенной бароподобная мода
, то есть
значений, характерных для плоских подсистем спиральных галактик.
Тем самым можно говорить о выделенности седлообразной моды среди
других мод изгибного типа. Заметим, что аналогичное положение
имеет место и для возмущений, не изгибающих плоскость диска --
здесь тоже оказывается выделенной бароподобная мода ![]() .
.
В целом наиболее важным результатом является обнаружение
зависимости положения границ областей неустойчивости от массы
гало: при достаточно большой массе гало неустойчивыми могут стать
системы с малой дисперсией скоростей в плоскости эллипсоида [с
малым (
![]() )]. В этом и состоит дестабилизирующая
роль гало.
)]. В этом и состоит дестабилизирующая
роль гало.
В то же время с ростом массы гало необходимая для гравитационной
устойчивости диска дисперсия скоростей звезд в его плоскости
убывает:
![]() (см. гл. 3 и
рис. 3.20). Поэтому может оказаться, что
дестабилизирующая (по отношению к крупномасштабным изгибным
возмущениям) роль массивного гало не проявится. Исследуем этот
вопрос подробнее [56,
57,
627].
(см. гл. 3 и
рис. 3.20). Поэтому может оказаться, что
дестабилизирующая (по отношению к крупномасштабным изгибным
возмущениям) роль массивного гало не проявится. Исследуем этот
вопрос подробнее [56,
57,
627].
Предположим, что звездный диск обладает запасом гравитационной
устойчивости ![]() , который мы определим как отношение наблюдаемой
, который мы определим как отношение наблюдаемой
![]() к получаемой в численных экспериментах
к получаемой в численных экспериментах ![]() (полагаем,
что
(полагаем,
что ![]() соответствует границе гравитационной устойчивости).
Тогда везде за пределами центральной части диска
соответствует границе гравитационной устойчивости).
Тогда везде за пределами центральной части диска
=0.5 |
Результаты вычислений величины
![]() приведены на рис. 2.10 [заметим, что в
рамках рассматриваемой модели параметр
приведены на рис. 2.10 [заметим, что в
рамках рассматриваемой модели параметр
![]() (см.
рис. 2.9) выходит при
(см.
рис. 2.9) выходит при ![]() на
асимптотическое значение
на
асимптотическое значение
![]() ]. Видно, что
неустойчивыми оказываются только периферийные области систем с
малым
]. Видно, что
неустойчивыми оказываются только периферийные области систем с
малым ![]() . В системах же с
. В системах же с ![]() крупномасштабные изгибные
моды оказываются застабилизированными [области, близкие к
периферии эллипсоида (
крупномасштабные изгибные
моды оказываются застабилизированными [области, близкие к
периферии эллипсоида (
![]() ), не изучались, поскольку
в рамках рассматриваемой модели в противоречие с данными
наблюдений они слишком холодны: при
].
Таким образом, следует ожидать, что в галактиках с достаточно
массивным гало неустойчивость крупномасштабных изгибных мод не
будет проявляться.
=0.953
), не изучались, поскольку
в рамках рассматриваемой модели в противоречие с данными
наблюдений они слишком холодны: при
].
Таким образом, следует ожидать, что в галактиках с достаточно
массивным гало неустойчивость крупномасштабных изгибных мод не
будет проявляться.
=0.953
Рассмотрим некоторые особенности кинематики галактик, наблюдаемых с ребра (edge-on), с учетом влияния эффектов проекции, внутреннего поглощения и дисперсии скоростей газа или звезд на измеряемую кривую вращения галактик.
Для спиральных галактик, диски которых наблюдаются с ребра, вопрос о построении кривой вращения является нетривиальным из-за двух осложняющих факторов: эффекта проекции и эффекта внутреннего поглощения. Оба эффекта зависят как от формы кривой вращения, так и от распределения источников излучения и поглощающей среды в галактике. Отличительной особенностью кривых вращения, а точнее -- одномерных распределений лучевой скорости по диску, является протяженная область ``твердотельного'' вращения (монотонного роста скорости). Почти линейный рост лучевой скорости до больших расстояний от центра отмечался еще в первых работах по определению кинематики галактик с тонкими дисками [445]. Эти авторы, по-видимому, первыми обратили внимание на то, что твердотельная часть кривой вращения в галактиках, видимых с ребра, может являться артефактом, и что эффекты неоднородного распределения пыли требуют проведения огибающей линии, ограничивающей сверху положение точек на диаграмме ``радиус - измеренная скорость вращения''.
Позднее проведенное сравнение формы кривой вращения во внутренней области галактик со степенью наклона диска к лучу зрения показало, что градиент измеряемой скорости вращения во внутренней области галактики действительно ниже у сильно наклоненных дисков, и этот эффект сильнее проявляется для галактик высокой светимости, обладающих в среднем более сильным внутреннем поглощением [444].
|
=0.998 |
Более 300 кривых вращения для галактик, наблюдаемых с
ребра (из каталога плоских галактик FGC
[531]),
было получено на 6-м телескопе САО РАН (см.
[599] и
ссылки в этой работе).
Результаты измерений подтвердили, что подавляющее
большинство этих галактик имеют очень протяженный
``твердотельный'' участок, иногда простирающийся до внешней
границы измеряемой кривой, хотя имеются и исключения
[104,
105,
106].
Как пример, на рис. 2.11![]() a
показано несколько достаточно
типичных кривых вращения для галактик по работе
[105].
Рисунки 2.11
a
показано несколько достаточно
типичных кривых вращения для галактик по работе
[105].
Рисунки 2.11![]() б,
б,![]() в
иллюстрируют более редко встречающиеся особенности
кривых, которые обсуждаются ниже
(в п. 2.6.4).
В связи с интерпретацией кривых вращения возникает
вопрос -- как влияют различные эффекты на
измеряемые скорости вращения таких галактик, и можно
ли непосредственно из наблюдений получить
действительную кривую вращения галактики и оценку
максимальной скорости вращения дисков?
Для осесимметричных моделей галактик с заданными кривыми вращения
рассчитаем распределения лучевой скорости
в
иллюстрируют более редко встречающиеся особенности
кривых, которые обсуждаются ниже
(в п. 2.6.4).
В связи с интерпретацией кривых вращения возникает
вопрос -- как влияют различные эффекты на
измеряемые скорости вращения таких галактик, и можно
ли непосредственно из наблюдений получить
действительную кривую вращения галактики и оценку
максимальной скорости вращения дисков?
Для осесимметричных моделей галактик с заданными кривыми вращения
рассчитаем распределения лучевой скорости ![]() вдоль большой
оси диска, видимого с ребра, следуя
[64].
вдоль большой
оси диска, видимого с ребра, следуя
[64].
Случай с малым внутренним поглощением может реально относиться к
измерениям скорости вращения в радиодиапазоне, либо в галактиках с
очень низким содержанием межзвездной среды, либо же к измерениям
скоростей внешней зоны с низкой оптической толщиной ![]() .
.
При отсутствии внутреннего поглощения максимальные значения допплеровского компонента скорости вращения относятся к областям, находящимся на диаметре галактики, перпендикулярном лучу зрения (условно будем называть его большой осью галактики). Поэтому оценки максимальной скорости источников на данном расстоянии от центра должны представлять собой (с точностью до значения дисперсии скоростей) действительную скорость кругового вращения. Однако это значение скорости в общем случае не обязательно будет соответствовать центру тяжести (барицентру) профиля линии, поскольку его положение зависит от распределения не только скорости, но и объемной светимости вдоль луча зрения.
|
=0.999 |
Будем считать, что скорость вращения диска, как и его
яркость в спектральной линии, используемой для
измерения скоростей, распределены осесимметрично.
Обозначим объемную светимость в линии через ![]() .
Пусть ось
.
Пусть ось ![]() соответствует большой оси галактики, а
ось
соответствует большой оси галактики, а
ось ![]() направлена вдоль луча зрения
(рис. 2.12
направлена вдоль луча зрения
(рис. 2.12![]() а).
Тогда средняя скорость, взвешенная по удельной светимости
вдоль луча зрения, определяется выражением
а).
Тогда средняя скорость, взвешенная по удельной светимости
вдоль луча зрения, определяется выражением
Запишем также формулы для наблюдаемой вдоль луча зрения
дисперсии скоростей.
При больших значениях угла наклона галактики ![]() (
(
![]() )
помимо эффекта, связанного с интегрированием вдоль
луча зрения, что дает:
)
помимо эффекта, связанного с интегрированием вдоль
луча зрения, что дает:
Рассмотрим, как действительная форма кривой вращения
![]() и особенности распределения вещества в
диске влияют на зависимость
и особенности распределения вещества в
диске влияют на зависимость ![]() (наблюдаемую
кривую вращения).
(наблюдаемую
кривую вращения).
Пусть объемная светимость диска в линии ![]() , по которой
оценивается скорость, уменьшается с
, по которой
оценивается скорость, уменьшается с ![]() по экспоненциальному
закону
по экспоненциальному
закону
![]() , где
, где ![]() -- радиальная шкала
изменения яркости диска в эмиссионной линии, а в случае
определения скоростей по абсорбционным линиям
-- радиальная шкала звездного диска.
Примем для определенности
-- радиальная шкала
изменения яркости диска в эмиссионной линии, а в случае
определения скоростей по абсорбционным линиям
-- радиальная шкала звездного диска.
Примем для определенности ![]() .
На расстояниях
.
На расстояниях ![]() вклад диска в
наблюдаемый профиль линии будем считать равным нулю.
Для иллюстрации ограничимся рассмотрением трех типов
кривых вращения, формы которых различаются во внутренней области
диска (
вклад диска в
наблюдаемый профиль линии будем считать равным нулю.
Для иллюстрации ограничимся рассмотрением трех типов
кривых вращения, формы которых различаются во внутренней области
диска (![]() ) (рис. 2.12
) (рис. 2.12![]() б):
б):
1) Кривая вращения
![]() ,
характерная для галактик без массивного балджа
(точечная линия на
рис. 2.12
,
характерная для галактик без массивного балджа
(точечная линия на
рис. 2.12![]() б).
б).
2) Кривая второго типа
![]() ,
реализующаяся в случае маломассивного балджа,
ответственного за более крутой градиент скорости во
внутренней области галактики (штриховая линия на
рис. 2.12
,
реализующаяся в случае маломассивного балджа,
ответственного за более крутой градиент скорости во
внутренней области галактики (штриховая линия на
рис. 2.12![]() б).
Область ``твердотельного'' вращения мала.
б).
Область ``твердотельного'' вращения мала.
3) Кривая
![]() с околоядерным максимумом
скорости вращения (сплошная линия на
рис. 2.12
с околоядерным максимумом
скорости вращения (сплошная линия на
рис. 2.12![]() б), который отражает
существование массивного концентрированного балджа.
б), который отражает
существование массивного концентрированного балджа.
Во всех случаях кривая вращения выходит на плато на больших ![]() .
На рис. 2.12
.
На рис. 2.12![]() в изображены радиальные
зависимости скорости диска вдоль луча зрения
в изображены радиальные
зависимости скорости диска вдоль луча зрения ![]() , вычисленные
по формуле (2.158), для трех рассматриваемых типов
кривых вращения при отсутствии поглощения.
Как видим, во всех случаях во всем диске наблюдается
значительная недооценка скорости вращения, особенно в
центральной области.
При этом различие между 2-м и 3-м типами кривых
практически исчезает, а недооценка скорости вращения
оказывается наибольшей для кривой вращения
, вычисленные
по формуле (2.158), для трех рассматриваемых типов
кривых вращения при отсутствии поглощения.
Как видим, во всех случаях во всем диске наблюдается
значительная недооценка скорости вращения, особенно в
центральной области.
При этом различие между 2-м и 3-м типами кривых
практически исчезает, а недооценка скорости вращения
оказывается наибольшей для кривой вращения
![]() .
Только на самом краю диска имеет место примерное
равенство
.
Только на самом краю диска имеет место примерное
равенство
![]() .
Поскольку кривые изменения скорости
.
Поскольку кривые изменения скорости ![]() очень слабо зависят
от реальной формы кривой вращения
очень слабо зависят
от реальной формы кривой вращения ![]() , они не позволяют
восстановить распределение массы в галактике
[64].
, они не позволяют
восстановить распределение массы в галактике
[64].
=1.05
При прохождении излучения сквозь вещество диска вклад
от более далеких областей галактики оказывается
меньшим, чем от расположенных ближе к наблюдателю.
Для света, распространяющегося в диске под малым
углом к его плоскости, галактики, содержащие пыль,
практически непрозрачны.
Поэтому можно считать, что от наиболее удаленной зоны
излучение не доходит до наблюдателя.
Излучение средней области, на которую приходятся
максимальные значения проекции скорости вращения на луч зрения,
существенно ослаблено, причем чем ближе к центру системы, тем
сильнее влияние поглощения.
В результате в центральной области галактики
![]() основной вклад в излучение дает ближайшая
зона, в которой скорость вдоль луча зрения
невелика.
С учетом поглощения выражение (2.158)
принимает вид:
основной вклад в излучение дает ближайшая
зона, в которой скорость вдоль луча зрения
невелика.
С учетом поглощения выражение (2.158)
принимает вид:
Ограничимся осесимметричным экспоненциальным распределением пыли
=0.999 |
На рис. 2.13 показаны результаты расчетов по
формуле (2.161) с учетом
(2.162), (2.163) для
радиальных шкал распределения яркости эмиссии и плотности пыли
![]() кпк и
кпк и ![]() кпк соответственно, при различных значениях
параметра
кпк соответственно, при различных значениях
параметра ![]() .
Во всех случаях поглощение сильно уменьшает скорость
.
Во всех случаях поглощение сильно уменьшает скорость
![]() -- за исключением внешней, относительно
прозрачной, области галактики.
Вследствие этого происходит ``спрямление''
наблюдаемой кривой вращения, так что в сильно
запыленном диске практически линейный рост
-- за исключением внешней, относительно
прозрачной, области галактики.
Вследствие этого происходит ``спрямление''
наблюдаемой кривой вращения, так что в сильно
запыленном диске практически линейный рост ![]() может прослеживаться вплоть до внешней границы диска
независимо от реальной формы кривой вращения
(см. рис. 2.13).
Наличие ``кольца'' и центральной ``дыры''
в распределении газа еще более усиливают указанную
особенность хода кривой
может прослеживаться вплоть до внешней границы диска
независимо от реальной формы кривой вращения
(см. рис. 2.13).
Наличие ``кольца'' и центральной ``дыры''
в распределении газа еще более усиливают указанную
особенность хода кривой ![]() в моделях с поглощением
[64].
в моделях с поглощением
[64].
В рассмотренных выше моделях считалось, что дисперсия
скоростей источников излучения равна нулю, имеется
только регулярное вращение.
Учтем теперь остаточные скорости, которые будем
характеризовать значениями дисперсии радиальных ![]() и
азимутальных
и
азимутальных ![]() скоростей.
Если кривая вращения оценивается по звездным спектрам,
то в соответствии с наблюдениями (см., например,
[321]) можно
считать, что как
скоростей.
Если кривая вращения оценивается по звездным спектрам,
то в соответствии с наблюдениями (см., например,
[321]) можно
считать, что как ![]() , так и
, так и ![]() уменьшаются
с удалением от центра.
Для
уменьшаются
с удалением от центра.
Для ![]() примем простое выражение
примем простое выражение
![]() .
Радиальная шкала дисперсии скоростей
.
Радиальная шкала дисперсии скоростей ![]() , как
правило, существенно превышает шкалу изменения
плотности
, как
правило, существенно превышает шкалу изменения
плотности ![]() [111].
Функцию распределения по скоростям выберем в виде (см.
(3.16))
[111].
Функцию распределения по скоростям выберем в виде (см.
(3.16))
=0.998 |
Рассмотрим отдельно влияние описанных выше факторов на наблюдаемые
кривые вращения динамически горячей (звездный диск) и холодной
(газовый диск) подсистем для галактик, наблюдаемых с ребра.
Для газового диска
![]() (
(![]() -- максимальная скорость вращения), и распределение
скоростей является изотропным (
-- максимальная скорость вращения), и распределение
скоростей является изотропным (
![]() ).
На рис. 2.14 показаны профили
скорости (допплеровские профили линии)
).
На рис. 2.14 показаны профили
скорости (допплеровские профили линии)
![]() на различных расстояниях
на различных расстояниях ![]() от центра диска.
В отсутствии пыли (рис. 2.14
от центра диска.
В отсутствии пыли (рис. 2.14![]() а)
профили сильно различаются для различных значений
а)
профили сильно различаются для различных значений
![]() .
При этом характерной особенностью профилей
является их асимметрия, а для центральной области (кривые
1-3 на рис. 2.14
.
При этом характерной особенностью профилей
является их асимметрия, а для центральной области (кривые
1-3 на рис. 2.14![]() а) -- наличие двух
максимумов или длинного крыла со ``ступенькой'' вместо второго
максимума (кривые 4-7).
Первый максимум (на больших скоростях)
обусловлен быстрым вращением вещества в области
вблизи ``большой оси'' (см.
рис. 2.12
а) -- наличие двух
максимумов или длинного крыла со ``ступенькой'' вместо второго
максимума (кривые 4-7).
Первый максимум (на больших скоростях)
обусловлен быстрым вращением вещества в области
вблизи ``большой оси'' (см.
рис. 2.12![]() а).
Второй максимум или ``ступенька'' (в области меньших скоростей) связаны
с двумя факторами: с наличием остаточных скоростей, но в большей
степени с сильным уменьшением проекции
а).
Второй максимум или ``ступенька'' (в области меньших скоростей) связаны
с двумя факторами: с наличием остаточных скоростей, но в большей
степени с сильным уменьшением проекции ![]() на луч
зрения при
на луч
зрения при
![]() .
.
В сильнозапыленном диске ситуация качественно меняется
(рисунок 2.14![]() б).
Все профили
б).
Все профили ![]() в центральной области обладают только одним максимумом
(из двух максимумов, имевших место в предыдущем случае,
остается лишь соответствующий более низкой скорости).
Максимум на более высокой скорости возникает лишь в том случае,
когда поглощение достаточно мало, чтобы позволить наблюдать области вблизи большой оси
на данном расстоянии
в центральной области обладают только одним максимумом
(из двух максимумов, имевших место в предыдущем случае,
остается лишь соответствующий более низкой скорости).
Максимум на более высокой скорости возникает лишь в том случае,
когда поглощение достаточно мало, чтобы позволить наблюдать области вблизи большой оси
на данном расстоянии ![]() .
.
Для звездного диска дисперсия скоростей выше, чем
для газа.
Для осесимметричной модели справедливо соотношение
(2.34).
В случае звездного диска с дисперсией радиальных скоростей
звезд в центре
![]() распределения
распределения ![]() (где
(где
![]() берется по модулю, поскольку речь идет об абсорбционных
линиях) приведены на рис. 2.14
берется по модулю, поскольку речь идет об абсорбционных
линиях) приведены на рис. 2.14![]() в,г.
И в этом случае, как и в случае эмиссионного газа, при наличии поглощения
максимальные значения
в,г.
И в этом случае, как и в случае эмиссионного газа, при наличии поглощения
максимальные значения ![]() смещаются в область меньших скоростей.
смещаются в область меньших скоростей.
=0.48 |
Сложная форма профилей линии приводит к различию в
оценках лучевой скорости по измерению длин волн,
соответствующих максимуму интенсивности, и длин волн
барицентра линии.
На рис. 2.15 показаны
зависимости ![]() и
и ![]() , построенные
по положению максимумов у профилей
, построенные
по положению максимумов у профилей ![]() ,
приведенных на рис. 2.14.
В соответствии со
сказанным выше, при наличии двух максимумов выбирался тот, который
связан с более высокой скоростью. В модели для газового диска без
поглощения (рис. 2.14
,
приведенных на рис. 2.14.
В соответствии со
сказанным выше, при наличии двух максимумов выбирался тот, который
связан с более высокой скоростью. В модели для газового диска без
поглощения (рис. 2.14![]() а) при таком способе
оценки скорости различие между реальной скоростью вращения
а) при таком способе
оценки скорости различие между реальной скоростью вращения
![]() и
и ![]() (кривая 1 и 2 на
рис. 2.15)) оказывается малой, и для
рассматриваемого случая не превышает 7 % (см.
рис. 2.15).
(кривая 1 и 2 на
рис. 2.15)) оказывается малой, и для
рассматриваемого случая не превышает 7 % (см.
рис. 2.15).
Для звездного населения с большой дисперсией
скоростей
![]() разность
разность
![]() существенно выше, однако и в
этом случае наличие внутреннего максимума на кривой
вращения хорошо прослеживается (кривая 3),
хотя его амплитуда заметно меньше.
существенно выше, однако и в
этом случае наличие внутреннего максимума на кривой
вращения хорошо прослеживается (кривая 3),
хотя его амплитуда заметно меньше.
=1
Таким образом, подход, основанный на определении
максимума ![]() , дает более правильный результат при
построении кривой вращения, чем рассмотренный в
п.
, дает более правильный результат при
построении кривой вращения, чем рассмотренный в
п. ![]() 2.6.3 способ
средневзвешенного значения лучевой скорости, определяемой по
барицентру спектральной линии.
К сожалению, в реальных галактиках профили линии
могут быть искажены неоднородным распределением
эмиссионных областей и поглощающей среды.
Однако асимметрия профиля, если таковая присутствует,
вполне может быть измерена и принята во внимание при
оценке скорости.
2.6.3 способ
средневзвешенного значения лучевой скорости, определяемой по
барицентру спектральной линии.
К сожалению, в реальных галактиках профили линии
могут быть искажены неоднородным распределением
эмиссионных областей и поглощающей среды.
Однако асимметрия профиля, если таковая присутствует,
вполне может быть измерена и принята во внимание при
оценке скорости.
В сильно запыленном диске и для газового и для
звездного населения зависимости ![]() , найденные
двумя методами, мало различаются (кривые 4 и
5 на рис. 2.15).
В обоих случаях получаемая кривая
, найденные
двумя методами, мало различаются (кривые 4 и
5 на рис. 2.15).
В обоих случаях получаемая кривая ![]() не дает
правильного представления о форме действительной
кривой вращения во внутренней области диска.
не дает
правильного представления о форме действительной
кривой вращения во внутренней области диска.
Наиболее интересен промежуточный случай, когда в
центральной области галактики поглощение сильно
(профиль линии имеет только один максимум
-- на малых скоростях), а, начиная с некоторого значения ![]() ,
существенный вклад в излучение дают области вблизи большой оси,
ответственные за появление максимума с высоким значением лучевой скорости.
В этом случае кривая вращения, построенная по положению максимумов
в профилях линии, обнаруживает резкий ``скачок'' -- от скоростей,
существенно меньших скорости вращения, к скоростям,
близким к последней (кривая 6 на рис. 2.15).
Чем меньше поглощение в
галактике, тем ближе к центру осуществляется этот переход.
Варьируя значения
,
существенный вклад в излучение дают области вблизи большой оси,
ответственные за появление максимума с высоким значением лучевой скорости.
В этом случае кривая вращения, построенная по положению максимумов
в профилях линии, обнаруживает резкий ``скачок'' -- от скоростей,
существенно меньших скорости вращения, к скоростям,
близким к последней (кривая 6 на рис. 2.15).
Чем меньше поглощение в
галактике, тем ближе к центру осуществляется этот переход.
Варьируя значения ![]() , можно получить,
что подъем измеряемой скорости вращения происходит на
таком радиусе
, можно получить,
что подъем измеряемой скорости вращения происходит на
таком радиусе ![]() , на котором поглощение падает ниже
, на котором поглощение падает ниже
![]() зв. величины
на кпк. Заметим, что подобная ступенька на кривой вращения
действительно наблюдается у ряда галактик, видимых с ребра (см.
пример на
рис. 2.11
зв. величины
на кпк. Заметим, что подобная ступенька на кривой вращения
действительно наблюдается у ряда галактик, видимых с ребра (см.
пример на
рис. 2.11![]() б).
б).
Заметим, что в некоторых галактиках, наблюдаемых с ребра, кривые
изменения лучевых скоростей ![]() , в отличие от ожидаемого,
не демонстрируют твердотельного вращения. В этих галактиках
центральная область отличается высоким градиентом лучевой скорости
(см. рис. 2.11
, в отличие от ожидаемого,
не демонстрируют твердотельного вращения. В этих галактиках
центральная область отличается высоким градиентом лучевой скорости
(см. рис. 2.11![]() в).
Такое поведение указывает либо на очень низкое содержание
пыли в галактике, либо (что более вероятно) на существенное отличие угла
наклона диска от
в).
Такое поведение указывает либо на очень низкое содержание
пыли в галактике, либо (что более вероятно) на существенное отличие угла
наклона диска от ![]() . Отличия на несколько градусов может быть достаточно,
чтобы эффекты проекции и внутреннего поглощения стали несущественными (точная оценка угла, при котором это имеет место, зависит от толщины диска и пространственного распределения как источников, так и поглощающей среды).
Отметим, что влияние эффекта проекции зависит не только от угла
наклона диска
. Отличия на несколько градусов может быть достаточно,
чтобы эффекты проекции и внутреннего поглощения стали несущественными (точная оценка угла, при котором это имеет место, зависит от толщины диска и пространственного распределения как источников, так и поглощающей среды).
Отметим, что влияние эффекта проекции зависит не только от угла
наклона диска ![]() , но и от ширины щели спектрографа. Так, если
щель ориентирована вдоль большой оси галактики и ее ширина
сопоставима с видимой толщиной диска (точнее - с размером малой
оси эллипса, который ограничивает измеряемую область диска), то
диск будет восприниматься как наблюдаемый с ребра, даже если угол
его наклона отличается от
, но и от ширины щели спектрографа. Так, если
щель ориентирована вдоль большой оси галактики и ее ширина
сопоставима с видимой толщиной диска (точнее - с размером малой
оси эллипса, который ограничивает измеряемую область диска), то
диск будет восприниматься как наблюдаемый с ребра, даже если угол
его наклона отличается от ![]() .
.
Расчеты, описанные здесь, относятся к кривой вращения
![]() (см. рис. 2.12
(см. рис. 2.12![]() б).
Для случаев
б).
Для случаев
![]() или
или
![]() основные
выводы сохраняют свою силу.
основные
выводы сохраняют свою силу.
Как показывают наблюдения,
распределение пыли по диску галактик часто носит сильно
несимметричный и неоднородный характер на мелких масштабах ().
Для иллюстрации рассмотрим модель, в которой поглощающие области распределены ``пятнами'', раскиданными случайным образом по диску.
Концентрация пыли в ![]() -м облаке (
-м облаке (
![]() ) с
координатами центра
) с
координатами центра
![]() будем характеризовать
величиной
будем характеризовать
величиной
![]() ,
которая подчиняется закону (2.163).
Размеры облаков
,
которая подчиняется закону (2.163).
Размеры облаков ![]() в рассматриваемой модели задавались случайно из интервала
в рассматриваемой модели задавались случайно из интервала
![]() .
.
|
=0.49 |
На рис. 2.16 показана радиальная
зависимость скорости ![]() в модели с
в модели с ![]() ,
(кривые 3 и 4). Очевидно, что разброс точек или
неровная форма кривой
,
(кривые 3 и 4). Очевидно, что разброс точек или
неровная форма кривой ![]() , несимметричной относительно центра
галактики, является результатом существования случайно
расположенных коридоров прозрачности, позволяющих на некоторых
направлениях наблюдать области в глубине диска.
Амплитуда вариации скорости может быть
значительной, и для получения кривой вращения следует
провести верхнюю огибающую точек на диаграмме
, несимметричной относительно центра
галактики, является результатом существования случайно
расположенных коридоров прозрачности, позволяющих на некоторых
направлениях наблюдать области в глубине диска.
Амплитуда вариации скорости может быть
значительной, и для получения кривой вращения следует
провести верхнюю огибающую точек на диаграмме
![]() , но и в этом случае форма кривой может быть
прослежена лишь приблизительно
[445].
Если средняя
плотность пыли достаточно мала, так что мы наблюдаем на различных
расстояниях
, но и в этом случае форма кривой может быть
прослежена лишь приблизительно
[445].
Если средняя
плотность пыли достаточно мала, так что мы наблюдаем на различных
расстояниях ![]() области, лежащие вблизи большой оси, то такая
процедура действительно дает возможность получить кривую вращения.
Однако это скорее относится к внешним областям галактики, где
области, лежащие вблизи большой оси, то такая
процедура действительно дает возможность получить кривую вращения.
Однако это скорее относится к внешним областям галактики, где
![]() мало. В рассматриваемой модели даже огибающая точек на
диаграмме
мало. В рассматриваемой модели даже огибающая точек на
диаграмме ![]() (штриховая линия на
рис. 2.16) оказывается далекой от
заданной формы кривой вращения.
(штриховая линия на
рис. 2.16) оказывается далекой от
заданной формы кривой вращения.
Другой эффект, создаваемый неоднородностью в распределении пыли,
естественно ожидать для галактик с развитой спиральной структурой.
Определенная ориентация спиральных ветвей, к которым
концентрируется межзвездная среда, приводит к различной
прозрачности диска по разные стороны от центра. Там, где
спиральная ветвь находится на стороне галактики, обращенной к
наблюдателю, луч зрения проникает в диск на меньшую глубину, что
уменьшает оценку скорости вращения. Это приводит к тому, что
измеряемые кривые ![]() оказываются несимметричными
относительно центра. Подобные случаи действительно наблюдаются
(см. рис. 2.11
оказываются несимметричными
относительно центра. Подобные случаи действительно наблюдаются
(см. рис. 2.11![]() в).
Более близкой к действительной форме кривой вращения следует
считать кривую, проведенную по более высоким значениям измеренных
скоростей [64].
в).
Более близкой к действительной форме кривой вращения следует
считать кривую, проведенную по более высоким значениям измеренных
скоростей [64].
Заметим, что все наблюдаемые кривые вращения (зависимости
![]() на больших
на больших ![]() выходят на ``плато'', соответствующее
заданной скорости вращения модельной галактики. Следовательно,
измеряемые максимальные скорости вращения дисков, наблюдаемых с
ребра, должны мало отличаться от действительных.
выходят на ``плато'', соответствующее
заданной скорости вращения модельной галактики. Следовательно,
измеряемые максимальные скорости вращения дисков, наблюдаемых с
ребра, должны мало отличаться от действительных.