<< 2. Динамика звездного диска 4. Аккpеционные диски >>

Subsections

• 3.1 Динамические модели
• 3.2 Кpупномасштабная стpуктуpа звездных дисков
• 3.3 Звездные диски на границе гравитационной устойчивости
• 3.4 Оценка массы сфероидальных подсистем
  для выборки дисковых галактик
• 3.5 Изгибные неустойчивости звездного диска
• 3.6 Ограничения на параметры Галактики (Milky Way)
• 3.7 Асимметричные галактики (lopsided-галактики)
• 3.8 Сложные несимметричные структуры в центре галактик
• 3.9 Релаксационные пpоцессы в звездном диске
• 3.10 Пpиливные эффекты

3. Численное моделиpование звездных дисков

3.1 Динамические модели

Методов прямого лабораторного моделирования коллективных процессов в непрерывной или дискретной гравитирующей среде пока не существует. Вряд ли они будут разработаны и в обозримом будущем. Но появление достаточно мощных ЭВМ открыло уникальную возможность численного моделирования таких явлений и тем самым создало своеобразную экспериментальную базу для физики коллективных процессов в гравитирующих системах. В приложении к плоским галактикам такое моделирование может иметь целью определение темпа коллективных релаксационных процессов и направления эволюционных изменений тех или иных параметров диска, выяснение пространственной структуры квазистационарных плоских галактик и отдельных их подсистем, а также изучение тех процессов, которые могли бы привести к образованию таких наблюдаемых структур, как спиральные узоры, бары, особенности во взаимодействующих галактиках и т. п.

Figure: Число публикаций по физике галактик и космологии, в которых полученные результаты в существенной мере основаны на моделях $N\!$-тел. Пунктирная линия соответствует закону $\propto\exp(t/7~\textrm{лет})$

=0.5

Практически устоявшимся термином для обозначения численного моделирования гравитирующих $N\!$-тел (как, впрочем, и газодинамических систем) стало словосочетание ``численный (или компьютерный) эксперимент''. Численный эксперимент в последние годы становится одним из основных инструментов в руках теоретиков при изучении динамики звездных систем. Наблюдается буквально золотая лихорадка, характеризующаяся экспоненциальным ростом числа публикаций (рис. 3.1). В то же время, поскольку число нерешенных еще задач существенно больше рассмотренных, то в основе полученных результатов лежит обычно небольшая серия расчетов одной группы исследователей. Как представляется, имеется насущная необходимость повторения полученных ранее результатов, чтобы с большим доверием к ним относиться, как это и принято в экспериментальной физике.

В следующем пункте рассмотрим основные численные методы вычисления гравитационной силы (или потенциала) от заданного распределения массы.

3.1.1 Модели $N\!$-тел

1) В основе прямого метода ($PP$ = ``частица-частица'') лежит учет гравитационного взаимодействия всех частиц друг с другом [203, 685]. Такой метод представляется наиболее простым для понимания и реализации и, самое главное, обеспечивает при прочих равных условиях наилучшую точность вычисления гравитационной силы, однако он требует и наибольших машинных ресурсов, поскольку каждая частица взаимодействует с каждой. Поэтому такой подход можно использовать в качестве ``модели-теста'', проверяя с его помощью наиболее важные принципиальные результаты.

В моделях такого типа число частиц, как правило, не превышает значений ^3.1 $N \,\lee\, 10^4$. Число арифметических действий, необходимых для интегрирования одного временного шага в рамках модели PP, равно $10 \cdot N^2 - N$. Нетрудно оценить, что при использовании ЭВМ, для которой необходима 1 мкс на выполнение одной операции, при $N = 10^3$ на один временной шаг (а всего их требуется, как правило, несколько тысяч) затрачивается 10 с, а при $N = 10^5$ больше суток!

Преимущество модели этого типа связано с возможностью определять силы с такой же точностью, что и арифметическая точность ЭВМ, и именно в экспериментах с такими моделями получен ряд важных результатов [108, 129, 130, 207, 226, 681, 685, 879, 880 и др.].

2) Группа методов под условным названием ``частицы в сетке'' ($\!PM$ = Particle-Mesh), включая различные модификации (Cloud-in-Cell, Triangular-Shaped-Cloud, $P^3M$). Для них характерно использование быстрого Фурье-преобразования для решения уравнения Пуассона. Алгоритмы различаются способами вычисления сил от ближних и дальних частиц [11, 203, 629].

Конфигурационное пространство и, в ряде случаев, пространство скоростей разбиваются на ячейки, в которых и локализуются частицы. Непосредственно в модели PM взаимодействие частиц, находящихся внутри одной и той же ячейки, не учитывается, а взаимодействие частиц, находящихся в различных ячейках, моделируется ньютоновскими гравитационными силами, вычисляемыми, как правило, по координатам центров ячеек. Тем самым осуществляется полное ``выключение'' гравитационного взаимодействия на расстояниях, меньших размера ячейки (масштаб ``обрезания'' потенциала равен размеру ячейки). Поскольку число ячеек $N_M$ много меньше $N$, получается выигрыш в скорости расчета. Модели этого типа подробно описаны в работах [301, 486, 487, 488, 629, 630, 632, 722] и в ряде других.

Учет взаимодействия между центрами пространственных ячеек при большом числе частиц в каждой ячейке обычно осуществляется с использованием дискретного аналога теоремы о свертке и алгоритма быстрого преобразования Фурье.

Предложены модели (``частица-частица-частица-сетка''=$\!P^3M\!$), которые отчасти соединяют быстроту расчета метода и учет близкодействующих сил, как в моделях $\!PP\!\!$. В их основе лежит расщепление действующих между частицами сил на быстро меняющуюся короткодействующую часть и медленно меняющуюся дальнодействующую.

3) Предложен ряд схем ($PM^2$ = Particle-Multiple-Mesh [436], NGPM = Nested-Grid Particle-Mesh [831]), в которых используют несколько сеток с разным шагом, причем структура сеток динамически меняется со временем с учетом перераспределения вещества в расчетной области [620]. Такой подход позволяет получать выигрыш в количестве операций. Сюда можно отнести и иерархические схемы, в частности, различные версии TREEcode, например, TREEcode (Top Down) [275, 276] с учетом усовершенствований [641].

Система сеток располагается в порядке подробности от наиболее мелких, где учитываются наиболее близкодействующие силы, которые учитываются достаточно точно, ко все более крупномасштабным, на которых учитываются дальнодействующие силы. Другими словами, производится регуляризация подсистем на разных уровнях иерархии. Алгоритм требует порядка $N\cdot\ln N$ вычислений на каждом временном шаге интегрирования.

TREEcode (Bottom Up) отличается от TREEcode (Top Down) направлением прохода граф-дерева от ближайших частиц ко все более укрупненным блокам [518, 641]. Такой подход позволяет вести расчет с разным временным шагом $\littlDelta t$ для различных частиц. Выбирая для частиц, которые находятся в области больших градиентов полей, меньшие значения $\littlDelta t$ (но кратные максимальному значению $\littlDelta t^{max}$), удается повысить точность вычислений. Алгоритм TREEcode (Bottom Up) наиболее эффективен при моделировании систем, где роль парных сближений (включая тесные двойные звезды) является важной. Данный алгоритм является более сложным для реализации, но он дает возможность изучать столкновительные системы типа шаровых скоплений.

Figure: Зависимость времени вычисления одного шага интегрирования $\tau$ (условные единицы) от параметра $\Theta$ при прочих равных условиях

=0.45

Фактически, единственным свободным параметром, определяющим точность вычисления сил в методе TREEcode, является угол раствора $\Theta$. C уменьшение $\Theta$ точность увеличивается, однако время вычисления одного шага интегрирования по времени нелинейно зависит от значения $\Theta$ (рис. 3.2). Проведенный нами анализ подтверждает вывод [477], что при изучении галактик приемлемым выбором является $\Theta\lee 0,\!6\div 1$. При моделировании крупномасштабных структур можно принять $\Theta=1$, в случае рассмотрения сильно неоднородных на малых масштабах распределений необходимо задавать $\Theta=0,\!5\!$.

Достаточно детальное описание метода с некоторыми модификациями дано в работе [518]. Сравнение с известными модельными результатами показало хорошее соответствие, а также подтвердило преимущества, связанные с затратами машинного времени. TREE-модели позволяют изучать сложные системы, включающие три взаимодействующие компоненты: звездный и газовый диски, ``живое'' гало [470, 798]. Введение в практику иерархических схем фактически подводит нас к естественному пределу в построении численных методов [480]. В последние годы развитие пошло по пути создания специализированных компьютеров для численного решения гравитационной задачи $N\!$-тел (например, GRAPE), в которых вычисление взаимодействия между телами реализовано аппаратно [533, 839]. Непосредственное моделирование на такого рода компьютерах говорит об их больших возможностях [600].

Сравнительный обзор различныых методов численного моделирования $N$ гравитирующих тел можно найти, например, в [203, 451, 778].

Дальнейшим развитием TREEcode можно считать $FMM$ (=Fast Multipole Method) алгоритмы, в которых используются разные мультипольные разложения поля для далеких и близких областей [451, 641]. Потенциал в заданной точке берется в виде ряда мультипольного разложения, что более экономно по сравнению с вычислением силы с заданной точностью. Увеличивая число членов в разложении, можно получать сколь-угодно точные решения в ущерб, разумеется, времени вычислений.

Предложены алгоритмы, объединяющие TREEcode и $PM\!$-схемы [376], что позволяет уменьшить время расчета за счет точности, однако эти методы недостаточно апробированы.

Одной из важнейших проблем моделей $N\!$-тел в приложении к динамике галактик является влияние шума из-за малости числа частиц по сравнению c числом звезд. Стандартным способом уменьшения шума и обеспечение бесстолкновительности является ``обрезание'' Ньютоновского потенциала на малых расстояниях [368, 742, 743]. Для снижения роли шума начинают развиваться специальные методы Wavelets, позволяющие существенно ослабить этот эффект [744].

При моделировании полной галактики, состоящей из $N_* \simeq 10^{10}\div 10^{12}$ звезд, необходимо создать бесстолкновительную систему. Время двойного соударения в трехмерной системе равно [215]

$$T_c = {v^3_* \o 8\,\pi\,n\,G^2 m^2_* H\ln(R\,v^2_*/2\,G\,m_*)},$$ (3.1)

где $n$ - объемная концентрация звезд; $m_*$ - масса звезды; $v_*$ - относительная скорость; $R$ - размер системы; $H \simeq 0,\!4$ - геометрический фактор. Для галактик, за исключением самых центральных областей, время $T_c$ превышает возраст звездных систем. Поскольку $m_* \propto N^{-1}_*$ и $n \propto N_*$, то выполняется пропорциональность $T_c \propto N_*$. В силу того, что $N \ll N_*$, частицами при моделировании галактик являются ``макрозвезды'' с массой, превышающей в $N_*/N$ раз массу реальных звезд <sup>3.2</sup>. И для обеспечения бесстолкновительности системы возникает необходимость в вышеупомянутом ``обрезании'' потенциала.

3.1.2 Построение экспериментальных моделей плоских галактик

Опишем достаточно простую модель дисковой галактики, основанную на численном интегрировании уравнений движения $N$ гравитационно взаимодействующих частиц с учетом внешнего поля, которое обусловлено заданным распределением вещества в балдже и гало. Считаем, что параметры сфероидальной подсистемы стационарны -- плотность материи в балдже $\varrho_b$ и гало $\varrho_h$ не меняются в процессе эволюции диска. Такую модель будем называть динамической моделью.

Динамика гравитирующих $N\!$-тел описывается системой уравнений

$${d^2\vec{r_i}\o dt^2} = \sum_{j}^{N}{\vec{f}_{ij}} + \vec{F}_s \,\,\,\,\,\,\, (i=1,...,N)\,,$$ (3.2)

где радиус-вектор $\vec{r}_i(t)$ определяет положение $i$-й частицы; $\vec{f}_{ij}$ -- сила взаимодействия между $i$-й и $j$-й частицами ($\!i\ne j\!$); сила $\vec{F}_s=~\vec{F}_b + \vec{F}_h$ обусловлена сфероидальной подсистемой балдж/гало.

Воспользуемся пространственным распределением объемной плотности в гало в виде

$$\varrho_h(\xi) = {\varrho_{h0}\o (1+\xi^2/a^2)^k} \,,$$ (3.3)

где $\xi=\vert\vec{r}\vert=\sqrt{r^2+z^2}$ -- радиальная сферическая координата. Выбор $k=1$ (так называемое квазиизотермическое гало) обеспечивает плоскую круговую скорость вращения $V_c={\rm const}$ в области преобладания гало. С увеличением $k$ возрастает относительная концентрация сферической компоненты к центру, что оказывает влияние, сходное с влиянием балджа.

Распределение вещества в гало (3.3) при $k=1$ с центральной плотностью $\Oo\varrho_{h0} = M_h/\left\{ 4\pi a^3 \left[R/a -{\rm arctg}(R/a)\right] \right\}$ дает для силы

$$\vec{F}_h(\vec{r}) = - {4\pi G a^3 \varrho_{h0} \o \xi^2}\... ...rm arctg}\left({\xi\o a}\right)\right\}\, {\vec{r}\o \xi} \,$$ (3.4)

и определяется пространственной шкалой $a$ и массой $M_h$ внутри сферы $\xi<R$.

Для описания распределения плотности в сферическом балдже используем модель Кинга:

$$\varrho_b=\left\{ \begin{array}{cl} \varrho_{b0}/\left[1... ...\max}\\ 0&,\ \ \xi > r_b^{\max}\,,\\ \end{array} \right.$$ (3.5)

для которой величина

$$\Oo M_b = 4\pi b^3 \varrho_{b0} \left\{ \ln \left[ r_b^{\m... ...right] - {r_b^{\max}/b\o \sqrt{1+(r_b^{\max}/b)^2}} \right\}$$ (3.6)

является массой балджа. Внутри $\xi \le r_{b}^{\max}$ для гравитационной силы имеем:

$$\vec{F}_b = - {4\pi G b^3 \varrho_{b0}\o \xi^2} \left\{ \l... ...i/b \o \sqrt{1 + \xi^2/b^2}} \right\} \, {\vec{r}\o \xi} \,.$$ (3.7)

Очевидно, в области $\!\!\xi>r_b^{\max}\!\!$ в случае (3.5) выполняется $\vec{F}_b =~- GM_b \vec{r}/\xi^3$. Для $\xi>r_{b}^{\max}$ рассматривалось обобщение закона (3.5) линейным или экспоненциальным (мы не приводим громоздкие формулы для этого случая) усечением с характерной шкалой $L_b$. Таким образом, масса балджа $M_b$ конечна, а масса гало $M_h(r)$ в соответствии с (3.3) увеличивается с ростом радиуса. У балджа в качестве подсистемы в некоторых моделях будем выделять ядро, плотность в котором $\varrho_c(\xi)$ также определяется законом (3.5) со шкалой $b_n < r_n^{\max}\ll b$.

Динамическая модель должна адекватно описывать ньютоновское взаимодействие между частицами и обеспечивать бесстолкновительность системы. Последнее достигается модификацией гравитационной силы на малых расстояниях, для чего вводится радиус обрезания потенциала $r_c$ между любыми двумя взаимодействующими частицами $i$ и $j$. Вопрос об оптимальном выборе радиуса обрезания и числа частиц неоднократно обсуждался в литературе (см., например, [261, 742, 743, 823] и ссылки в этих работах). Следует подчеркнуть, что обрезание потенциала -- единственная возможность обеспечить бесстолкновительность моделей галактик в рамках задачи $N\!$-тел. Если даже величина $r_c$ не фигурирует явно в численной схеме, как в случае $PM\!$-алгоритма (распространена точка зрения, что метод не содержит радиуса обрезания), она присутствует неявно -- ее роль играет характерный размер ячейки.

Простая модель Пламмера для потенциала

$$\Phi_{ij} = - G{m_i m_j\o \sqrt{r_{ij}^2 + r_c^2}} \,,$$ (3.8)

где $r_{ij}$ -- расстояние между двумя частицами; $r_c$ -- радиус обрезания, решает проблему обеспечения бесстолкновительности (рис. 3.8). Использование сплайн-ядра для смягчения силы тяготения дает преимущество по сравнению с (3.8), поскольку вне заданного радиуса ($r> 2r_c$) сила в этом случае в точности совпадает с Ньютоновской [576]. При фиксированном числе частиц $N$ всегда можно выбрать значение $r_c$, обеспечивающее бесстолкновительность модели. Но для уменьшения погрешности, связанной с изменением потенциала взаимодействия между частицами на малых расстояниях, их число должно быть достаточно велико.

Поверхностную плотность диска будем характеризовать шкалой $L$, которая определяет экспоненциальный закон 1.2, и в этом случае для массы диска имеем $M_d=2\pi L^2\sigma_0$, причем примерно 95 % массы диска сосредоточено внутри $r\le 4L$. Относительная масса гало рассчитывается внутри определенного радиуса $\mu(r) = M_h(r)/M_d$.

При расчетах удобно выбрать систему единиц, в которой $G=1$, $R=~4L=1$, масса диска $M_d=1$. Массу гало $M_h$ внутри радиуса $\xi \le 4L$ будем нормировать на массу диска $\mu\equiv M_h/M_d$. В этой системе единиц один период вращения диска по внешнему краю лежит в пределах $T_0\sim 3\div 4$ для значений $\mu=1\div 4$. Типичные значения скорости вращения -- $V\sim 1\div 2$, дисперсии радиальных скоростей -- $c_r\lee 1$, на периферии диска $c_r\ll 1$.

Опишем процедуру задания начального распределения плотности вдоль $z$-координаты и остаточных скоростей равновесного диска. Для задания частицам в начальный момент времени координат и скоростей удобно использовать сетку в цилиндрической системе координат. Координаты частицы внутри ячейки определяем с помощью трехкратного применения генератора случайных чисел. Выбрав закон изменения поверхностной плотности $\s_*(r)$, разобьем диск на достаточно узкие кольца шириной $\Delta r$ и по заданному $\s_*(r)$ вычислим число частиц $n_i$, попадающих в $k$-е кольцо. Так, в ``стандартной'' модели Острайкера и Пиблса [685] $\s_*(r) \propto r^{-1}$ и число $n_i = N\,\Delta r/R$, а в модели экспоненциального диска [ $\s_* \propto \exp(-r/L)$] число частиц в кольце равно

$$n_i = { N\, {\rm exp}(-i\,\Delta r/L) \o 1-(1+1/L)\,{\rm ... ...\big({\Delta r\o L}\big) - 1 \Big) - {\Delta r \o L} \Bigg\},$$ (3.9)

где $r_i = (i - 1/2)\,\Delta r$ -- средний радиус кольца ( $i = 1,\!2,\! ...$), $R=1$.

Каждое кольцо разделим на $n_i$ равных частей в азимутальном направлении и в каждую полученную таким образом ячейку поместим частицу. Координаты частицы внутри ячейки естественно определить с помощью двукратного применения генератора случайных чисел (один раз -- в радиальном направлении, второй -- в азимутальном), сопоставляя интервал изменения случайных чисел (обычно -- [$0,\,1$]) с шириной кольца $\Delta r$ и шириной сектора $r_i\Delta\varphi = 2\,\pi\, r_i/n_i$. После этого в каждом кольце вычисляем среднюю по $n_i$ частицам радиальную гравитационную силу $F_{ri}$, действующую на каждую частицу со стороны всех остальных частиц диска и статического гало (см. ниже). И всем частицам рассматриваемого кольца придаем азимутальную скорость $V^{(1)}_i = (r_i F_{ri})^{1/2}\!$. Ясно, что приготовленный таким образом диск является хотя и равновесным, но ``холодным'' и, следовательно, подверженным сильной гравитационной неустойчивости.

Вертикальная структура диска определяется уравнениями [77]:

$$\frac{\Vert\,(\varrho c_z^2)}{\Vert z} + \frac{\Vert\,(r\... ...{\Vert^2 \Phi \o \Vert z^2}= 4\pi G(\varrho + \varrho_s) \,,$$ (3.10)

где $\varrho$ и $\varrho_s$ -- соответственно объемная плотность вещества в дисковой и сфероидальной подсистемах; $c_z$ -- дисперсия вертикальных скоростей; $\alpha_{rz}=\langle uw \rangle$; скобки $\langle\ldots\rangle$ означают усреднение скоростей и $\alpha_{rz}$ обусловлено хаотическими составляющими радиальной скорости $u$ и вертикальной $w$. Исключая потенциал $\Phi$ в уравнениях (3.10), вводя круговую скорость

$$\Oo V_c(r) \equiv \sqrt{ r \left( {\Vert \Phi \o \Vert r} \right)_{\big\vert z=0}} \,,$$ (3.11)

для заданных величин $c_z$, $\alpha_{rz}$ можно перейти от системы дифференциальных уравнений в частных производных к приближенному уравнению для объемной плотности диска $\varrho(z)$ в форме обыкновенного дифференциального уравнения (считаем все производные по $r$ известными):

$$\varrho{d\o dz}\left( c_z^2 {d\varrho\o dz}\right) - c_z^... ...g) + \varrho^2\,\frac{d}{dz}\frac{E_\alpha}{\varrho} = 0 \,,$$ (3.12)

$$E=-{1\o 4\pi G r}{\Vert V^2_{c}\o \Vert r}\,, \ \ \ \ E_\alpha = \frac{\Vert(r\varrho\alpha_{rz})}{r\,\Vert r} \,,$$

которое совместно с условиями $\varrho(z=0) = \varrho_0$, $d\varrho(0)/dz=0$, $\int\limits_{-\infty}^{\infty}{\varrho(z;r)\,dz}=\sigma(r)$ для заданного распределения поверхностной плотности $\sigma$ определяет вертикальную структуру диска на фиксированном радиусе $r$. Для $c_z=$const и $\alpha_{rz}=0$ уравнение совпадает с рассмотренным в [266]. Третье слагаемое в (3.12) в случае слабой вертикальной неоднородности $c_z$ мало по сравнению с первыми двумя. В центре диска слагаемое $E$ может давать большую погрешность в оценке плотности, и на практике следует принимать $E(r\rightarrow 0)\rightarrow 0$. При заданных $\varrho_s(z,r)$, $c_z(z,r)$ и $\sigma(r)$ определяются $\varrho_0$ и $\varrho(z)$ по (3.12). После того, как найден закон распределения плотности вдоль $z$-координаты, частицы размещаются вдоль вертикальной оси на заданной сетке $z_k = k\, \Delta z$ ( $k=-K,\ldots, K$). В $k$-ю ячейку помещаются частицы в пропорции $\sigma_k/\sigma$, где $\Oo\sigma_k=\int_{z_{k-1}}^{z_k} \varrho(z)\, dz$.

Уравнение (3.12) имеет приближенный характер, поскольку введенная соотношением (3.11) величина $V_c$ не зависит от $z$-координаты. В исходном уравнении (3.10) слагаемое $\Oo\frac{1}{r}\frac{\Vert}{\Vert r}\left(r\frac{\Vert\Phi}{\Vert r} \right)$ в общем случае зависит от $z$-координаты. Поэтому при переходе к $V_c$ зависимость от вертикальной координаты теряется и далее величина $E$ (см. (3.12)) считается, что не зависит от $z$ (но параметрически зависит от $r$). Используемое приближение есть плата за переход от дифференциальных уравнений в частных производных (3.10) к обыкновенному дифференциальному уравнению (3.12). Нетрудно оценить, что относительная погрешность имеет порядок $(h/r)^2$ ($h$ -- вертикальная шкала диска).

Строго говоря, построенный таким образом диск не является равновесным. Отсутствие точного равновесия в вертикальном направлении играет роль небольшого дополнительного начального возмущения при изучении начальных неустойчивых состояний, которые эволюционируют к новому стационарному состоянию диска.

В случае $\Vert c_z/\Vert z=0$, $\varrho_s=0$, $V_c=\textrm{const}$, $E_\alpha=0$ решением уравнения (3.12) является

$$\Oo\varrho(z)= {\sigma\o 2z_0} \textrm{ch}^{-2}(z/z_0)$$ (3.13)

с характерной вертикальной шкалой $z_0=\sqrt{c_z^2/2\pi G\varrho(0)}= c_z^2/\pi G\sigma$. Закон (3.13) наряду с экспоненциальным

$$\varrho(z) = \varrho(0)\cdot \exp(-z/h_{exp})$$ (3.14)

часто используется для аппроксимации наблюдаемых профилей яркости для галактик, наблюдаемых с ребра ^3.3 [453, 560, 561]. На больших расстояниях от плоскости $z=0$ эти законы имеют одну асимптотику, и в этом случае $z_0\simeq 2h_{exp}\simeq 2h_{ch}$.

Полутолщину диска в численных моделях удобно характеризовать величиной

$$\Delta^2 = {\int^{\infty}_{-\infty}\,(z-\langle{z}\rangle)... ...varrho(z)\, dz \o \int^{\infty}_{-\infty} \varrho(z)\,dz} \,,$$ (3.15)

где $\!\langle\ldots\rangle\!$ -- усреднение по $z$. Определение параметра $\Delta$ в соответствии с (3.15) всего на 10 % отличается от полутолщины диска $z_0$, которая входит в закон вертикальной плотности (3.13). В работе [825] предложено определять вертикальную шкалу по медиане.

Начальная функция распределения по скоростям является шварцшильдовской, и представляет собой анизотропное максвелловское распределение:

$$f(u, v, w) = A\cdot \exp\left\{ -{u^2 \o 2\,c^2_r} - {(v-r\Omega)^2 \o 2\,c^2_\varphi} - {w^2 \o 2\,c^2_z}\right\}\,,$$ (3.16)

где $\{u,v,w\}$ -- компоненты скорости частиц в цилиндрической системе координат.

Средняя тангенциальная скорость точек для начального состояния модели находится из уравнения Джинса в предположении отсутствия систематического радиального движения, осесимметричности и симметрии относительно плоскости $z=0$ [862]:

$$V^2=(< v >)^2 = V_c^2 + c_r^2\, \left\{ 1 - {c_\varphi^2\o... ... r} + {r\o c_r^2}{\Vert \alpha_{rz} \o \Vert z} \right\} \,,$$ (3.17)

где круговую скорость $V_c$ в плоскости $z=0$ определяют распределения вещества в трех основных компонентах: диске, балдже и гало. В результате имеем

$$V_c = \sqrt{ (V_c^{disc})^2+(V_c^{bulge})^2+(V_c^{halo})^2 } \,,$$ (3.18)

где $V_c^{disc}$, $V_c^{bulge}$, $V_c^{halo}$ -- соответствующий вклад в круговую скорость от отдельных компонент. При задании начального состояния модели можно принять $\langle u\rangle=0$, $\langle w\rangle=0$, а скорость вращения $V\equiv\, \langle v\rangle$ задавать в соответствии с (3.17). Таким образом, в начальный момент времени имеется баланс радиальных и вертикальных сил, и диск начинает эволюцию с состояния, близкого к равновесному. В начальный момент времени диск имеет конечную ``температуру'', которая определяется тремя функциями $c_r(r)$, $c_\varphi(r)$, $c_z(r)$. Конкретный вид этих зависимостей диктуется постановкой задачи.

Частицам рассматриваемой ячейки придаем азимутальную скорость, равную круговой (3.11). В результате получаем холодный диск. На следующем этапе, исходя из заданных величин $\!c_r\!$, $\!c_\varphi\!$, $\!c_z\!$, генерируем случайные скорости частиц в соответствии с распределением (3.16). Наконец, с учетом (3.17), уточняем скорость вращения в зависимости от конечной толщины и теплового разброса скоростей. На заключительном этапе корректируем положения частиц и их скорости так, чтобы центр масс и кинематический центр совпадали с центром координат ^3.4.

Отличительной особенностью звездных бесстолкновительных дисков является анизотропия дисперсий скоростей звезд: $c_r\ne c_\varphi\ne c_z$ [420], причем $c_r>c_\varphi>c_z$. Дисперсии компонент остаточных скоростей звезд $c_{r,\,\varphi,\,z}$ малы по сравнению со скоростью вращения звезд диска $V\!\!$, кроме центральных областей $r\le L$, где возможно $c_r > V$ ^3.5. Поэтому при осесимметричном распределении вещества справедливо эпициклическое приближение, когда равновесие диска в радиальном направлении обусловлено прежде всего балансом центробежной и гравитационной сил с точностью до слагаемых $\sim (c_r/V)^2$ (см. (3.17)). При вращении частиц на радиусе $r$ с учетом эпициклического движения имеем связь между $c_\varphi$ и $c_r$:

$$c_r=\frac{2\Omega}{\varkappa}\cdot c_\varphi \quad {\tex... ...{\varkappa(r)}{2\Omega(r)}\frac{c_r(r)}{c_\varphi(r)} = 1 \,,$$ (3.19)

где $\varkappa=2\Omega\sqrt{1+r\,d\Omega/2\Omega\,dr}$ -- эпициклическая частота. Следует подчеркнуть, что в динамических моделях условие (3.19) выполняется для угловой скорости вращения частиц $\Omega=V/r$, а не для круговой скорости (3.11). Выполнение $Q_c=1$ является необходимым условием бесстолкновительности динамических моделей.

В результате выполнения всех этих процедур получаем модель ``горячего'' звездного диска конечной толщины, в которой необходимо еще скорректировать координаты частиц и их скорости таким образом, чтобы центр масс системы частиц в ходе эксперимента оставался в начале координат.

При постановке экспериментов, в которых помимо диска плоской галактики моделируется и ее сферическая подсистема (гало), необходимо учесть, что дисперсия скоростей звезд гало значительно превышает дисперсию скоростей звезд диска ([406, 651], гл. 1). В то же время величина возмущений плотности всякой подсистемы обратно пропорциональна квадрату ее дисперсии скоростей ([586], п. 2.2.2). Поэтому в процессе эволюции диска, не меняющей существенно распределение масс в нем, гало можно считать невозмущающимся и моделировать потенциалом $\Phi_h(r)$, действующим на звезды диска.

Взаимодействие частиц в диске. Взаимодействие частиц друг с другом должно, очевидно, моделировать основные свойства звездного диска как бесстолкновительной гравитирующей системы. Конструктивное в экспериментальном плане определение бесстолкновительности диска можно сформулировать следующим образом: сила, действующая на данную частицу со стороны всех остальных частиц диска, должна быть заметно больше силы, действующей на ту же частицу со стороны ее ближайшей соседки. Это определение естественным образом приводит к необходимости ``обрезания'' гравитационного взаимодействия частиц на малых расстояниях, что использовалось во всех численных экспериментах. Для оценки величины соответствующего параметра определим ``радиус взаимодействия'' $r_\textrm{вз}$ соотношением

$$M_d(r)/r^2 = m/r^2_\textrm{вз}, %\eqno(3.1.7)$$ (3.20)

где $m = 1/N$ -- масса частицы; $M_d(r)$ -- масса диска в сфере радиусом $r$. Для экспоненциального диска

$${r_\textrm{вз} \o L} = { (r/L) \o \sqrt{N} } \sqrt{ {1 - (1 + R/L)\,\exp\{-R/L\} \o 1 - (1 + r/L)\,\exp\{-r/L\} } }.$$ (3.21)

По данным наблюдений, в дисках галактик $L/R \simeq 0,\!2 \div 0,\!3$ [560] и в этом случае зависимость $r_\textrm{вз}$ от радиальной координаты слабо отличается от линейной. Так, при $L = 0,\!25\,R$ соотношение (3.21) в области $r < R$ можно аппроксимировать функцией $\Oo r_\textrm{вз} \simeq {L \o \sqrt{N}}\left\{1,\!24 + 0,\!67\,{r \o L}\right\}$. Предположим теперь, что ``обрезание'' гравитационного взаимодействия на малых расстояниях мы осуществляем, вычисляя силу, действующую на $i$-ю частицу со стороны $j$-й частицы, следующим образом [685]:

$$\vec f_{i,j} = {1 \o N^2}{(\vec r_j - \vec r_i) \o \{(\vec r_j - \vec r_i)^2 + r^2_c\}^{3/2}}, %\eqno(3.1.10)$$ (3.22)

где $r_c$ -- радиус ``обрезания'' взаимодействия. Конкретный выбор $r_c$ зависит, очевидно, от целей эксперимента. Так, при изучении формирования бар-моды в центральной части диска Острайкером и Пиблсом было найдено оптимальное значение $r_c \simeq 0,\!05$ при малом $N = 150 \div 500\!$. Чем более мелкомасштабные структуры изучаются, тем меньше должен быть $r_c$, сохраняя, однако, бесстолкновительность системы. Приемлемым в экспериментальном плане является $r_c \simeq (1 \div 3)\,r_\textrm{вз}\!$. Важно отметить, что полагать величину $r_c$ зависящей от радиальной координаты в конкретном эксперименте нельзя, поскольку в этом случае энергия системы не будет интегралом движения.

Наглядную информацию при изучении спиральных и бароподобных структур дает фурье-анализ поверхностной плотности в координатах $\varphi$ и $\ln(r)\!$. Уровень неосесимметричности радиально неоднородного распределения вещества в диске в каждый момент времени удобно характеризовать амплитудой фурье-гармоник [781]

$$A(t;p,m)= {1\o N} \sum\limits_{j=1}^{N} \exp\bigg\{\, i\, \Big[ m\varphi_j(t) + p \ln (r_j(t)) \Big] \bigg\}\,,$$ (3.23)

здесь $i=\sqrt{-1}$, а $p$ и $m$ характеризуют структуру возмущений соответственно в радиальном и азимутальном направлениях. Величины ${A}(t;p,2)$ определяют амплитуду двухрукавной моды $m=2$ и, в частности, бара, для которого максимальны гармоники с $p=0$. Параметр $p$ характеризует степень закрученности волн. Введем также интегральные амплитуды фурье-гармоник

$$\hat{A}(t;m) = \sqrt{ \sum_{p} \vert A(p,m)\vert^2} \,,$$ (3.24)

которые показывают, какие азимутальные номера мод преимущественно характеризуют глобальную структуру возмущений. Закон сохранения массы диска дает условие ${A}(t;0,0)=1$, а изменение величины $\hat{A}(t;0)$ со временем указывает на перераспределение вещества в радиальном направлении.

Следует еще отметить, что в описанных выше моделях плоских галактик число частиц невелико. Поэтому полученные в ходе обработки результатов значения локальных параметров диска испытывают со временем довольно заметные флуктуации. Однако если целью эксперимента является изучение характеристик стационарного диска, то влияние указанных флуктуаций может быть существенно уменьшено, если конечные результаты получать посредством усреднения по достаточно большому промежутку времени $t_s$ (порядка времени оборота диска). При таком подходе число частиц, эффективно участвующих в эксперименте, достигает величины $nN$, где $n = t_s/\tau \gg 1$ ($\tau$ -- величина шага по времени при интегрировании системы уравнений движения частиц).

3.2 Кpупномасштабная стpуктуpа звездных дисков

3.2.1 ``Глобальный'' критерий устойчивости

Рассмотрим результаты экспериментов со звездным диском без гало ($\!M_h = 0\!$). В таких системах интересные процессы протекают в центральной части диска. Проследим эволюцию первоначально осесимметричной системы, находящейся в основном на балансе гравитационной и центробежной сил ( $c_r \ll V_{\textrm{вр}}$, см. (3.17)). Такая система оказывается неустойчивой, и ее развитие заключается в росте дисперсии скоростей частиц. Одновременно происходит перераспределение плотности вещества, скорости вращения и искажение осесимметричной формы диска в бароподобную.

По-видимому, первая экспериментальная попытка охарактеризовать устойчивое стационарное состояние бесстолкновительного гравитирующего диска одним ``глобальным'' параметром была предпринята Острайкером и Пиблсом [685]. В качестве такого параметра ими была выбрана величина, равная половине доли кинетической энергии частиц системы, приходящейся на их среднее (макроскопическое) движение. Поскольку для гравитирующих систем справедлива теорема вириала в форме $2T + W = 0$, где $T$ -- кинетическая, а $W$ -- потенциальная энергия системы, то упомянутый параметр можно записать в виде

$$t_m = {T_{\textrm{ср}} \o \vert W\vert},\qquad (0 \le t \le 1/2),$$ (3.25)

где

$$T_{\textrm{ср}} = {1 \o 2}\int \langle\vec v(r)\rangle^2 f... ...)\, d\vec v \o \int f(\vec r,\vec v)\,d\vec v}, %\eqno(3.2.2)$$ (3.26)

а $f(\vec r,\!\vec v)$ -- стационарная функция распределения звезд диска. Острайкер и Пиблс, однако, вместо $T_{\textrm{ср}}$ фактически вычисляли величину

$$T_{\textrm{вр}} = {1 \o 2}\int \langle v_\varphi (\vec r)\rangle^2 f(\vec r,\!\vec v)\, d\vec r\,d\vec v, %\eqno(3.2.3)$$ (3.27)

заметно отличающуюся от $T_{\textrm{ср}}$ в меньшую сторону, поскольку в моделях плоских галактик без сфероидальных подсистем весьма эффективным оказывается возбуждение крупномасштабного неосесимметричного возмущения в форме овала -- бар-моды, при котором среднее (макроскопическое) движение частиц-звезд оказывается существенно не круговым.

Примерно за один-два оборота первоначально холодный диск сильно разогревается, энергия вращательного движения переходит в энергию случайного движения, что приводит к

$$t_{ОР} \equiv T_{\textrm{вр}}/\vert W\vert \simeq 0,\!14 \pm 0,\!02.$$ (3.28)

Из (3.28) и теоремы вириала следует, что для устойчивости диска относительно глобальной бар-моды необходимо $T_{\textrm{вр}} < 0,\!28\,T$. Принимая для оценок $T_{\textrm{вр}}/T \sim V^2_{\textrm{вр}}/(V^2_{\textrm{вр}} + 3\,c^2_r)$, с учетом (3.28) получим $c_r \sim V_{\textrm{вр}}$. Последнее соотношение вытекает из глобального критерия устойчивости и нельзя забывать, что отношение $c_{r}/V_{\textrm{вр}}$ сильно зависит от радиальной координаты, падая с ростом $r\!$. В численных экспериментах без гало на периферии диска наблюдается $c_r/V_{\textrm{вр}} \simeq 0,\!5$ ([129, 130] и др.).

Экспериментальное вычисление параметра $t_m$, учитывающего некруговые движения частиц в диске, дает [129]

$$t_m \simeq 0,\!20 \pm 0,\!02. %\eqno(3.2.5)$$ (3.29)

Миллер и Смит [636] при изучении эволюции вращающегося бесстолкновительного шара к концу его второго оборота получили сплюснутый бар, в котором $t_m \simeq 0,\!21 \div 0,\!24$, а $t_{OP} \simeq 0,\!11$.

Результат (3.28) требует некоторого уточнения, связанного с тем, что теорема вириала для гравитирующих систем ( $\!2\,T + W = 0\!$) непосредственно к экспериментальным моделям не применима. Действительно, ньютоновский потенциал -- однородная функция $k = -1$ ($2\,T = k\,W$) степени координат [93]. Но используемый в экспериментальных моделях потенциал с мягким ``обрезанием'' гравитационного взаимодействия на малых расстояниях (см. п. 3.1.2) при $r < r_c$ ($r_c$ -- радиус ``обрезания'') близок к квадратичному потенциалу ($\!k = 2\!$). С учетом того, что $r_c \ll R$ ($\!R$ -- радиус диска), можно считать, что в среднем по диску $k = -1 + \varepsilon$, где $0 < \varepsilon \ll 1$. Тогда $2\,T + W \simeq 2\,\varepsilon\,E < 0$, $E = T + W < 0$ -- энергия системы. Сравнивая экспериментальные значения величин $t_{OP}$ и $t_{\textrm{вр}} \equiv T_{\textrm{вр}}/2\,T$, можно оценить $\varepsilon$. По результатам экспериментов [129, 130], $\varepsilon \simeq 0,\!09$.

Представляет интерес вопрос о влиянии начального распределения поверхностной плотности $\s_{*0}(r)$ на устойчивость бар-моды. Суммируя результаты многочисленных экспериментов, можно сказать, что модели, для которых в начальный момент времени характерна не очень высокая степень концентрации массы к центру диска, укладываются по параметру $t_{OP}$ в рамки, указанные Острайкером и Пиблсом (см. (3.28)). В моделях с более плотной центральной частью диска величины $t_{OP}$, $t_{\textrm{вр}}$, $t_m$ к концу экспериментов оказываются меньшими. Этот эффект связан, по-видимому, с большей интенсивностью релаксационных процессов в более плотных системах. В экспериментах, стартующих из состояний с начальной дисперсией радиальных скоростей $c_r(r) = 1,\!5 \cdot (2 \Omega/\varkappa)\cdot c_T$ (такой диск должен быть гравитационно устойчив относительно мелкомасштабных возмущений (см. § 2.3)), конечное значение параметра $t_m$ оказывается таким же, что и в экспериментах с $c_r(r) = (2\Omega/\varkappa)\cdot c_T$^3.6. Но с увеличением $c_r$ степень бароподобного искажения диска несколько уменьшается, а $t_{\textrm{вр}}$ увеличивается примерно на $10~\%$.

Соотношения (3.28), (3.29) означают, что плоские гравитирующие системы без сфероидальных подсистем в стационарном состоянии должны быть достаточно ``горячими'' -- в пекулярных движениях звезд должно быть заключено более половины их кинетической энергии. В таких системах, как правило, возбуждается бар-мода, а дисперсия радиальных скоростей частиц даже на периферии диска не меньше половины величины круговой скорости вращения его вещества.

3.2.2 Устойчивость диска относительно возбуждения бар-моды

Начиная с классификации галактик Хаббла, стало ясно, что плоские спиральные галактики можно разделить на две группы. Для одной из них (SB) характерно наличие яркой перемычки (бара) с прикрепленными к его концам (часто почти под прямым углом) спиралями. В другой группе плоских галактик ( S) спирали отходят от образования, расположенного в центре галактики. Ясно, что исследование устойчивости гравитирующего диска (аналитическое и численно-экспериментальное) должно определить те факторы, которые препятствуют возбуждению бар-моды во многих плоских галактиках.

Поскольку бар-мода является крупномасштабным возмущением, использованное в главе 2 коротковолновое приближение для изучения его устойчивости неприменимо. Таким образом, в этом случае необходимо учитывать структуру диска в целом, что, естественно, накладывает достаточно жесткие ограничения на свойства модели. Поэтому детальное аналитическое исследование устойчивости глобальной бар-моды (ГБМ) было проведено лишь в моделях твердотельно вращающихся дисков [146, 173, 525, 526]. Эти исследования показали, что модели тонкого диска без учета массы сферической подсистемы устойчивы относительно возбуждения бар-моды только при

$$t_{OP} \,\lee\, 0,\!129. %\eqno(3.2.6)$$ (3.30)

Дифференциальность вращения диска, по-видимому, слабо влияет на условия возбуждения бар-моды [420]. Тогда результат (3.30) означает, что устойчивыми относительно бар-моды могут быть только очень горячие диски -- такие, в которых кинетическая энергия вращения составляет менее трети полной кинетической энергии вещества диска. Ясно, что данные наблюдений не дают оснований надеяться на существование таких систем.

Более конструктивной оказалась постановка задачи, в которой помимо конечной толщины диска учитывалось наличие и сфероидальной подсистемы. Так, в модели, состоящей из однородного гало (сфероидальной подсистемы) и однородного сплюснутого эллипсоида вращения (диска) с большой полуосью $R$ и малой полуосью $b < R$, было обнаружено [173], что в дисковом пределе ( $b/R \rightarrow 0$) эллипсоид устойчив относительно возбуждения бар-моды при

$$M_h / M_d \,\gee\, 1,\!1 \, , %\eqno(3.2.7)$$ (3.31)

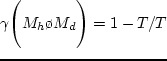где $M_d$ -- масса эллипсоида (диска); $M_h$ -- масса гало в сфере $r \le~R$. Учет конечного отношения $b/R$ понижает этот предел. Так, при $b/R =~0,\!05$ бар-мода не возбуждается уже при $M_h / M_d \,\gee\, 1,\!0$. Близкий к (3.31) результат ( $\!M_h/M_d \,\gee\, 1,\!18\!$) был получен и Бисноватым-Коганом [20] в модели с аналогичными макроскопическими характеристиками.

Как уже говорилось выше, аналитическое изучение устойчивости бар-моды в дифференциально вращающихся неоднородных дисках конечной толщины затруднительно. Это, очевидно, проще делать с помощью численного эксперимента. Ранние эксперименты (см., например, [487, 488, 685, 722]) подтвердили, что в недостаточно горячих ( $t_{OP} \,\gee\, 0,\!14 \pm 0,\!02$) тонких дисках без гало возбуждение бар-моды неизбежно. Учет конечной массы гало показал, что с ростом массы последнего бар-мода стабилизируется [256, 294, 350, 489, 515, 777, 826]. В то же время в разных моделях границы устойчивости бар-моды по параметру $M_h /M_d$ заметно различаются, группируясь, однако, в окрестности .

Результаты экспериментов удобно описывать с помощью параметра $\gamma = 1 - T_{\textrm{вр}}/T_{\textrm{ср}}\!$, характеризующего степень бароподобного искажения диска для различных распределений объемной плотности гало $\rho_h(r)$ [130]. В моделях без гало $\gamma \simeq 0,\!21 \div 0,\!26$ (рис. 3.3). С ростом массы гало параметр $\gamma$ уменьшается.

Figure: =10000 Зависимость $\Oo\gamma \Bigg({M_h\o M_d}\Bigg) = 1 - T_{\textrm{вр}}/ T_{\textrm{ср}}$, характеризующая степень развития бар-моды. В указанных на графике интервалах при каждом значении $M_h / M_d \neq 0$ -- результаты, полученные по четырем моделям, различающимся степенью концентрации гало к центру (в случае $M_h=0$ модели различаются начальным распределением поверхностной плотности)

=0.6

В связи с приведенными выше результатами представляет интерес и экспериментальный критерий [379], утверждающий, что для устойчивости диска относительно возбуждения бар-моды должно выполняться условие $\beta = (V_{\textrm{вр}})_{max}(L_\s / GM_d)^{1/2} \,\gee\, 1,\!1$, где ( $V_{\textrm{вр}})_{max}$ -- максимальное значение $V_{\textrm{вр}}$ в диске. По результатам экспериментов [130] этот критерий проверялся в конечных квазистационарных состояниях диска. Оказалось, что величина $\beta$ изменяется от $\beta \simeq 0,\!4$ при $M_h=0$ до $\beta \simeq 0,\!9$ при $M_h = 3M_d\!$. Таким образом, критерий [379] выглядит слишком жестким. Причина состоит, по-видимому, в том, что критерий был получен в экспериментах, в которых начальное состояние диска было холодным ($\!c_r = 0\!$). В таком состоянии условия возбуждения бар-моды наиболее благоприятны, а $(V_{\textrm{вр}})_{max}$ (измеряемое в начальный момент времени)  -- больше, чем в горячем диске. Кроме того, диски в экспериментах [379] двумерны, что также облегчает возбуждение бар-моды. Поэтому неудивительно, что указанный критерий приводит к необычайно низкой оценке отношения массы к светимости (порядка единицы) для дисков Sc-галактик [54]. Исходя же из результатов экспериментов [130], следует считать, что звездный диск устойчив относительно возбуждения бар-моды при $\beta \,\gee\, 0,\!7\!$.

В работе [343] обсуждалось условие $\alpha = {\cal L}\Omega_J/2\vert U\vert< 0,\!25$, здесь ${\cal L}$ -- полный угловой момент; $\Omega_J$ -- джинсовская частота. В эти критерии входят ненаблюдаемые параметры. В связи с появлением многочисленных данных по определению пространственных полей скоростей и дисперсий скоростей в галактиках удобнее переформулировать критерий стабилизации ГБМ в виде $c_r/V_{\max} > (c_r/V_{\max})_{crit}$, где $c_r$ -- дисперсия радиальных скоростей звезд на некотором фиксированном радиусе; $V_{\max}$ -- максимальная скорость вращения. Пусть внутри сферы радиусом $R$ полная масса равна $M$. Простая оценка $0,\!14=~E_k/\vert U\vert\simeq {\Oo {1\o 2} {c_r^2+c_\varphi^2+c_z^2 \o GM/R}} \simeq {\Oo {1\o 2}{c_r^2\o V_{\max}^2}(1+\alpha_\varphi^2+\alpha_z^2)}$ при $\alpha_\varphi^2~=~c_\varphi^2/c_r^2~=~1/2$, $\alpha_z^2~=~c_z^2/c_r^2~=~1/4$ дает $c_r/V_{\max}~=~0,\!4$, что требует уточнения, поскольку и дисперсии скоростей, и кривая вращения радиально неоднородны, а у распределения массы отсутствует центральная симметрия.

В горячих системах условия для развития ГБМ ухудшаются. Поэтому, если дисперсия скоростей звезд превышает некоторое критическое значение $c^{crit}\!$, то первоначально осесимметричный диск оказывается устойчивым. Наиболее удобно записывать такое условие для дисперсии радиальных скоростей $c_r$, поскольку дисперсия азимутальных скоростей с очень хорошей точностью равна $c_\varphi = c_r\,{\varkappa}/{2\Omega}$ ( $\Omega={V}/{r}$ -- угловая скорость вращения звезд).

Figure: Отношение $c_0/V_{\max}\!$, обеспечивающее стабилизацию глобальной бар-моды при различных массах гало в случае равенства шкал гало и диска $a=L$ для тонкого в начальный момент времени диска ( $\!\langle z_0\rangle/L=0,\!07\!$)

=0.5

Рассмотрим результаты динамического моделирования без балджа в приложении к галактикам позднего типа. Поскольку у гало следует считать $a\gee L$, то кривая вращения в таком потенциале имеет относительно протяженную область роста. Поэтому в центральной части диска () доминирует гравитационное влияние плоской подсистемы, что и определяет благоприятные условия для развития бар-моды. Даже преобладающее по массе гало $1\lee M_h \lee 2$ не способно подавить глобальную бар-моду, если диск достаточно холодный. И только, начиная с $M_h \gee 2$, при $a\simeq L$ ($M_h$ -- масса гало в пределах $r\le 4L$) гравитационная неустойчивость не приводит к формированию долгоживущей бар-структуры. В серии экспериментов изменялась только масса гало $M_h$ с пространственной шкалой $a=L$ и определялся радиальный профиль $c_r(r)$, стабилизирующий ГБМ. На рис. 3.4 показана зависимость отношения дисперсии радиальной скорости диска $c_0$, усредненная в зоне $r\le L$, к максимальной скорости вращения диска от относительной массы гало. В случае более рыхлого гало ($a\gee 2L$) образование бара возможно и при более массивной сфероидальной подсистеме. Значение $\mu^{crit}$ зависит от характера распределения плотности в гало -- в модели (3.3) от шкалы $a$. С ростом $a$ стабилизация бар-моды наступает при больших значениях $\mu$. При прочих равных условиях с увеличением толщины диска величина $\mu^{crit}$ уменьшается.

Если в начальный момент времени имеется экспоненциальный профиль и диск является достаточно холодным (в конечном состоянии дисперсия примерно в 1,5 раза выше начальной), то в результате формирования бара происходит заметное перераспределение вещества в диске. Отметим некоторые характерные особенности этого процесса:

1) Диск расплывается в радиальном направлении. Из области первоначально занимаемой веществом ($r\lee 4L$) может уходить до 30 % массы. Чем больше $M_h$, тем меньше массы уходит.

Figure: Радиальные зависимости поверхностной плотности диска для модели, ``стартующей'' с холодного состояния, в которой происходит существенное перераспределение плотности. Пунктирная линия 1 -- начальный экспоненциальный профиль; сплошная 2 -- конечный профиль, усредненный по азимуту, после сильного разогрева с образованием бара; штриховая линия 3 -- исходный профиль, обеспечивающий в конце расчета квазиэкспоненциальное распределение

=0.58

2) Результирующий профиль заметно отличается от экспоненциального, причем в центре ($r\lee 2L/3$) плотность увеличивается по сравнению с начальным, а далее уменьшается. Для получения экспоненциального профиля плотности необходимо задавать радиальные распределения специального вида (см. на рис. 3.5 пунктирную линию).

Структура бара, его размеры, отношение полуосей, а также кинематические характеристики в центральной области диска зависят не только от вида кривой вращения, но и от законов распределения вещества в дисковой и сфероидальных подсистемах, а также начальных условий. Поэтому понять свойства конкретной галактики в рамках общих моделей не всегда возможно, и часто требуется строить модели конкретного объекта.

Суммируя сказанное выше, можно утверждать, что у SB-галактик масса сферической подсистемы в целом должна быть меньше, чем у S-галактик. Косвенным подтверждением этого результата может служить тот факт, что вблизи центра скопления галактик в Волосах Вероники доля SB-галактик вдвое выше, чем на периферии скопления. Наиболее естественная причина этого -- в ``сдувании'' гало при взаимном сближении галактик и ослаблении вследствие этого устойчивости их дисков по отношению к возбуждению бар-моды [849]. Кроме того, фактором, способствующим формированию перемычки, может являться приливное взаимодействие со стороны массивного спутника [440].

3.2.3 Влияние газа на развитие бар-моды

В газовом самогравитирующем диске, как и в звездном, может развиваться бар-мода ^3.7. Однако из-за столкновительности газа неустойчивость (а она имеет гравитационную природу) проще стабилизировать, в отличие от бесстолкновительного звездного диска [см. (3.28)] достаточно выполнения $t_{OP} \,\lee\, 0,\!26$ [273]. Вандервоорт [869] в рамках линейного анализа устойчивости твердотельно вращающегося однородного звездно-газового сфероида показал, что критическое значение $t_{OP}$ лежит в пределах $0,\!14 \div 0,\!26$ в зависимости от параметров модели и прежде всего от доли массы газа в системе $\!M_g /(M_* + M_g)\!$.

Как мы знаем, галактический газ является сильно неоднородным на малых масштабах. Наблюдается целая иерархия газовых облаков, различающихся своими размерами и массами. В предыдущих пунктах мы уже видели, что на массивных газовых облаках (ГМО и более крупномасштабных образованиях -- ассоциациях) происходит эффективное рассеяние, переводящее орбитальное движение звезд и газа в тепловое. Таким образом, облачная структура газа является важным фактором стабилизации глобальных мод. Характерные времена образования и жизни облаков сравнимы со временем образования бара ( $\sim 5 \cdot 10^7$ лет). Поэтому для выяснения роли газа в подавлении бар-моды необходимо детальное рассмотрение процессов образования облаков, их динамики и звездообразования. Вклад в нагрев диска дает и динамическое трение: при движении тяжелых газовых облаков легкие звезды испытывают гравитационную фокусировку, образуя повышенную концентрацию за облаком.

Численные эксперименты, учитывающие вышеперечисленные эффекты, наглядно демонстрируют чрезвычайно важную роль газа в динамике звездного диска [471, 798]. Оказалось, что газ может стабилизировать бар-моду, если он составляет всего несколько процентов от общей массы. Разумеется, критическое значение величины $(M_g /M_*)_{crit}$ зависит от многочисленных параметров модели, однако, по-мнению авторов вышеперечисленных работ, для типичных галактик можно принять $(M_g/M_*)_{crit} \,\lee\, 10~\%$ (здесь следует учитывать газ и звезды, находящиеся в области формирования бара).

Обсудим подробнее этот результат. Для распределения поверхностной плотности в диске $\s = \s_0 /(1 +(r/a)^2)^{3/2}$ критерий устойчивости по порядку величины можно записать в виде [402]:

$$t_m \sim {M_d/M_{tot} \o 2\,(1 + 2\,\alpha^2)} < t_{crit} \simeq 0,\!1 \div 0,\!2 \, ,$$

здесь $M_{tot} = M_d + M_h$, $\alpha = c_r / \langle V_{\textrm{вр}}\rangle$, $\langle V_{\textrm{вр}}\rangle$ -- средняя скорость вращения, $c_r$ -- дисперсия радиальных скоростей на радиусе, где $V_{\textrm{вр}}$ достигает максимума. Учет столкновительности газа эффективно уменьшает массу диска $M_d$ на величину $M_g\!$. Однако более существенным фактором является разогрев звездной компоненты на массивных газовых облаках, что приводит к росту параметра $\alpha \propto D(t)$ со временем в соответствии с формулой (3.53). Характерный размер гигантских газовых облаков $r_G$ определяется гравитационной неустойчивостью, и величина $r_G$ пропорциональна поверхностной плотности газового диска $\s_g\!$. Учитывая, что масса облака $M_G \sim r^2_G \cdot \s_g \propto \s^3_g\!$, для параметра $\alpha$ можно записать

$$\alpha^2 \sim (\alpha^4_0 + {\rm const}\cdot \s^4_g\cdot t)^{1/2},\quad \alpha_0 = \alpha(t = 0).$$

Как видим, нагрев звездной подсистемы весьма сильно зависит от плотности газового диска и, как показывают численные эксперименты, в случае $\s_g \simeq 0,\!1 \cdot\s_*$ крупномасштабная гравитационная неустойчивость полностью стабилизируется. Следует не забывать, что к такому результату приводит совокупное самосогласованное действие фрагментации газа, звездообразования и всех релаксационных процессов.

3.2.4 Кинематика дисков с баром

В эпициклическом приближении (стационарный осесимметричный диск, у которого дисперсия мала по сравнению со скоростью вращения) имеется простая связь между компонентами дисперсии (3.19). Казалось бы в диске с баром эпициклическое приближение заведомо нарушается. Однако динамическое моделирование показывает, что в неосесимметричном диске с баром параметр не только в конце расчета в условиях квазистационарного состояния, но и на протяжении всей стадии образования бар-структуры (рис. 3.6), если при вычислении использовать средние по азимутальному углу параметры $c_r$, $c_\varphi$, $\Omega$ [539]. Имеем небольшие отклонения () вплоть до образования бара (см. рис. 3.6$\!$б, линия 1). В дальнейшем отклонения увеличиваются до 10 % на периферии из-за сильного утолщения диска в отсутствии гало (линия 3) в результате изгибов бара (см. п. 3.5.2). В моделях с массивным гало условие $Q_c=1$ выполняется лучше (рис. 3.6$\!$в).

Figure: Для модели с $M_h=0$, $M_b=0,\!1M_d$ зависимости параметра $Q_c$ на различных радиусах от времени (а); усредненные по времени радиальные распределения $Q_c$ (б) на интервалах: 1 -- $t=0\!-\!11$, 2 -- , 3 -- $t=11\!-\!20$; в) $Q_c(r)$ для модели при $\mu =1,5$; $a=L$. Показано положение малой и большой полуоси бара $r_{bar}^{minor}$, $r_{bar}^{major}$

=0.999

Каждая компонента дисперсии $c_r, c_\varphi , c_z$ скоростей имеет свое характерное распределение, которое является типичным для бар-моды независимо от условий эксперимента (рис. 3.7). Размеры ``бара'' параметра $c_r$ примерно в 2 раза меньше, чем по поверхностной плотности. Пространственное распределение дисперсии азимутальной скорости $c_\varphi$ заметно отличается от $c_r(x,y)$ из-за характерной перпендикулярной структуры в центре. Дисперсия вертикальной скорости в меньшей степени обнаруживает отличия от симметрии, за исключением самого центра.

Figure: Изолинии $c_\varphi$ и $c_r$ в центральной области бара

=0.28

Дисперсия скоростей вдоль луча зрения зависит от ориентации диска и бара

$$c^{obs} = \sqrt{c_z^2 \cos^2(i) + c_\varphi^2 \sin^2(i) \cos^2(\alpha) + c_r^2 \sin^2(i) \sin^2(\alpha)} \,,$$ (3.32)

где $\alpha$ -- угол между щелью и большой осью в плоскости галактики. Если большие оси бара и галактики совпадают, то поле дисперсии не обнаруживает бар-образования [539]. При других ориентациях бара и большой оси галактики заметны вытянутые образования на поле $c^{obs}\!$. ``Бар-структура'' дисперсии скоростей во всех случаях имеет маленькие размеры по сравнению с баром поверхностной плотности. При прочих равных условиях ``бар дисперсии скоростей'' более заметен при больших углах наклона $i$, что связано с уменьшением вклада дисперсии вертикальной скорости $c_z$ в $c^{obs}\!$.

Figure: =0.9I<>а) -  cтруктура течения газа в области бара. Изображены изолинии радиальной скорости $U$. Пунктирная линия -- $U=0$; б) - cхема радиальной скорости звезд (стрелки) в области бара (показаны изолинии поверхностной плотности) по результатам динамического моделирования

true cm true cm

=0.28

Figure: Распределение компонент скорости вещества в области бара по результатам динамического моделирования: а) - радиальная скорость $U$, отличающимся цветом показаны области, где $U>0$ и $U<0$; б) - изолинии азимутальной скорости $V$; в) - функция $V(x,y)$, стрелка сонаправлена с большой осью бара

=0.5

В области бара движение газа и звезд является существенно некруговым. Поле скоростей имеет характерную четырехсекторную структуру (рис. 3.8). На рис. 3.9 для модели звездного диска с отношением осей у бара показаны изолинии радиальной компоненты скорости $U$ (рис. 3.9$\!$а) и азимутальной скорости $V$ (рис. 3.9$\!$б) в плоскости диска. Функция $V(x,y)$ имеет характерный седлообразный вид (рис. 3.9$\!$в). Кривая вращения $V(r)$ часто используется для определения закона распределения массы в галактике. В области бара такой подход неприменим, поскольку поле скоростей сильно неоднородно по азимутальному углу, имеются значительные радиальные движения, и оценки на основе баланса гравитационной и центробежной сил крайне неточны. Профили скорости вдоль большой и малой осей качественно различаются (рис. 3.9$\!$в), причем азимутальная неоднородность $V$ может быть очень значительной (рис. 3.10).

Figure: Зависимость азимутальной компоненты скорости $V$ от расстояния до центра вдоль большой и малой осей бара (модель с тонким холодным в начальный момент времени диском при ; $a=0,\!5$; $M_b=0,\!3$; $b=0,\!02$). Вклад в столь сильную азимутальную неоднородность $V$ вносит также отклонение радиального профиля поверхностной плотности от экспоненциального -- см. увеличение $\sigma$ в центре на рис. 3.5

=0.45

Вращение бара. Во многих галактиках центральная часть выглядит как сложная система, состоящая из нескольких вложенных друг в друга компонент (бары, диски, кольца, двойные ядра) [235, 788, 807]. К их числу относятся так называемые ``мини-бары'' -- большая полуось $r_{bar}^{major}$ таких структур лежит в пределах нескольких сотен парсек. Примерами галактик с мини-барами являются NGC 4736 с $r_{bar}^{major}=225$ пк [882], NGC 81 ( $r_{bar}^{major}=0,5$ кпк) [532], UGC 5600 [789].

Размеры бара связаны с угловой скоростью его вращения $\Omega_{bar}$. На рис. 3.11 на примере галактики NGC 936 изображены радиальные зависимости угловой скорости вращения диска $\Omega(r)$ и частот $\Omega^{(m)}(r)=~\Omega-~\varkappa/m$ ($m=2,4$, $\varkappa$ -- эпициклическая частота). Выделяют три типа баров, которые различаются угловой скоростью вращения и размерами [697, 711]:

1) быстрые бары с $\Omega_{bar}> \Omega^{(2)}$;

2) медленные бары с $\Omega_{bar}< \Omega^{(2)}$;

3) промежуточные с $\Omega_{bar}\simeq \Omega^{(2)}$.

Figure: Распределения в диске угловой скорости вращения $\Omega$, эпициклической частоты $\varkappa\!$ и линдбладовских резонансов $\Omega-\varkappa/m$ ($m=2,4$) на примере модели NGC 936. Приведена угловая скорость вращения бара в модели $\Omega _{bar}=64$ км/с/кпк и ограничения из наблюдений $\Omega _{bar}^{obs}=~60\pm 14$ км/с/кпк [642]
Figure: Изолинии поверхностной плотности в динамической модели с баром промежуточного типа с угловой скоростью $\Omega _{bar}=\Omega ^{(2)}$

=0.49

=0.47

Быстрые бары, формирующиеся в результате неустойчивости глобальной бар-моды, хорошо известны, начиная с классической работы Острайкера и Пиблса [685]. В рамках моделей N-тел исследованы медленные бары [167], пример промежуточного типа показан на рис. 3.12.

В случае маломассивных балджей кривая вращения диска имеет относительно протяженный твердотельный участок, на котором вещество диска вращается с частотой $\Omega_0$. В среднем отношение $\Omega_{bar}/\Omega_0$ близко к 0,5. Массивные и концентрированные балджи приводят к более короткому твердотельному участку вращения диска. Угловая скорость вращения вещества в центре $\Omega_0$ увеличивается, поэтому возможно .

Динамические модели показывают, что при прочих равных условиях в более горячих системах бар вращается медленнее. Этот результат, возможно, обусловлен дополнительным вкладом неустойчивости радиальных орбит, который более эффективен в горячих системах и приводит к медленным барам [166].

Следует сказать, что бар-мода не является единственным механизмом формирования бара. В случае медленного вращения системы ( $\!c_{r} \gg~V_{\textrm{вр}}\!$) возникают условия для развития неустойчивости радиальных орбит [420]. Результатом развития этой неустойчивости могут являться перемычки в галактиках с массивным балджем и мини-бары размером несколько сотен парсек в центре ряда плоских галактик [52, 166].

3.2.5 Центральная депрессия звездной плотности

В главе 1 упоминалось о таком локальном феномене, как депрессия (``дыра'') в распределении поверхностной плотности в центральных частях звездных дисков галактик. Возникает естественный вопрос, почему центральная депрессия плотности звездного диска не исчезает под влиянием релаксационных процессов, обусловленных коллективными процессами. В рамках численного эксперимента эта проблема рассматривалась в работах [58, 108, 110].

Для описания динамической эволюции глубины депрессии удобна величина

$$\Sigma(t) = 1 - {\s_*(r = 0,\!t) \o \s_{*max}(r_{max},\!t)},$$ (3.33)

где $\s_{*max}(r_{max},\!t)$ -- максимальное значение поверхностной плотности, а $r_{max}$ -- радиус, на котором этот максимум достигается. Моделирование показывает, что длительное существование депрессии в звездном диске возможно в системах с массивным гало ( $\!M_h \,\gee\, M_d\!$), обладающим, как правило, концентрированным ядром. Маломассивный сферический компонент с $M_h \,\lee\, M_d$ практически не сдерживает процесс диссипации центральной депрессии (рис. 3.13). При $M_h = 0,\!5\,M_d$ и $a = 0,\!01$ центральная ``дыра'' замывается практически сразу через $0,\!5 \div 1$ оборота звездного диска. Массивная сферическая компонента может даже усиливать центральную депрессию плотности. Так, например, при $M_h / M_d = 2$, $a = 0,\!01$ величина $\Sigma$ приближается к значению $0,\!8$ (рис. 3.13). Однако этот эффект сильно зависит не только от полной массы гало, но и от характера распределения вещества в нем. При ``рыхлом'' ядре ( $\!a = 0,\!2\!$) депрессия начинает усиливаться только при $M_h / M_d \,\gee\, 6\!$.

Figure: Временная эволюция глубины депрессии $\Sigma (t)$ (время нормировано на период обращения диска) в случае ``точечного'' ядра гало $a = 0,\!01$ для различных значений массы сферической подсистемы: 1 --  $M_h = 0,\!5\,M_d$; 2 -- $M_h=M_d$; 3 -- $M_h = 1,\!5\,M_d$; 4 -- $M_h = 2M_d$

=0.52

Таким образом, из описанных выше экспериментов следует, что только галактики с массивной и(или) достаточно концентрированной к центру сферической составляющей могут иметь депрессию звездной плотности. Фактически выживание депрессии в диске зависит от наличия массивного балджа, что согласуется с наблюдениями ряда реальных галактик (см. § 1.1). Заметим, что впервые на возможность существования ``дефицита'' поверхностной плотности во внутренней части плоской звездной подсистемы при определенных значениях параметров сферической подсистемы указывалось в работе [140], где этот вывод был сделан на основе расчетов равновесия вращающегося диска в поле гало.

В некоторых случаях наблюдения допускают наличие центральной депрессии плотности диска у галактик поздних морфологических типов, у которых балдж практически отсутствует, но имеется другая особенность -- перемычка. Поскольку бар вращается со скоростью, отличной от скорости вращения звездного диска, то это может приводить к перераспределению углового момента, что может сдерживать релаксацию центральной ``дыры''. По-видимому, в этом случае необходимо учитывать наряду со звездным диском и газовый. Причем бар не только может сдерживать релаксацию, но и быть ответственным за возникновение депрессии.

3.3 Звездные диски на границе гравитационной устойчивости

В данном параграфе методом динамического моделирования ($\!N\!$-тел) исследуются условия гравитационной устойчивости трехмерных звездных дисков в гравитационном поле стационарных сферических компонент -- балджа и гало. Основной целью является поиск минимально допустимых локальных значений дисперсии скоростей звезд в дисках галактик с различным распределением масс, при которых достигается квазистационарное состояние трехмерных дисков, начавших эволюцию со слабо неустойчивых равновесных состояний.

3.3.1 Проблема гравитационной устойчивости дисков
и критерии устойчивости

Теоретический анализ проблемы устойчивости вращающихся тонких дисков к различного рода возмущениям (включая и изгибные) подробно рассмотрен в монографиях Поляченко и Фридмана [163, 420]. Аналитический подход к рассмотрению динамики возмущений в гравитирующем диске и определению условия устойчивости имеет наряду с преимуществом перед методом численного моделирования (математическая строгость решения в рамках поставленной задачи) тот недостаток, что реализуется только в рамках сильно упрощенных моделей, и в приложении к реальным объектам может дать лишь грубую оценку параметров дисковой компоненты.

Рассмотрим эти упрощения подробнее. Прежде всего, в основе простых аналитических моделей бесстолкновительных дисков, рассматриваемых при анализе устойчивости, обычно лежит предположение о малой толщине диска -- фактически рассматривается бесконечно тонкий слой. Несмотря на малость отношений $h/r$ и $h/L$ ($r$ - радиальная координата; $h$ и $L$ - характерные вертикальная и радиальная шкалы соответственно) для большей части звездного диска, это условие может быть недостаточным для того, чтобы пренебречь вертикальными движениями (подробное обсуждение этого вопроса, как и вывод о том, что в общем случае уравнения динамики астрофизических дисков не могут рассматриваться в двумерной постановке задачи, см. Приложение II в книге Горькавого и Фридмана [36] и в [198]).

При аналитических исследованиях динамики малых возмущений в звездном диске обычно исходят из малости радиальных градиентов параметров диска (см., например, [585, 851, 866]). Попытки учета градиентных факторов проводились только в рамках ВКБ-приближения (например, [126, 130, 141]). Это означает, что характерная длина волны возмущений должна быть малой по сравнению с локальными масштабами неоднородности равновесной скорости вращения $V(r)$, дисперсии радиальных скоростей звезд $c_r(r)$ и поверхностной плотности $\sigma(r)$. Во многих случаях эти условия выполняются с малым запасом или даже нарушаются. Пожалуй, особую трудность представляет дифференциальность вращения. Учет слабой неоднородности угловой скорости вращения возможен для слабо-нерадиальных возмущений [126, 128]. Однако более неустойчивыми являются сильно неосесимметричные (в пределе --``спицеобразные'') возмущения. Для их стабилизации при прочих равных условиях требуется существенно более сильный разогрев диска, то есть более высокая дисперсия скоростей звезд [169], и именно они, по-видимому, приводят на нелинейной стадии к увеличению дисперсии скоростей звезд в случае первоначально холодной системы.

При аналитических исследованиях гравитационной устойчивости дисков обычно используется эпициклическое приближение , которое для большинства галактик выполняется на периферии, где $c_r/V \simeq~0,\!1 \div 0,\!3$, но нарушается при приближении к центру, где $c_r \gee V$.

Другое важное ограничение аналитических подходов связано с локальным характером получаемых критериев. В то же время ряд исследований свидетельствует о глобальном характере условия устойчивости диска [388, 389]. Это означает, что если изменить равновесные параметры, например, в центре, сохранив их на периферии диска, то условие гравитационной устойчивости может измениться во всем диске. В рамках глобального анализа, в отличие от локального, основанного на анализе дисперсионных уравнений, собственная частота ищется для всего диска при решении задачи типа краевой, что и определяет возможность влияния условий в одной из частей системы на дисперсионные свойства возмущений во всем диске. Поэтому строгий подход требует рассмотрения диска как целого. Но глобальный анализ проведен только для специфических распределений степенного вида [388, 389, 783]. В применении к поддержанию долгоживущих спиральных волн плотности в галактиках глобальные моды в дисках рассматривались, например, в [295].

Численные эксперименты с бесстолкновительными системами более гибки к выбору модели. Они позволяют выйти за рамки локального анализа и простых двумерных моделей и непосредственно следить за развитием возмущений в первоначально равновесном диске. Однако этот подход также имеет свои недостатки. Наиболее серьезными проблемами при использовании метода $N\!$-тел являются, во-первых, определенные математические упрощения, неизбежные при любом способе представления диска системой $N$ гравитирующих тел, где $N$ несравнимо меньше числа звезд в реальных галактиках, а во-вторых, зависимость конечного состояния системы после ее прихода в квазистационарное состояние от задаваемых начальных параметров, которые для галактик плохо известны. При сопоставлении с реальными галактиками может также возникнуть проблема учета диссипативной среды (газа), скорость звука в которой существенно меньше дисперсии скоростей старых звезд.

В литературе встречается несколько критериев гравитационной устойчивости бесстолкновительных дисков, аналитически полученных в рамках различных моделей. Рассмотрим важнейшие из них.

=0.94

1) Критерий Тоомре. Для гравитационной устойчивости относительно осесимметричных возмущений бесконечно тонкого однородного твердотельно вращающегося звездного диска необходимо выполнение условия Тоомре [851] (2.83):

$$c_r \ge c_T={3,\!36\, G \sigma \o \varkappa} \,, {\ \ \ \textrm{или}\ \ \ } Q_T={c_r\o c_T} \ge 1 \,.$$ (3.34)

Условие (3.34) предполагает выполнение эпициклического приближения, когда различием между скоростью вращения диска $V(r)$ и круговой скоростью $V_c(r)$ можно пренебречь (3.17). Хотя (3.34) получено в рамках локального анализа, исследования собственных мод в рамках автомодельных дисков в соответствующем приближении, проведенные в работе Эванса и Рида [389], в целом подтверждает это соотношение. Миллер [633] провел сравнение теоретических инкрементов в рамках модели Тоомре с результатами моделирования осесимметричных мод -- для этого все остальные возмущения искусственно подавлялись. Было показано, что экспериментально определенные инкременты не противоречат теоретическим выводам.

2) Учет конечной толщины диска. Конечная толщина оказывает стабилизирующее влияние на гравитационную неустойчивость в плоскости диска [420, 866]. Обобщение критерия устойчивости Тоомре (3.34) на случай диска конечной толщины имеет вид (2.101) [126, 141]:

$$Q_T^{(1)} = {1\o 1+0,974 \Delta \varkappa/c_r} < 1 \,,$$ (3.35)

где $\Delta$ -- полутолщина изотермического самогравитирующего диска. Но это условие оказалось заведомо недостаточным для устойчивости сколько-нибудь реальных систем. Это стало ясно из первых численных экспериментов, выполненных еще в 70-80-е годы и показавших, что на периферии стационарных бесстолкновительных дисков $c_r \simeq (1,5 \div 5)\cdot c_T$ [487, 488, 515, 629, 630, 631, 633, 685].

3) Критерий с упрощенным учетом неосесимметричных возмущений. Одной из причин, по которой условие Тоомре оказывается недостаточным, является более сильная неустойчивость спиральных волн по сравнению с осесимметричными. В работах Поляченко, Шухмана и Калнайса [171, 420, 525] было впервые показано, что в гравитационно неустойчивом диске доминируют неаксиальносимметричные моды и эта проблема подробно рассмотрена в § 2.3, 2.4. Поскольку дисперсия азимутальных скоростей $c_\varphi$ меньше $c_r$ (за исключением самых центральных областей), то в силу соотношения (3.19) для стабилизации более холодного в азимутальном направлении диска требуется сильнее его разогреть, поэтому с учетом (3.19) условие (3.34) формально можно переписать в виде

$$Q_T^{(2)} \ge S \,, \ \ \ \ \ \ S = {2\Omega \o \varkappa} \,.$$ (3.36)

Параметр $S$ характеризует степень дифференциальности вращения диска. Исходя из наблюдаемых форм кривых вращения галактик, можно считать, что $1\le S\le 2$. Условие устойчивости в такой форме обсуждалось в работах [126, 141].

Таким образом, дисперсия азимутальных скоростей определяет упругость среды для сильно неосесимметричных возмущений, и для подавления гравитационной неустойчивости необходимо в $2\Omega /\varkappa$ раз сильнее разогреть диск. Критерий (3.36) можно назвать критерием Тоомре с упрощенным учетом неосесимметричных возмущений.

4) Критерий Морозова. В рамках ВКБ-приближения динамика слабо нерадиальных возмущений в неоднородном диске описана в § 2.2, 2.4, [126, 128, 141]. Критерий устойчивости (2.126), (2.127) учитывает большое число факторов (радиальные неоднородности поверхностной плотности $\sigma$ и $c_r$, толщину диска, дифференциальность вращения), и его также удобно записывать в виде $Q_T^{(M)}=c^{(M)}/c_T$ ($c^{(M)}$ определяется (2.127)). В общем случае нахождение $c^{(M)}$ сводится к интегрированию приведенного дифференциального уравнения (см. [111]). Дисперсионные ветви неосесимметричных возмущений и причина увеличения инкрементов гравитационной неустойчивости в неоднородном диске рассмотрены в [141]. Основным недостатком критерия является то, что он получен в результате динамики сильно закрученных спиральных волн ($m/r \ll k_r$, $k_r$ - радиальное волновое число), а затем произведен формальный переход к спицеобразным возмущениям.

Если считать, что характерный масштаб неоднородности $L_c\equiv\left\{ d\ln c^{(M)}/dr\right\}^{-1}$ является фиксированной величиной, то дифференциальное уравнение (2.130) сводится к алгебраическому соотношению (2.127) [126, 128, 141]. Для типичных форм кривых вращений $D\simeq 0,\!6\div 0,\!8$. Введением множителя можно формально учесть толщину диска и в критериях (3.36) и (3.37).

Figure: Зависимость $Q_T^{(P)}(\alpha )$. Данные для кривой 1 взяты из рис. 1 работы [169]. Зависимость 2 построена в соответствии с формулой (3.37). Плоская кривая вращения соответствует значению $\alpha =2$, что дает $Q_T^{(P)}(\alpha)=3,\!1$. При больших значениях $\alpha$ имеем случай твердотельного вращения

=0.55

5) Критерий Поляченко-Поляченко-Стрельникова. В отличие от рассмотренных выше, в работе Поляченко и др. [169] рассматривались предельно неосесимметричные возмущения в тонком диске. В этом случае граница устойчивости определяется исключительно кривой вращения, поскольку зависит только от параметра $n\equiv -{r\,d\Omega/(\Omega\, dr)}\!$. Зависимость безразмерной дисперсии радиальных скоростей на границе устойчивости от $\alpha = 2/n$ представлена на рис. 3.14 [169]. Для приложений можно пользоваться аппроксимирующей функцией

$$Q_T^{(P)}={c^{(P)}\o c_T} = 1,88\, \sqrt{ 1,1 + {8 \o \exp(\alpha - 1/4) - 1} }\,,$$ (3.37)

где $Q_T^{(P)}$ -- минимальное значение параметра Тоомре для устойчивого диска (рис. 3.14). Данная аппроксимация имеет достаточную для приложений точность в области $1,\!2< \alpha^2$. Критерий Поляченко и др. [169] является однопараметрическим, поскольку форма кривой вращения полностью определяет границу устойчивости. В частности, для области с постоянной скоростью вращения ($\!n = 1\!$) следует ожидать $Q_T^{(P)}\simeq 3$.

6) Учет газовой подсистемы при анализе устойчивости звездных дисков. Наличие более холодного компонента дает дополнительную дестабилизацию звездного диска. Этот вопрос был подробно рассмотрен в целом ряде работ [520, 521, 886], где анализировалась устойчивость звездно-газовых дисков относительно радиальных возмущений в линейном приближении (см. гл. 6). В [683] решалась более общая задача: исследовалось, как влияет на устойчивость тонкого диска к малым радиальным возмущениям неоднородность его состава, когда он состоит из частиц с определенным спектром масс, причем более массивные имеют меньшую дисперсию скоростей.

Задача упрощается, если масса ``холодного'' компонента относительно мала. Считая, что поверхностная плотность газа $\sigma_{gas}$ обычно значительно меньше, чем у звездного диска $\sigma_{star}$, и $c_s \ll c_r$ ($c_s$ -- адиабатическая скорость звука в газе), можно записать для дисперсии скоростей звездного диска, содержащего газ, на границе устойчивости [886]:

$${c_r^{crit} \o c_T} = 1+{\sigma_{gas} \o \sigma_{gas}+\sigma_{star}} {1-(c_s / c_T)^2 \o 1+(c_s / c_T)^2} \,.$$ (3.38)

Например, для параметров солнечной окрестности Галактики следует, что наличие газовой подсистемы, вклад от которой в поверхностную плотность диска составляет около 20 %, увеличивает в соответствии с (3.38) на $\lee 10$ % дисперсию скоростей звезд, достаточную для стабилизации радиальных возмущений.

Отметим, что для определения параметров дисковой подсистемы рассматривались также и другие подходы, основанные не на условиях локальной устойчивости, а на возможности существования в диске различных структур (спиральных волн плотности или бара), исходя из определенных механизмов их образования и поддержания (например, swing amplification [257, 258]).

7) Анализ гравитационной устойчивости диска в численных экспериментах. Численные эксперименты, описывающие динамическую эволюцию дисков, позволяют, задавая определенные начальные условия, исследовать неустойчивости диска с учетом неоднородности в распределении массы и угловой скорости. При этом естественным образом учитывается образование таких существенно нелинейных и неосесимметричных структур, как бар или транзиентные спирали. Сложностью такого подхода, однако, является зависимость результатов от начальных условий, поскольку эволюция диска, начинающаяся с сильно неустойчивого состояния, может происходить иначе, чем с субкритического уровня. К тому же диск может быть подвержен очень медленным секулярным неустойчивостям, которые трудно учесть в численных экспериментах.

Эволюционные модели $N\!$-тел обычно бывают нацелены либо на изучение характера развития неустойчивости, либо, что представляет в данном случае наибольший интерес, на анализ состояний системы по истечению многих оборотов диска. Из большого числа опубликованных работ мы упомянем с нашей точки зрения те, которые представляются наиболее важными для установления условий устойчивости диска.

Карлберг и Селвуд [338, 782] исследовали влияние малых нестационарных возмущений потенциала на эволюцию функции распределения скоростей. В частности, рассматривалось рассеяние на нестационарных спиральных волнах; полученное увеличение дисперсии скоростей звезд со временем хорошо согласуется с результатами численных экспериментов. Критическое значение дисперсии скоростей звездных дисков (параметр $Q_T$) неоднократно вычислялось по результатам динамического моделирования в рамках задачи $N\!$-тел (см., например, [111, 256, 338, 424, 488, 633, 773, 779, 780, 781, 784]). Ни в одном случае не был получен устойчивый диск с $Q_T < 1$. Как правило, на периферии диска параметр $Q_T(r)$ обнаруживает рост с расстоянием от центра. Данная особенность сохраняется и в экспериментах с трехмерными дисками [54, 273, 322, 324, 424, 786], и в некоторых теоретических исследованиях [705].

Классической считается работа Атанассулы и Селлвуда [256], которые пришли к выводу, что двумерный диск заведомо устойчив, если параметр Тоомре превышает значение $Q_T \gee 2,\!2\div 2,\!4$. Однако этот вывод был сделан без учета вертикальных движений. Трехмерные диски являются гравитационно более устойчивыми, поэтому двумерные модели приводят к недооценке массы маржинально устойчивого диска. Заметим также, что параметр $Q_T$ в работе [256] усреднялся по радиусу, а моделирование проводилось для специфического распределения поверхностной плотности -- использовалась модель Тоомре-Кузьмина. Поэтому возможность прямого приложения результатов этой работы к реальным трехмерным дискам галактик не очевидна.

3.3.2 Параметры звездных дисков на границе устойчивости

Недостаточно горячий диск является гравитационно неустойчивым. Его дальнейшая эволюция характеризуется разогревом, что выражается в росте дисперсий скоростей $c_r$, $c_\varphi$ частиц со временем. Обсудим результаты численных экспериментов по динамической эволюции дисков к устойчивому состоянию в зависимости от начальных значений $c_r(r)$ и $c_z(r)$, параметров балджа (3.5) и гало (3.3).

Отметим важнейшие особенности разогрева диска, полученные в численных экспериментах [207, 214].

Figure: Эволюция первоначально недостаточно горячего (неустойчивого) диска. Показана долговременная зависимость дисперсии радиальных скоростей от времени для 20 радиальных зон (1 -- центр диска, 20 -- на $r=4L$)

=0.38

1) Время разогрева диска в целом существенно больше среднего периода обращения частиц (3.15). На начальном этапе ($t\lee 1$) величина $c_r$ практически не меняется -- до тех пор, пока диск остается осесимметричным. В случае маломассивного гало эволюцию диска определяет глобальная бар-мода, и разогрев обусловлен процессом формирования неосесимметричной центральной перемычки и связанной с ней двухрукавной спиралью. Для моделей с достаточно массивным гало рост бар-моды не происходит, но образуется сложная транзиентная система мелкомасштабных спиральных волн, которые приводят к переходу кинетической энергии вращения в хаотическую компоненту скорости, то есть к нагреву диска.

2) Разогрев первоначально холодного диска ( $\!0,\!5\lee Q_T\lee 1\!$) начинается в центральной части. Процесс разогрева периферии происходит значительно медленнее. Увеличение дисперсии скоростей там обычно начинается, когда в центре уже достигается квазистационарное состояние. В то же время процессы в центре и на периферии оказываются взаимосвязанными: быстрая неустойчивость в центральной области способна ускорить разогрев внешней области диска, а ее устойчивость -- замедлять этот процесс.

3) Если не образуется бар, то c ростом дисперсии скоростей амплитуда возмущений начинает уменьшаться. В свою очередь, с уменьшением амплитуды волн замедляется и рост дисперсии радиальных скоростей $c_r\!$. Разогрев практически прекращается после затухания транзиентных спиральных волн. Интегральные амплитуды фурье-гармоник (3.24) для всех номеров мод $m$ со временем уменьшаются, но медленнее всех для $m=2$. Распределение плотности в диске становится близким к осесимметричному (если масса сферических компонент достаточно велика, чтобы в нем не появлялся бар), и дисперсия $c_r$ в целом сохраняет свой уровень на протяжении десятков оборотов вращения при условии отсутствия релаксационных процессов в вертикальном направлении.

4) Если на начальной стадии эволюции первоначально холодного диска ( $Q_T(r\le 2L)\lee 1$) могут доминировать трехрукавные и даже четырехрукавные моды, то характер спиральной структуры меняется, когда начальное состояние задается субкритическим (неустойчивым, но не очень холодным, для которого $Q_T\gee 1)$. Основной оказывается двухрукавная мода, хотя гармоника $m=3$ также играет важную роль -- особенно на начальных стадиях эволюции. Достаточно характерной особенностью представляется замыкание во внешней области диска спиралей в кольцеобразную структуру. Пространственная структура возмущений в значительной степени зависит также от относительной массы сфероидальной подсистемы.

=0.97

5) В случае очень холодного начального состояния в моделях с маломассивной сфероидальной подсистемой происходит существенное перераспределение вещества в диске и изменение формы кривой вращения $V(r)$ в процессе разогрева и формирования бара. При этом конечное распределение поверхностной плотности $\sigma(r)$ оказывается сильно отличающимся от экспоненциального (рис. 3.5) ^3.8.

Другой особенностью моделей дисков с очень холодным начальным состоянием ($Q_T\lee 1)$ является то, что дисперсия скоростей в конце расчета (через 10-15 оборотов) оказывается несколько больше, чем требуется для гравитационной устойчивости. Причина этого эффекта обусловлена разогревом за счет коллективных процессов -- волновых движений большой амплитуды, возникающих при сильной неустойчивости. Когда диск нагревается и достигает пороговой устойчивости, эти возмущения затухают, однако процесс затухания волн носит инерционный характер: дисперсия скоростей уже обеспечивает устойчивость диска, а спиральные волны еще не затухли (фурье-анализ возмущений плотности диска подтверждает это), и вызывают дополнительный разогрев. Поэтому для получения минимальной дисперсии скоростей, требуемой для устойчивости диска, необходимо использовать итерационный алгоритм последовательных приближений начальной дисперсии скоростей к границе устойчивости [214].

Как и следовало ожидать, граница устойчивости зависит и от первоначальной толщины диска ^3.9. Если диск является изначально толстым (вертикальная шкала $h\gee 0,\!2L$) и неустойчивым лишь в плоскости ( $c_r < c_r^{crit}$), то его разогрев происходит медленнее и прекращается при меньших значениях дисперсии радиальных скоростей, чем в случае изначально тонкого диска. Этот эффект обусловлен двумя факторами: стабилизирующим влиянием конечной толщины диска и медленностью релаксационных процессов в вертикальном направлении по сравнению с характерным временем разогрева в плоскости диска.

Результаты динамического моделирования позволяют определить параметры диска на границе гравитационной устойчивости (когда дисперсия скоростей перестает меняться -- после $5 \div 20$ оборотов диска по внешнему краю).

3.3.3 Граница гравитационной устойчивости. Влияние балджа

Figure: =0.9Параметры диска, проэволюционировавшего к устойчивому состоянию, на границе устойчивости в моделях без балджа: а) для модели, в которой масса гало в пределах $r\le 1 =4L$ равна массе диска и шкала гало $a=L$, показаны радиальные зависимости круговой скорости $V_c(r)$ (линия 1), скорости вращения диска $V(r)$ (линия 2), дисперсии радиальных скоростей $c_r(r)$ (линия 3) и параметров $S$ = $2\Omega /\varkappa$, вычисленных для круговой скорости вращения (линия 4) и скорости вращения диска (линия 5) соответственно; б) параметр Тоомре $Q_T(r)$ на границе устойчивости для серии моделей без балджа с различными параметрами гало. Толстая сплошная линия рассчитана по формуле (3.39)

=0.999

В случае $a\gee L$ кривые вращения имеют протяженный (условно называемый ``твердотельным'') участок роста $V_c(r)$, переходящий в области $r\gee 2L$ в плато $V_c\simeq const$ (линия 1 на рис. 3.16$\!$а). На рис. 3.16$\!$а показаны для модели галактики без балджа с $\mu =1$ радиальные распределения круговой скорости вращения $V_c(r)$ (линия 1), средней скорости вращения частиц $V(r)$ (линия 2), дисперсия радиальных скоростей $c_r(r)$ (линия 3), а также параметры дифференциальности вращения $\Oo S = {2\Omega}/{\varkappa}$ (см. (3.36)), отдельно вычисленные соответственно для скоростей $V_c(r)$ и $V(r)$ (символы 4, 5).

Зная конечные значения дисперсии скоростей, а также плотность диска и скорость вращения, можно для выбранной модели сравнить значения параметра устойчивости Тоомре (3.34) $Q_T$ с аналитически полученными локальными критериями, обсуждавшимися выше в п. 3.3.1, а также последние между собой. Заметим, что аналитические критерии были получены в предположении малости различия между скоростью кругового вращения $V_c(r)$ и средней скоростью вращения $V(r)$ гравитирующих точек. Однако различие между ними для бесстолкновительных дисков может быть существенным. В случае массивного гало ($\mu \gee 2$) различие между параметрами устойчивости, вычисленными для $V_c(r)$ и $V(r)$, мало, но может становиться заметным при $\mu \lee 1$. Это связано с увеличением разности $V_c-V$ с ростом дисперсии скоростей в соответствии с (3.17). Как правило, выполняется условие $S \simeq Q_T^{(M)} \lee Q_T \lee Q_T^{(P)}\!\!$.

Хотя ни один критерий не объясняет модельные зависимости $Q_T(r)$ на всех $r$, ближе всего к ним оказываются критерий ППС, обобщенный на случай конечной толщины по формуле (3.35), и критерий .

Важным результатом представляется то, что радиальная зависимость параметра Тоомре $Q_T(r)$, вычисленная для круговой скорости $V_c(r)$, имеет качественно сходный вид для всех рассмотренных моделей без балджа (рис. 3.16$\!$б). При этом наблюдается примерное постоянство $Q_T(r)$ в области $0\lee r/L\lee 2$ на уровне $Q_T\simeq 1,\!2\div 1,\!6$ (см. рис. 3.16$\!$б). На периферии диска ($r\gee 2L$) с ростом радиуса величина $Q_T$ монотонно увеличивается, достигая на краю диска ($r\simeq 4L$) значений $Q_T\simeq 2,\!5\div 3$. Однако разброс значений $Q_T$ для различных моделей невелик, что позволяет в качестве ограничивающей функции выбрать функцию вида

$$Q_T^{(*)} = A_0+A_1\cdot \left({r\o L}\right) +A_2\cdot \left({r\o L}\right)^2 \,,$$ (3.39)

где $A_0=1,\!25$, $A_1=-0,\!19$, $A_2=0,\!134$ (толстая линия на рис. 3.16$\!$д). Минимум этой функции достигается в точке $r/L=0,\!7$, где он составляет $1,\!2$.

Оценки дисперсии скоростей звездного диска, получаемые из наблюдений, относятся, как правило, к внутренней области диска $r<2L$. Поэтому примерное постоянство $Q_T$ в этой же области является удобным для оценки поверхностной плотности диска и его массы $M_d$ (в предположении его устойчивости), если известна кривая вращения галактики и радиальная экспоненциальная шкала диска $L$. Связывающим соотношением является уравнение

$$c_r = Q_T^{(*)}(r)\, {3,36 G \sigma_0 \exp(-r/L)\o \varkappa} \,,$$ (3.40)

где $Q_T^{(*)}$ для галактик с протяженным участком роста $V_c(r)$ определяется соотношением (3.39). Оценка массы диска $M_d=2\pi \sigma_0 L^2\!$, в свою очередь, при известной скорости вращения позволяет ``вычленить'' маcсу темного гало в пределах данного радиуса.

Рассмотрим теперь модели галактик, у которых кривая вращения в центральной области () определяется прежде всего балджем. Вне балджа $(r\gee L)$ кривые вращения, как правило, являются почти плоскими $V\simeq const$. На рис. 3.17 показаны типичные модельные радиальные зависимости параметров диска для этого случая. При наличии балджа параметр $Q_T$ сильно увеличивается в центральной области диска, где динамика определяется потенциалом балджа. Однако вне этой области в зоне $r\simeq (1\div 2)\cdot L$ радиальная зависимость $Q_T$ сохраняет свой вид (см. (3.39) и рис. 3.16$\!$б). С ростом $r$ величина $Q_T$ монотонно нарастает до значений $2,\!5\div 3,\!5$. Полученное радиальное распределение параметра $Q_T$ является типичным для систем с не очень массивным ( $M_b/M_d \lee 0,\!3$) и не протяженным балджем ( $r_b^{\max} \lee L$).

Figure: Параметры диска на границе устойчивости в моделях с балджем: a) - радиальные зависимости параметров диска (обозначения те же, что на рис. 3.16). Масса гало в пределах $r\le 1 =4L$ равна массе диска, шкала гало $a=3,\!6L$. Параметры балджа: $M_b=0,\!24M_d$, $b=0,\!04L$, $r_b^{\max}=0,\!5L$; б) - параметр Тоомре $Q_T(r)$, рассчитанный с использованием $V_c(r)$, на границе устойчивости для серии моделей с балджем. Толстая сплошная линия построена по формуле (3.39); в) - вид диска с ребра в конце расчета в модели, изображенной на рис. 3.17$\!$а. Точками показаны положения частиц. В центральной области возникает заметное утолщение диска

=0.9996

Чем более массивным и компактным является балдж, тем больше значение $Q_T$ в центре диска. Этот рост параметра Тоомре в основном обусловлен увеличением эпициклической частоты $\varkappa$. С ростом массы сильно концентрированного балджа дисперсия радиальных скоростей в центральной области диска также несколько увеличивается. Заметим, что в модели, показанной на рис. 3.17$\!$а, дополнительный разогрев вблизи центра ($r\lee 0,\!5L$) дисковой подсистемы не связан непосредственно с гравитационной неустойчивостью. В этой модели с $\mu =1$ на начальной стадии формируется бар, который разрушается со временем в результате рассеяния частиц, проходящих вблизи концентрированного ядра, шкала которого $b=0,\!01$. Механизм разрушения бара аналогичен действию массивной черной дыры [463] и более подробно обсуждается в § 3.6.

В результате диск дополнительно нагревается и утолщается в центральной области (см. рис. 3.17$\!$в). Степень дополнительного разогрева и круговая скорость $V_c$ в центре диска очень чувствительны к параметрам балджа -- прежде всего радиусу ядра (в частности, уже при темп указанного разрушения бара сильно замедляется). Поэтому в области $r\lee 0,\!5L$ параметр Тоомре $Q_T$ может очень сильно меняться в разных моделях (см. рис. 3.17$\!$б).

3.3.4 Дифференциальность вращения как фактор,
повышающий порог гравитационной устойчивости

Рассмотрим два предельных случая -- диск, вращение которого близко к твердотельному, и квазикеплеровский диск, скорость вращения которого падает как . Поскольку дифференциальность вращения является дестабилизирующим фактором, для твердотельно вращающегося диска следует ожидать при прочих равных условиях меньшие значения $Q_T$.

Figure: Радиальные зависимости параметров дисков: а) существенная часть диска вращается квазитвердотельно; б) вращение в области $r>L=0,\!25$ близко к кеплеровскому. Система обозначений: 1 -- круговая скорость $V_c(r)$; 2 -- скорость вращения диска (звезд) $V(r)$; 3 -- дисперсия радиальных скоростей $c_r(r)$; 4 -- параметр $S$, рассчитанный по формуле (3.36) для круговой скорости; 6 -- параметр Тоомре $Q_T$, рассчитанный с круговой скоростью; 8 -- критический параметр Тоомре $Q_T^{(P)}$, рассчитанный по критерию (3.37) с $V_c(r)$; 10 -- критический параметр Тоомре $Q_T^{(M)}$, рассчитанный с $V_c(r)$

=0.999

Протяженный участок почти твердотельного вращения в галактике обычно наблюдается в том случае, если масса диска в пределах значительной части диска ($r \lee 2L$) является доминирующей, и, как следствие, для подавления барообразующей неустойчивости требуется более высокий разогрев диска, чем при наличии массивных сферических компонент. Поэтому для выяснения роли дифференциальности вращения рассмотрим модель, где образование бара подавлено массивным гало с ``твердотельным'' участком во внешней области диска ($r\gee L$). Параметр дифференциальности вращения в этой модели $S(r > L)=2\Omega/\varkappa=1,\!1\div 1,\!2$ близок к значению , которое соответствует строго твердотельному вращению (рис. 3.18$\!$а). Радиальные зависимости параметров, характеризующих устойчивость системы $Q_T$, $Q_{T}^{(P)}$, $Q_T^{(M)}$, $S$, приведены на рис. 3.18$\!$а. Как видим, в целом диск оказывается устойчивым при меньших значениях параметра $Q_T$ (кривая $6$) по сравнению со случаями, рассмотренными выше. В центре имеем $Q_T\simeq 1$, а на периферии диска $Q_T\simeq 2$.

Обратимся к другому предельному случаю, который соответствует кривой вращения, близкой к кеплеровской (рис. 3.18$\!$б). У галактик такие участки наблюдаются очень редко [418], однако нас будет интересовать принципиальный вопрос о влиянии сильной дифференциальности вращения на минимально необходимое для устойчивости значение дисперсии скоростей. Для создания квазикеплеровских дисков в динамическую модель вводились массивные концентрированные компоненты. Построенная серия моделей является естественным продолжением моделей с очень массивными балджами $M_b > (2\div 4)\, M_d$. На рис. 3.18$\!$б приведены результаты расчетов для такой модели. Для дисков с сильным дифференциальным вращением значение параметра Тоомре заметно возрастает, так что даже в области, где $Q_T$ минимально ( $r\simeq (1\div 2)\,L$), для устойчивости уже требуется $Q_T > 2$.

3.4 Оценка массы сфероидальных подсистем
для выборки дисковых галактик

3.4.1 Зависимость отношения дисперсии скоростей звезд к скорости
вращения $c_r/V$ от относительной массы гало $\mu = M_h/M_d$

Figure: Результаты декомпозиции кривой вращения галактики NGC 3198 в моделях, которые различаются отношением массы гало к массе диска в пределах $r\le R=4L=10,\!4$ кпк:  а) $\mu=0,\!65$;  б) $\mu =2$;  в) $\mu=5,\!5$. Кривая вращения взята из работы [286], $L=2,\!6$ кпк, $z_{0}=0,\!4$ кпк. Используются распределения плотности в гало (3.3) и диске (3.13). При введении в модель дополнительных компонент (например, балджа) степень неоднозначности декомпозиции еще более усиливается. Модель  а) является моделью максимального диска в случае законов (3.3), (3.13) для NGC 3198

=0.998

Анализ распределения масс в дисковых галактиках базируется на изучении их кривых вращения $V(r)$, определяемых, как правило, по измерению допплеровских скоростей газа. Если максимальная скорость вращения диска позволяет получить грубую оценку массы галактики в пределах определенного радиуса, то форма кривой отражает распределение массы ее основных компонент. Неоднозначность декомпозиции $V(r)$ на составляющие, связанные с отдельными компонентами, заставляет использовать дополнительную информацию о массах и радиальных шкалах компонент, которую дает поверхностная фотометрия диска и балджа. Такой подход мог бы дать полную информацию об относительной массе диска и балджа, однако наличие невидимого компонента (темного гало) априори неизвестной массы и с плохо известным законом распределения плотности значительно усложняет задачу (рис. 3.19). При интерпретации кривой вращения обычно используют метод максимального диска (maximal disk method), нацеленный на определение верхнего предела массы плоского компонента, или метод наилучшего соответствия (best fit method), при котором минимизируется различие между модельной и наблюдаемой формами кривой вращения. Но и в этих случаях результат обычно неоднозначен, и форма кривой вращения может быть объяснена при различных соотношениях между массами дискового и сферического компонента, а следовательно, масса каждого из них может определяться крайне неуверенно.

В последние годы возрастает число галактик, для котоpых известна не только кpивая вpащения, но и диспеpсия скоpостей старых звездных дисков [289, 321, 322, 400, 476, 668]. Анализ дисперсии скоростей позволяет сузить круг возможных моделей галактик, объясняющих наблюдаемую кривую вращения. Основная идея заключается в использовании при моделировании распределения масс в галактиках дополнительного условия, которое можно сформулировать следующим образом: для звездного диска, достигшего стационарного состояния, модельные значения дисперсии скоростей на различных расстояниях от центра должны быть равны или в общем случае не превышать наблюдаемых величин.

Численные эксперименты дают возможность оценить нижний предел массы сферических компонент, при котором исследуемые диски галактик могут находиться в устойчивом состоянии. Если диск обладает маржинальной устойчивостью, то эти оценки должны соответствовать реальной массе компонент.

Возможность таких оценок связана с уменьшением отношения дисперсии скоростей к скорости вращения $c_r/V$ на фиксированном радиусе при увеличении относительной массы сферической подсистемы $\mu=M_s/M_d$ [132]. Эта зависимость следует из простых оценок. В приближении баланса центробежной силы и гравитационной имеем $\Oo V\simeq \sqrt{r\,\frac{\Vert\Phi}{\Vert r}}$ и, отвлекаясь от характера распределения вещества в галактике, по порядку величины примем $\Oo\frac{\Vert\Phi}{\Vert r}\sim G\frac{M_s+M_h}{r^2}$. Для диска на границе гравитационной устойчивости воспользуемся $c_r\propto 1/\varkappa\propto 1/\sqrt{M_s+M_d}$ (см. (3.34)) и в результате имеем зависимость $c_r/V\propto (M_s+M_d)^{-1}\propto (1+\mu)^{-1}$. Данный эффект демонстрирует рис. 3.20, построенный по результатам численного моделирования. Одним из дополнительных доводов в пользу гало является существование вращающихся полярных колец в галактиках [351, 513, 729, 896].

Figure: Зависимость отношения $c_r/V_c$ на радиусе $r=2L$ от относительной массы сфероидальной подсистемы $\mu$ по результатам динамического моделирования. Кружки показывают модели, у которых начальный диск являлся тонким. Модели с начальным толстым диском изображены квадратиком

=0.48

Основная цель расчетов -- выяснить, какими должны быть отношения массы дискового и сферического компонентов для объяснения наблюдаемых скоростей вращения и дисперсии скоростей старых звезд на различных расстояниях от центра. Результатом построения динамической модели являются пространственные распределения различных параметров диска после его выхода на стационарное состояние. Очевидно, что по всему диску должно выполняться условие $c^{mod}\lee c^{obs}$, где $c^{mod}$ и $c^{obs}$ - соответственно экспериментальная (модельная) и наблюдаемая дисперсии скоростей. В областях, где $c^{mod} < c^{obs}$, можно говорить о том, что диск является ``перегретым'', что позволяет пpедположить наличие дополнительных факторов, не учитываемых в модели, которые увеличивают дисперсию радиальных скоростей.

В качестве демонстрации подхода ниже рассмотрим галактику NGC 6503, следуя [207] ^3.10.

3.4.2 Модель галактики NGC 6503

На примере NGC 6503 рассмотрим подробно методику согласования наблюдаемых и модельных радиальных зависимостей скорости вращения и дисперсии. Галактика имеет небольшую экспоненциальную шкалу диска ($L=1,16$ кпк), а оценки дисперсии скоростей звезд относятся к области $r\le 2L$. Кривая вращения галактики $V^{obs}(r)$ взята из работы [287]. Объяснить наблюдаемую $V^{obs}(r)$ можно в рамках моделей с различным соотношением сферической и дисковой подсистем $\mu=M_s/M_d=0,\!8\div 4,\!4$. Массу диска будем оценивать в пределах $4L$.

Радиальная зависимость $c_r(r)$ на границе устойчивости определяется параметрами сферической подсистемы и значением экспоненциальной шкалы диска в соответствии с методикой, описанной в § 3.3. Сравнение с наблюдаемыми значениями дисперсии скоростей требует учета угла наклона диска галактики $i$ к картинной плоскости. С учетом эффектов проекции для дисперсии скоростей вдоль луча зрения имеем

$$c^s = \sqrt{c_z^2 \cos^2(i)+c_\varphi^2\sin^2(i) \cos^2(\alpha) + c_r^2\sin^2(i)\sin^2(\alpha)} \,,$$ (3.41)

где $\alpha$ -- угол между направлением щели и большой осью, измеренной в проекции на плоскость галактики. Следуя [322], примем для NGC 6503 $i=74^\circ$. Щель спектрографа при наблюдениях была ориентирована вдоль большой оси объекта ($\!\alpha=0\!$). Компоненты $c_r, c_\varphi , c_z$ брались из эксперимента.

Figure: Радиальные распределения круговой скорости и дисперсии скоростей по лучу зрения (в км/с) для различных моделей NGC 6503. Данные наблюдений показаны кружками [321]

=0.45

В случае маломассивной сферической подсистемы с $\mu\le 1$ при начальном распределении дисперсии $c_r(r,t=0)$, близком к наблюдаемому, система оказывается неустойчивой, и происходит разогрев диска, в результате которого конечное значение дисперсии скоростей заметно превышает наблюдаемые значения (рис. 3.21). Модель с $\mu=0,\!8$ ($a=0,\!7$) соответствует варианту максимального диска. И при более массивном гало ($\mu =1$, $a=0,\!5$) во внутренней области диска формируется бар, что связано с малой массой и большим значением радиуса ядра гало (``рыхлое гало''), когда в области $r \lee 2L$ масса диска доминирует. В этом случае значение $c_r$ на периферии диска приблизительно в 2 раза превышает наблюдаемые оценки (см. рис. 3.21). В центральной зоне различие не столь велико, но везде выполняется неравенство $c^{mod}>c^{obs}$. В модели максимального диска наблюдаемая кривая круговой скорости вращения наилучшим образом воспроизводится при $M_b=1,\!9\cdot 10^7\,M_\odot$, $M_d=7,\!1\cdot 10^9\,M_\odot$, $M_h=5,\!6\cdot 10^9\,M_\odot$, чему соответствует $\mu=0,\!8$. Наш вывод, что динамическая модель с такими параметрами приводит к сильно нагретому диску ( $c_r/V\simeq 0,\!3$) и противоречит наблюдениям (см. рис. 3.21). Таким образом, несмотря на согласие с кривой вращения, для построения реалистичной модели требуется более массивная сферическая подсистема.

Удовлетворительное согласие между наблюдаемой $V^{gas}(r)$ и модельной $V_c(r)$ можно получить и при более массивных сферических компонентах. Однако динамические модели с очень массивной сферической подсистемой ($\mu \ge 4$) дают дисперсии, для которых везде выполняется $c^{mod} < c^{obs}$. Такая модель совместима с наблюдениями NGC 6503, только если считать, что весь звездный диск галактики существенно перегрет и имеет большой запас гравитационной устойчивости. При этом в кольце $0,\!2 < r/L < 0,\!5$ запас устойчивости по $c_r$ достигает 2 и более раз. Если же исходить из того, что звездный диск близок к границе гравитационной устойчивости, то модели с $\mu \gee 3,\!5$ следует заведомо отбросить. Отсутствие противоречия между результатами динамического моделирования и данными наблюдений имеет место при $\mu=1,\!6\div 3,\!5$. Из рассмотренных моделей наиболее предпочтительными представляются модели с $\mu=1,\!62$ и $\mu=2,\!38$ (см. рис. 3.21), дающие наилучшее согласие с наблюдениями. Это позволяет сделать вывод, что масса сферической подсистемы в галактике NGC 6503 превышает массу диска как минимум в 1,6 раза. Вклад балджа в массу сферической составляющей остается пренебрежительно малым.

Вывод о сравнительно небольшой массе диска NGC 6503 cогласуется с результатами pаботы [322] по моделированию этой галактики.

3.4.3 Оценка массы маржинально устойчивых дисков

Table: Параметры галактик по данным наблюдений

1	2	3	4	5	6	7	8	9
Галактика	Тип	$D$ (Мпк)	$i^\circ$	$c_{obs}$ (км/с)		$V_c(2L)$	$L^{''}$
NGC1068	3	15,2	30	$50\pm 10$	[792]	251	55,6	[264]
NGC2460	1	19,2	46	$60\pm 10$	[792]	200	15,0	[792]
NGC2775	2	18,0	40		[792]	283	3,05	[792]
NGC4030	2	19,5	40	$55\pm 10$	[792]	249	18,0	[792]
NGC3982	3	15,8	30,4	$45\pm 10$	[292]	200	10,2	[264]
NGC1566	4	17,5	28	$20\pm 10$	[321]	181	35,7	[321]
NGC2613	3	19,2	90	$36\pm 25$	[321]	300	57,3	[264, 321]
NGC3198	5	12,2	70	$20\pm 15$	[321]	180	58,0	[321]
NGC5247	4	15,3	43	$20\pm 10$	[321]	83	40,0	[321]
NGC6340	0	19,1	26	$35\pm 15$	[321]	163	28,0	[321]
NGC6503	6	5,9	71	$18\pm 10$	[321]	112	40,0	[321]
IC750	2	12,9	71	$70\pm 30$	[476]	170	14,2	[264]
NGC470	3	33,9	60	$40\pm 20$	[289]	185	13,6	[455]
NGC4419	1	14,0	71	$60\pm 20$	[289]	148	12,8	[264]
NGC7782	3	74,6	58	$45\pm 15$	[289]	295	18,3	[264]
NGC2962	-1	24,1	59	$60\pm 20$	[808]	209	22,3	[264]
NGC3630	-1	17,4	90	$80\pm 20$	[808]	186	8,3	[264]
NGC4143	-2	12,7	60		[809]	235	15,4	[264]
NGC4203	-3	14,3	55	$50\pm 20$	[809]	92	17,2	[264]
NGC4578	-2	14,0	50		[809]	136	10,3	[264]
NGC5273	-2	15,1	44	$50\pm 15$	[809]	105	9,2	[264]
NGC584	-4	25,5	90	$80\pm 40$	[668]	215	8,5	[668]
NGC2549	-2	15,8	90	$50\pm 20$	[668]	153	20,2	[668]
NGC2768	-4	20,4	90	$73\pm 20$	[668]	138	44,8	[668]
NGC3489	-1	10,8	60	$78\pm 22$	[668]	137	19,4	[668]
NGC4251	-2	13,5	68		[668]	135	22,6	[668]
NGC4649	-4	14,0	49		[668]	227	29,6	[668]
NGC4753	-2	16,3	71	$50\pm 25$	[668]	185	34,8	[668]
NGC5866	-1	11,9	75	$100\pm 20$	[668]	217	21,0	[668]

Примечание. (1) - Обозначение галактики. (2) - Морфологический тип (по базе данных LEDA) в обозначениях Вокулера. Принято относить $T = -1, 1, 3, 5, 7$ к галактикам $SO, Sa, Sb, Sc, Sd$ соответственно. (3) - Принятые расстояния $D$ до галактик. Для галактик с лучевой скоростью $V_r > 800$ км/с расстояния соответствуют постоянной Хаббла $H_0 = 75$ км/с/Мпк (кроме галактик скопления Virgo, для которого принималось  Мпк). Для близких галактик с меньшей лучевой скоростью (NGC 3198, NGC 6503, IC 750) использовался модуль расстояния, приведенный в LEDA. (4) - Угол наклона диска $i$. Его значения брались по LEDA, за исключением NGC 1566, где сильно отличающаяся оценка $i$ ( вместо $44^\circ$) приведена в работе [Bottema R.//. 1992. V. 257. P. 69.], и тех галактик, для которых непосредственно оценивались радиальные дисперсии скоростей [792] (для них сохранены значения $i$ по цитируемой работе). (5, 6) - Наблюдаемые значения дисперсии скоростей на $r \simeq 2L$ (вдоль большой оси) и соответствующий литературный источник. Ошибки значений, если они не приведены в оригинальной работе, определялись визуально по разбросу точек на графике, и являются лишь грубой оценкой точности. (7) - Принимаемые значения круговой скорости вращения $V_c$ на $r \simeq 2L$ (для кривых вращения звездной компоненты данные исправлены за дисперсию скоростей звезд). Для NGC 5247 значение $V_c(2L)$ принято равным максимальной скорости вращения $V_m$ по ширине радиолинии HI (по LEDA). (8, 9) - Фотометрическая шкала диска (в угловых секундах) и соответствующий литературный источник.

В рамках предположения маржинальной устойчивости старых звездных дисков оценим массы дисков $M_d$ в пределах $r=4L$, основываясь на формуле (3.39), которую перепишем:

$$c_r = \frac{3,\!36\, G \sigma}{\varkappa}\,Q^{(*)}_T \,.$$ (3.42)

Рассмотрим галактики, для которых имеются оценки дисперсии скоростей звезд на достаточно большом расстоянии от центра в области $(1,5-2)\cdot L$ ($L$ -- фотометрическая шкала диска). В этом случае $Q^{(*)}_T\gee 1,5$ и мы в максимальной степени освобождаемся от влияния балджа. В [65] построена выборка с известными из наблюдений оценками дисперсии скоростей звезд вдоль луча зрения на таких расстояниях от центра, которая состоит из 29 объектов (табл. 3.1).

Учитывая, что $\sigma(2L) = {k\, c_r\, V_c}/{7,72 L G Q^{(*)}_T}$, запишем выражение для поверхностной плотности диска на радиусе $r=2L$ в удобной форме:

$$\sigma (2L)[M_\odot/\textrm{пк}^2] = 6,9\cdot 10^{-2}\, \f... ...}]\, V_c [\textrm{км/с}]}{2Q^{(*)}_T\,L\,[\textrm{кпк}]} \,,$$ (3.43)

где значения параметра $k = \varkappa/\Omega$ лежат в пределах от 2 в случае твердотельного вращения до $\sqrt 2$ для плато на кривой вращения, а $V_c$ и относятся к радиальной координате $r=2L$. В результате вычисляем массу диска с экспоненциальным профилем плотности $M_d = 2\pi L^2\, \sigma(2L)\, e^2$. Переход от $c^{obs}$ к $c_r$ определяется (3.41).

Figure: Сопоставление отношения $c_r/V_c$ с морфологическим типом (a) и интегральным показателем цвета галактики (б)

=0.33

Обсудим некоторые результаты, следующие из определения величин $M_d$, $\sigma (2L)$ [65]. Роль вращения в равновесии диска удобно характеризовать отношением радиальной дисперсии скоростей к скорости кругового вращения. На рис. 3.22$\!$а,$\!$б отношение $c_r/V_c$ сравнивается с морфологическим типом $T$ и с показателем цвета $(B-V)_0$. Здесь отчетливо прослеживается взаимосвязь сравниваемых величин. Зависимость $c_r/V_c$ от $T$ (рис. 3.22$\!$а) указывает на то, что в галактиках поздних типов вращение играет более важную роль в поддержании равновесия старого звездного диска, чем в галактиках $Sa$ - $SO$.

Из рис. 3.22$\!$б следует, что динамически ``холодные'' диски отличаются более интенсивным звездообразованием, о чем свидетельствует их более голубой цвет. С другой стороны, ``красные'' галактики (среди них преобладают $Sa$ - $SO$) обладают большей дисперсией кинематических свойств, и среди них довольно много сильно ``перегретых'' систем c высоким отношением $c_r/V_c$. Граница между ``холодными'' и ``горячими'' дисками соответствует значению $(B-V)_0 \simeq 0,75$.

Figure: Сопоставление локальных плотностей диска на $r \simeq 2L$, вычисленных в предположении его маржинальной устойчивости, с интегральными показателями цвета галактик. Выделяется группа ``красных’’ галактик, для которых оценки $\sigma (2L)$, по-видимому, сильно завышены

=0.6

На рис. 3.23 приведены значения локальных плотностей диска на выбранном расстоянии от центра, вычисленные по (3.43), которые сопоставлены с интегральным показателем цвета галактики. Отчетливо выделяется группа ``красных'' галактик (почти все они относятся к типу $SO$) с аномально высокими значениями критической плотности диска, превышающими $\!400\,M_\odot /$пк, в то время как для большинства остальных галактик $\!\sigma(2L)\!$ находится в пределах 50–200 $\!M_\odot /$пк. Для сравнения: диск нашей Галактики в окрестности Солнца имеет плотность, не превышающую 60 $\!M_\odot /$пк (§ 3.6, [213]). Это позволяет предположить, что у части галактик наблюдаемая дисперсия скоростей звезд существенно превосходит минимальное значение, требуемое для устойчивости диска.

Figure: Сравнение отношения массы маржинально устойчивого диска к полной массе галактики $M_d / M_t$ в пределах $r=4L$ с морфологическим типом (а) и интегральным показателем цвета галактики (б)

=0.33

Сходная картина наблюдается и при сопоставлении относительной массы диска, вычисляемой в предположении его маржинальной устойчивости, с морфологическим типом и показателем цвета галактик (рис. 3.24$\!$а,$\!$б). В общем случае $M_d$ является верхним пределом массы диска, поскольку дисперсия скоростей звезд в диске галактики может превышать минимальное значение, требуемое для его устойчивости. Горизонтальная линия отделяет объекты с отношением $M_d/M_t>1$. Последнее неравенство не имеет физического смысла и говорит лишь о том, что для этих галактик предположение о маржинальной устойчивости диска не согласуется с принятым значением $c_r\!$. Либо такие галактики обладают сильно ``нагретыми’’ (с большим запасом устойчивости) дисками, либо на оценку $c_r$ повлияли звезды балджа, более ``горячего'', чем диск. Допустимы оба варианта, и для каждой галактики вопрос должен решаться отдельно. Отметим, однако, что на радиальном профиле $c_{obs}(r)$ внутренние части галактики, где преобладает балдж, как правило, заметно отличаются от прилегающих областей диска, где дисперсия скоростей ниже и медленно падает с $r$ (см.  например, [808, 809]). В рассматриваемых галактиках с $M_d / M_t$ > 1 (кроме NGC 3489) область $r \simeq 2L$ приходится на ``дисковый'' участок $c_{obs}(r)$ или на переходную область, что является косвенным аргументом в пользу того, что наблюдаемая дисперсия скоростей, по крайней мере в части из них, не сильно искажена влиянием балджа.

Для некоторых галактик можно проверить, является ли оценка $M_d / M_t$ > 1 результатом завышения $c_{obs}(2L)$, используя уже имеющиеся измерения. Для трех линзовидных галактик с $M_d/M_t>1$ (NGC 4251, NGC 4578 и NGC 5273) оценки дисперсии скоростей получены вплоть до значений $r/L = 3,\!6; 3,\!3$ и соответственно, то есть до расстояний, где влияние балджа должно быть существенно меньше, чем на . Хотя на больших $r$ возрастает неопределенность в значении параметра $Q_T^{(*)}$, мы можем принять, что для этих предельных расстояний продолжает выполняться условие , и оценить таким образом нижний предел $M_d$. Оказалось, что и в этом случае для отношения $M_d / M_t$ перечисленных галактик получаются превышающими единицу (1,3; 2,0 и 1,2 соответственно), то есть вывод о ``перегретости'' их дисков сохраняется.

Со спиральными галактиками ситуация иная. Для большинства из них выполняется условие $M_d/M_t< 1$, однако из его выполнения еще не следует, что дисперсия скоростей в их дисках близка к минимальному значению для гравитационной устойчивости. Здесь требуются независимые оценки масс дисков.

Figure: Связь отношения массы маржинально устойчивого диска к интегральной светимости галактики с интегральным показателем цвета галактики. Кривая линия -- зависимость $\lg M_d/L_B=1,\!937(B-V)_0 - 1,\!019$, полученная методом эволюционного моделирования звездных систем (см. Табл. A3 для модели ``closed box'' в работе [288])

=0.55

Для сравнения $M_d$ со значениями, ожидаемыми для данной светимости галактики, на рис. 3.25 приведена диаграмма $M_d/L_B$ -- показатель цвета для спиральных галактик рассматриваемой выборки. Очевидно, что отношение $M_d/L_B$ для звездного населения (обычно составляющее несколько солнечных единиц) возрастает по мере уменьшения вклада молодых звезд в интегральную светимость, то есть с ростом показателя цвета. Несмотря на значительную дисперсию точек на рис. 3.25 относительно модельной кривой, можно говорить о количественном согласии полученных оценок масс дисков, отвечающих условию маржинальной устойчивости, с ожидаемыми для данного цвета и светимости. Это является веским аргументом в пользу того, что дисперсия скоростей звезд в дисках спиральных галактик в большинстве случаев близка к минимальному значению, требуемому для их устойчивости. Отсюда следует, что механизмы медленного динамического ``нагрева'' стационарных дисков в рассмотренных спиральных галактиках недостаточно эффективны, чтобы привести к существенному возрастанию дисперсии скоростей за время их существования.

Таким образом, звездные диски в галактиках ранних типов, по-видимому, часто оказываются сильно ``перегретыми''. В первую очередь это следует из неприемлемо высоких оценок локальных плотностей и интегральных масс дисков, которые получаются в предположении их маржинальной устойчивости. При этом явно прослеживается связь высокой дисперсии скоростей с низким темпом звездообразования. Действительно, относительная величина дисперсии скоростей $c_r/V$ систематически возрастает с показателем цвета галактики (рис. 3.22$\!$б), причем все галактики с $M_d/M_t>1$ имеют цвет старого звездного населения ( $(B-V)_0 >0,75$).

3.4.4 Оценка массы гало для галактик позднего типа

Протяженная радиальная зависимость дисперсии скоростей звезд в диске известна для небольшого числа объектов. Поэтому представляет интерес оценка массы гало только по наблюдаемой центральной дисперсии скоростей $c^{obs}$. Это в принципе возможно, если галактика не имеет балджа, тогда $c^{obs}$ можно относить к дисковой компоненте. Для этой цели могут подходить галактики позднего типа ($Sc$, $Sd$, $Sm$).

В основе рассмотрения [210] лежит полученная c помощью динамического моделирования зависимость отношения дисперсии радиальных скоростей $c_r(r=0)$ к максимальной скорости вращения $\beta \equiv c_r(0)/V^{(m)}$ от относительной массы гало $\mu = M_h/M_d$.

Кривые вращения галактик без больших балджей, как правило, демонстрируют протяженный участок монотонного роста скорости вращения в области $r \lee 2L$, который хорошо объясняется экспоненциальным законом распределения вещества в диске, если выполняется $a\gee L$. Другой особенностью кривых вращения является протяженное плато в области $r\gee 2L$, которое часто прослеживается существенно дальше оптического радиуса.

Figure: Радиальные зависимости круговой скорости вращения $V_c$ и дисперсии радиальных скоростей $c_r$ при различных $\mu$ и $a=L$ по результатам динамического моделирования: для $\mu =1$ зависимость 1 - $V_c$, кривая 2 - $c_r$; для $\mu =3$ кривая 3 - $V_c$, 4 - $c_r$; для $\mu =4$ зависимость 5 - $V_c$, 6 - $c_r$

=0.55

С ростом вклада гало в массу галактики имеем уменьшение отношения дисперсии скоростей звезд к скорости их вращения $V$ (см. рис. 3.20). Аналогичный эффект имеет место для центральной области (рис. 3.26). На рис. 3.27 показана зависимость $\beta(\mu)$ по результатам динамического моделирования. Скорость вращения звезд $V$ меньше круговой скорости $V_c$, и эта разница заметно увеличивается в случае маломассивного гало (см. рис. 3.27). Поэтому для сравнения с наблюдательными данными более предпочтительной является зависимость $\beta(\mu)$, вычисленная с использованием круговой скорости вращения.

Figure: Отношение дисперсии радиальных скоростей звезд в центре диска $c_r(0)$ к максимальной круговой скорости $V_c^{(m)}$ (кривая 1) и максимальной скорости вращения звезд $V^{(m)}$ (кривая 2) при различных относительных массах гало $\mu = M_h/M_d$ с $a=L$ по результатам динамического моделирования диска без учета балджа. Кривые 3 и 4 построены соответственно для моделей с $a=2L$ и $a=3L$

=0.45

Функция $\beta(\mu)$ зависит от шкалы гало $a$ (см. рис. 3.27). При постоянном $\mu$ с ростом значения $a$ отношение $c_r(0)/V_c^{(m)}$ увеличивается. Поэтому, если для оценки параметра $\mu$ по известному значению $\beta$ пользоваться кривой 1 на рис. 3.27 (случай $a=L$), то результатом будет являться оценка массы гало снизу. Зависимости $\beta(\mu)$ в случае $a>L$ дают большие значения $\mu$, тем самым уменьшая массу диска.

При сравнении с наблюдательными данными, поскольку дисперсия скоростей звезд в балдже больше, чем в диске, будем получать нижнюю границу относительной массы гало $\mu$.

Считаем, что максимальная круговая скорость вращения $V_c^{(m)}$ равна максимальной скорости вращения газа, измеренной либо в оптике $V^{(m)}_{opt}$ ($H_\alpha$), либо по радионаблюдениям $V^{(m)}_{rad}$ ($HI$) -- эти значения предоставляет электронный каталог LEDA. В дополнение каталог дает приведенную к одной системе максимальную скорость вращения $V^{(m)}_{rot}$ и удвоенную скорость вращения без исправления за наклон галактики $\Delta V^{(m)}$. Полученное из наблюдательных данных значение параметра $\beta$ позволяет с помощью зависимости 1 на рис. 3.27 оценить относительную массу гало [210]. Из рассмотрения необходимо исключить галактики с $\beta > 0,9$, поскольку для таких объектов заведомо неприменима зависимость, изображенная на рис. 3.27. Причина больших значений $\beta$ может быть связана с заметным балджем, как например, у NGC 628, 4254, 4536, 5480 [264], что не позволяет для этих объектов оценить массу гало только по центральной дисперсии скоростей. На рис. 3.28 показаны распределения числа галактик по относительным массам гало $\mu$ [210]. Вычисление средних значений дало: $\langle c_r(0)/V^{(m)}_{rad}\rangle \,=0,\!54$; $\langle c_r(0)/V^{(m)}_{opt}\rangle\,=0,\!55$; $\langle c_r(0)/V^{(m)}_{rot}\rangle \,=0,\!56$ что приводит к средней относительной массе гало $\langle \mu\rangle \simeq 0,\!8$.

Figure: Распределения числа галактик позднего типа ($t\ge 4$) по относительным массам гало $\mu$, вычисленные c использованием: a) $V^{(m)}_{rad}$; б) $V^{(m)}_{opt}$; в) $V^{(m)}_{rot}$

=0.999

Такой подход позволяет выделить галактики с малым $\beta$ (например, NGC 598, 1353, 2998, 3198, 3938, 4565, 7171, 7217, 7541), которые могут обладать достаточно массивным гало, превышающим массу диска в два и более раза, и такие объекты требуют особого рассмотрения.

3.5 Изгибные неустойчивости звездного диска

3.5.1 Вертикальная структура звездных дисков
и изгибные неустойчивости

Другая возможность оценки массы гало связана с использованием при построении динамических моделей наблюдаемой толщины звездного диска (зависящей от дисперсии вертикальных скоростей). В основе такого подхода лежит зависимость вертикальной шкалы диска (при данной дисперсии скоростей) от локальной поверхностной плотности диска и от массы сфероидальной подсистемы $M_s$, что впервые было показано в работе [53] (см. также [627, 847]).

Вопрос о механизмах увеличения дисперсии случайных скоростей звезд $c_z$ от $6\div 10$ км/с у молодых звезд до значений $\sim 30\div 100$ км/с у старого населения остается одним из фундаментальных в физике галактик [714]. Помимо механизмов вертикального нагрева, связанных с рассеянием звезд на гигантских молекулярных облаках [827, 828] и на спиральных волнах плотности [517], важным является возможность роста дисперсии $c_z$ из-за неустойчивости изгибных возмущений в диске. В случае спиральной волны на это указывает анализ поля скоростей в NGC 3631 [199], где впервые было показано наличие вертикальных движений, связанных со спиральной волной. Оценки отношения $c_z/c_r$ с использованием данных наблюдений различных галактик дают $c_z/c_r \simeq 0,4-0,8$, но более типичные значения $0,5\div 0,7$ [559].

По-видимому, доминирующий механизм вертикального разогрева у звездных дисков может изменяться в разные эпохи. Согласуя данные наблюдений с результатами динамического моделирования галактики, можно получить оценку на массу гало, которая является нижней границей, поскольку существуют и другие механизмы нагрева диска, не учитываемые в численной модели. В рамках моделей $N\!$-тел рассматривались различные аспекты изгибов звездных галактических дисков. Важные результаты получены в моделях с учетом приливных взаимодействий [481, 614, 875, 890]. Спутники рождают изгибы и утолщают диск, что следует из сравнения данных наблюдений изгибов у одиночных галактик и в группах [727]. Было показано формирование в центральной области диска с ребра ящекообразных структур в результате изгибной неустойчивости [698, 786]. Условия возникновения изгибных мод исследовались в работах [187, 299, 454, 725, 787]. Изгибная неустойчивость может развиваться значительно медленнее по сравнению с гравитационной неустойчивостью в плоскости диска так, что характерные времена насыщения составляют порядка миллиарда лет и больше [187]. Влияние балджа изучалось в [825].

В первую очередь рассмотрим вопрос о радиальном распределении отношения $c_z/c_r$ и вертикальной шкалы диска, которые минимально обеспечивают устойчивость относительно различных изгибных возмущений. Поскольку для галактик, видимых с ребра, скорость вращения в центральной области измеряется неуверенно (см. § 2.6), будем рассматривать только галактики поздних типов, у которых отсутствует яркий балдж. Это позволяет восстановить внутреннюю часть кривой вращения, даже если она плохо определена из наблюдений, считая, что форма кривой круговой скорости галактики в центральной области ($r \lee 2L$) определяется, главным образом, дисковой компонентой. Кроме того, наличие балджа при прочих равных условиях играет стабилизирующую роль для изгибной неустойчивости, ослабляя зависимость относительной толщины диска $h/L$ от относительной массы гало $M_h /M_d$ [825].

В [307, 847] построены динамические модели для 7 галактик (в частности, UGC 6080, UGC 9556, UGC 9422, NGC 4738), видимых с ребра, с известными фотометрическими шкалами распределения яркости в $r$ и $z$ направлениях. Особый интерес представляет определение параметров подсистем для супертонкой галактики UGC 7321. Кроме перечисленных, рассмотрены галактики NGC 5170 и NGC 891, для которых, помимо радиальной и вертикальной шкалы, известны и радиальные зависимости дисперсии скоростей звезд, что позволяет производить оценку масс компонентов для них двумя независимыми способами -- сравнивая результаты моделирования с наблюдаемыми дисперсией скоростей звезд и толщиной диска.

Наблюдаемое отношение радиальной шкалы распределения яркости и (в предположении постоянства вдоль радиуса отношения массы к светимости) плотности дисков галактик к вертикальной шкале лежит в достаточно широких пределах $L/z_0=2\div 12$ [320, 452, 453, 560, 561, 562]. Такой большой разброс значений может означать, что относительная масса гало $\mu$ внутри оптического радиуса тоже сильно меняется от галактики к галактике.

Принято принимать для всего старого звездного диска отношение $c_z/c_r = {\rm const}$ [321, 323]. Этот вывод является весьма приближенным, и динамическое моделирование показывает, что $c_z/c_r$ меняется с радиусом (п. 3.5.2). Вертикальная шкала звездных дисков зависит от дисперсии вертикальных скоростей $c_z(r)$ (см. п. 3.1.2), при этом сама $c_z$ не является независимой от дисперсии радиальных скоростей.

По-видимому, впервые вопрос об отношении дисперсии вертикальных скоростей звезд $c_z$ к дисперсии радиальных скоростей $c_r$ был рассмотрен Toomre [852]. Динамика изгибных (мембранных) колебаний в моделях холодных тонких дисков изучена в работе Хантера и Тоомре [501]. Это исследование имело целью объяснение наблюдаемого в ряде изолированных галактик крупномасштабного искривления периферии их дисков. Другой проблемой, для решения которой необходимо изучение динамики изгибных возмущений, является задача объяснения существенного различия толщин и $z$-дисперсий скоростей объектов звездного и газового дисков. В работах [566, 605] было показано, что для решения упомянутых выше проблем необходимо изучать динамику изгибных возмущений в моделях дисков, горячих в их плоскости.

=0.95

Поляченко и Шухман [172] в рамках простой модели однородного тонкого самогравитирующего слоя получили, что для стабилизации относительно мелкомасштабных изгибных возмущений должно выполняться условие $\alpha_z \equiv c_z/c_r \ge 0,\!37$. Стабилизация изгибных волн достигается при определенной величине $c_z$, которой соответствует минимальная толщина устойчивого диска. Араки [250] рассмотрел динамику изгибных возмущений с учетом неоднородного распределения объемной плотности вдоль $z$-координаты. Вывод о малом критическом значении $c_z/c_r \gee 0,\!3$ сохранился (см. обсуждение в работе [621]).

3.5.2 Численное моделирование изгибных неустойчивостей

Крупномасштабная осесимметричная изгибная неустойчивость. В первую очередь обсудим нелинейную динамику наиболее крупномасштабных изгибных возмущений. Линейный анализ устойчивости глобальных изгибных возмущений проведен в работе [173] (более общий случай рассмотрен в [868]). В модели двухосного твердотельно вращающегося звездного эллипсоида однородной плотности было показано, что наиболее крупномасштабные моды с азимутальными числами $m=0, 1, 2$ могут быть неустойчивы, и исследовано влияние на границы устойчивости отношения полуосей эллипсоида, параметра $\mu = M_h/M_d$, дисперсии скоростей в плоскости системы. В целом наиболее важным результатом является обнаружение зависимости положения границ областей неустойчивости от массы гало: при достаточно большой массе гало неустойчивыми могут стать системы с малой дисперсией скоростей в плоскости эллипсоида. В этом состоит дестабилизирующая роль гало.

Однако, поскольку с ростом $M_h /M_d$ необходимое для гравитационной устойчивости диска отношение дисперсии скоростей звезд в его плоскости к максимальной скорости вращения $c_r/V^{\max}$ убывает (см. п. 3.4.1), то, во всяком случае на границе устойчивости, дестабилизирующая (по отношению к крупномасштабным изгибным возмущениям) роль массивного гало не проявляется.

Почему встречаются тонкие звездные диски? Значения полутолщины звездного диска лежат в широких пределах $\Delta = 0,\!1 \div 1$ кпк. Причем достаточно многочисленны наблюдаемые с ребра галактики с отношением видимых полуосей $\chi = b/a \le 0,\!1$. Относительную толщину звездного диска естественно определить отношением . В случае распределения объемной плотности можно принять $\chi /\chi_0 > 0,\!5$ [53]. Тем самым для тонких звездных дисков ( $\chi \le 0,\!1$) считаем $\chi_0 < 0,\!2$. Обсудим условия, при которых стационарные звездные диски могут иметь такую толщину.

Стационарная система должна быть, во-первых, гравитационно устойчива относительно возмущений, лежащих в плоскости диска, что накладывает ограничения на дисперсию радиальных скоростей $c_r \ge Q\,c_T$. Во-вторых, устойчивость относительно мелкомасштабных изгибных возмущений требует выполнения условия (п. 2.5.2) $\alpha^{-1} = c_z/c_r \ge \alpha^{-1}_{crit} \simeq 0,\!4$. В свою очередь, полутолщина диска $\Delta$ зависит от величины $c_z$. Считая, что система находится на границе устойчивости, получаем

$$\Delta = \left({Q \o \alpha_{crit}}\right)^2{3,\!6\,G\,\s_{*0}(r) \o \varkappa^2}\,.$$ (3.44)

Круговая скорость $V_{\textrm{вр}}$ в диске определяется распределением вещества в плоской и сферической подсистемах, поэтому запишем

$$V^2_{\textrm{вр}} = V^2_d + V^2_h \,. %\eqno(3.4.13)$$ (3.45)

Для экспоненциального профиля плотности (1.2) масса диска $M_d~= 2\,\pi\,\s_{*0}(0)\cdot L^2_\s$, и в области $r \,\gee\, 2\,L_\s$ скорость вращения близка к своему максимальному значению $V^2_d = 0,\!388\,G\, M_d/L_\s$. Примем, что $V^2_h~= G\,M_h / 4\,L_\s$ (масса гало $M_h$ находится внутри $r = 4\,L_\s$). В результате для скорости вращения имеем

Для плоской кривой вращения и для относительной толщины диска можем записать [53]

где $\mu = M_h/M_d$, $K = 0,\!74$. Прежде всего заметим, что для $Q/\alpha_{crit} ={\rm const}$ параметр в области $1 \lee r/L_\s \lee 4$ слабо зависит от радиуса, что не противоречит наблюдениям. Из (3.47) видно, что с увеличением массы гало полутолщина звездного диска уменьшается. Для уточнения данного соотношения обратимся к результатам численных экспериментов.

Figure: Зависимость от времени параметров диска в процессе развития осесимметричной изгибной моды в диске в модели с $\mu =1$, $a=L$: а) - вертикальная координата центра тяжести вещества диска $\zeta$; б) - дисперсия вертикальных скоростей частиц $c_z$; в) - вертикальная шкала диска $z_0$; г) - отношение $c_z$ к дисперсии радиальных скоростей $c_r$; д) - $c_r$; е) - скорость вращения частиц диска $V\!$. Разные кривые даны для различных радиусов $r_j$, числа указывают значение параметра $j$, который определяет расстояние до центра диска: $r_j = (0,025+(j-1)\cdot 0,05)\cdot 4L$. Все параметры усреднены по азимутальному углу

=0.999

Эволюция системы с малым начальным отношением $\alpha _z=c_z/c_r$ (холодные в вертикальном направлении) наглядно демонстрирует нарастание со временем крупномасштабных изгибных возмущений, которые приводят к вертикальному разогреву и, как следствие, утолщению диска. Особенно сильный разогрев диска в вертикальном направлении, приводящий к значительному утолщению диска, получается в процессе развития неустойчивой осесимметричной изгибной моды ($m=0$). Осесимметричная мода является наиболее важным феноменом изгибной неустойчивости. На рис. 3.29 показаны зависимости от времени вертикальной координаты центра тяжести вещества , дисперсии вертикальных скоростей , вертикальной шкалы диска $z_0(r,t)$, отношения дисперсий скоростей $\alpha_z\equiv c_z(r,t)/c_r(r,t)$, дисперсии радиальных скоростей $c_r(r,t)$, скорости вращения частиц в диске $V(r,t)$.

На протяжении приблизительно 2,5 оборотов вращения ($t\sim 10$) по внешнему краю диска его параметры почти не меняются (см. рис. 3.29), происходит формирование собственных мод на линейной стадии развития изгибной неустойчивости. После начинается нелинейная стадия развития изгибной неустойчивости, и амплитуда смещения центра тяжести в $z$-направлении возрастает (рис. 3.29$\!$а). В центральной зоне диска (линии 1-5) амплитуда вертикального смещения быстрее достигает максимального значения, уменьшаясь затем до исходного уровня (см. рис. 3.29$\!$а). На периферии диска (линии 11-19) изменение $\zeta$ происходит заметно медленнее.

Несколько позже, с отставанием от величины , начинается резкое увеличение дисперсии $z$-скоростей $c_z$ (рис. 3.29$\!$б) и вертикальной шкалы диска $z_0$ (рис. 3.29$\!$в). Утолщение системы, что выражается в росте $z_0$, в данной модели начинается в центральной области, быстро захватывая весь диск. Величина $\alpha _z$ заметно увеличивается за счет роста $c_z$ и небольшого уменьшения $c_r$ (рис. 3.29$\!$г,$\!$д). Аналогичное поведение обнаруживает дисперсия азимутальной компоненты скорости $c_\varphi$, для которой выполняется приближенное равенство $c_\varphi\simeq c_r \varkappa/2\Omega$ ^3.11.

Уменьшение $c_r$ и $c_\varphi$ обусловлено переходом кинетической энергии случайного движения в плоскости диска в кинетическую энергию вертикального движения. Подчеркнем, что развитие данной изгибной моды происходит на фоне осесимметричного по всем параметрам диска.

Figure: Форма диска в процессе развития изгибной неустойчивости в момент времени $t=25,4$ для расчета, изображенного на рис. 3.29. Показаны изолинии распределения смещения центра тяжести диска в вертикальном направлении $\zeta (r,\varphi )$ в плоскости диска (а); функция $\zeta (x,y)$ (б). Жирная линия соответствует значению $\zeta =0$ (в). Для этого же момента времени даны изолинии распределения логарифма поверхностной плотности, которые демонстрируют наличие осевой симметрии

=0.999

Величина $\zeta$ имеет разные знаки в центре и на периферии диска (см. рис. 3.29$\!$а), поэтому при развитии неустойчивости формируется структура типа ``купола'' (рис. 3.30). Изолинии параметра $\zeta$ близки к окружностям (см. рис. 3.30$\!$а). К моменту времени $t=25,\!4=6T_0$ внутреннее кольцо и периферия диска смещены в противоположные стороны, а центральная область ($r\lee 0,4$) уже вернулась в исходное состояние (рис. 3.30$\!$б). Распределение параметра $\zeta$ в плоскости диска имеет вид ``сомбреро''.

Figure: Изображение диска с ребра на стадии глобальной осесимметричной изгибной моды в модели с $\mu =4$. В вертикальном направлении масштаб в 4 раза больше, чем в горизонтальном

=0.6

Структура диска на стадии развития изгибной моды $m=0$, видимого с ребра, изображена на рис. 3.31. Имеем характерный ``ящекообразный'' вид, который типичен для всех моделей на этапе доминирования осесимметричной изгибной моды. Следует особо подчеркнуть, что характерная ``ящекообразная'' структура не связана с баром, как принято объяснять данные наблюдений в ряде случаев [328, 785].

Эволюция дисперсий скоростей $c_z$, $c_r$ и скорости вращения звездного диска $V$ начинаются после того, как амплитуда вертикального смещения $\zeta$ оказывается значительной. Вертикальный разогрев диска характеризуется ростом отношения $c_z/c_r$, но, начиная с некоторых значений $c_z/c_r$, условия для развития изгибной неустойчивости исчезают. В результате система приходит в новое стационарное состояние с более толстым диском. Характерные времена этого процесса сильно зависят от параметров модели и с учетом линейной стадии могут составлять десятки оборотов по внешнему краю звездного диска. Если распределение $\alpha_z(r)$ является субкритическим, то из-за малости инкрементов неустойчивости линейная стадия увеличивается, и разогрев на нелинейном этапе оказывается слабым. Таким образом, амплитуда изгибной моды и сама возможность ее развития зависят в первую очередь от начального радиального распределения $c_z/c_r$.

Очень важным представляется вывод о том, что конечное распределение параметра $\alpha_z(r)$, которое получается в результате развития глобальной изгибной неустойчивости, зависит от начальной функции $\alpha_z(r,t=0)$. Модели с маленькой начальной вертикальной шкалой (тонкие диски), разогреваясь вследствии глобальной изгибной неустойчивости, дают большее отношение $c_z/c_r$, чем минимально необходимо для устойчивости. Причина связана с существенно нелинейным механизмом разогрева. В результате система проскакивает границу устойчивости по параметру $c_z/c_r$ (см. рис. 3.38).

В моделях с маломассивным гало ($\mu \lee 1$), если диск достаточно горячий, чтобы обеспечить гравитационную устойчивость относительно бар-моды, основным фактором, разогревающим первоначально тонкий диск, является осесимметричная изгибная мода, а моды $m=1,~2$, как правило, не формируются.

Figure: В данной модели ($\mu =4$) начальные условия обеспечивают устойчивость центральной области и изгибная мода $m=0$ развивается в зоне $r\gee L$: а) - зависимость вертикального смещения диска от времени на начальном этапе для различных расстояний от центра; б) - форма диска (центр тяжести по $z$-координате). Толстая линия соответствует $\zeta =0$

=0.999

Figure: Утолщение диска без гало при наличии балджа ($M_b=0,25\,M_d$, $b=~0,2\,L$) в результате развития моды $m=0$. В области балджа вертикальная шкала диска $z_0$ увеличивается слабо. Числа на рисунке -- см. рис. 3.29

=0.5

Отметим, что формирование моды $m=0$ может начинаться не в центре, а на периферии ($r\gee L$), даже не проникая в центральную зону диска. Это возможно в двух случаях: 1) в начальный момент времени в центре отношение $c_z/c_r \ge \alpha_z^{crit}$ обеспечивает устойчивость, а во внешней области диск тонкий и неустойчивый (рис. 3.32); 2) при наличии достаточно массивного или концентрированного балджа. В таких моделях изгибные моды в центре имеют меньшую амплитуду, однако периферия может сильно утолщаться (рис. 3.33). В целом балдж играет стабилизирующую роль, как и гало. Поэтому при прочих равных условиях диски галактик с балджем могут быть тоньше. Однако этот результат требует проверки в моделях с нестационарным балджем, поэтому в п. 3.5.3 при построении моделей конкретных галактик ограничимся выборкой объектов в основном без балджа.

Figure: То же, что на рис. 3.29, но для модели с $\mu =4$ в зоне (кривые 1 -- центр, 19 -- на $r=\frac{8}{3}L$). Вертикальное смещение $\zeta$ для $r<\frac{4}{3}L$ и зоны $\frac{4}{3}L<r<\frac{8}{3}L$ показано на отдельных графиках (соответственно а и б)

=0.999

Figure: То же, что на рис. 3.34$\!$д, но для всего диска (1 -- центр, 30 -- на $r=4L$) и на больших временах. После $t\gee 54$ имеем квазистационарное состояние

=0.5

Учитывая ``катастрофические'' последствия развития осесимметричной изгибной моды (утолщение диска может достигать уровня ), по-видимому, большинство галактик не проходили этой стадии, поскольку она порождает очень толстые диски. Например, в модели с $\mu =1$ (см. рис. 3.29) имеем в среднем $\langle{z_0}\rangle/L\simeq 0,\!4$. В отсутствии гало даже наличие балджа допускает утолщение периферии диска до $z_0\lee 0,\!4\,L$ в результате развития изгибной неустойчивости $m=0$ (см. рис. 3.33). В случае более массивного гало ($\mu =4$) диск, прошедший разогрев изгибной осесимметричной модой, имеет меньшую относительную толщину $\langle{z_0}\rangle/L\simeq 0,\!16$. Однако наблюдения указывают на то, что у ряда галактик величина $\langle{z_0}\rangle/L\le 0,\!15$. Поэтому в этих системах следует либо подозревать очень массивное гало ($\mu > 4$), либо, что осесимметричная изгибная мода не разогревала диск. Отметим, что данный механизм может приводить к образованию центрального утолщения (типа балджа) (см. рис. 3.31) и линзовидных галактик.

Изгибные моды . При более массивном гало ($\mu \gee 2$) в вертикальном разогреве диска на начальной стадии эволюции могут принимать участие неосесимметричные изгибные моды $m=1$ и $m=2$. При этом сохраняется осесимметричное распределение вещества. На рис. 3.34 показана эволюция первоначально тонкого диска с $\mu =4$. В этом случае, в отличие от модели с $\mu =1$ (см. рис. 3.29), на начальной стадии в центральной области диска ($r \lee 2L$) первой формируется изгибная мода $m=2$ (типа ``седло''). Отметим, что и в рамках линейного анализа мода $m=2$ может быть неустойчивой в случае массивного гало [173]. Характерные времена нарастания возмущений и вертикального разогрева могут сильно различаться в центральной зоне диска и на периферии, однако и в этом случае устанавливается конечное квазистационарное состояние (рис. 3.35).

Figure: Структура вертикального смещения $\zeta (x,y)$ в плоскости диска в разные моменты времени: а)  -- в центральной области мода $m=2$; б)  -- начинается перестройка мод $m=2 \rightarrow m=1$; в) $t=3,\!6$; г) $t=4,\!2$ -- развитая однорукавная мода; д) $t=10,\!1$ -- перестройка мод $m=1 \rightarrow m=0$; е) $t=1,\!4$ -- развитая осесимметричная мода; ж) $t=51$ -- в самом центре $r\lee L=0,\!25$ смещения практически затухли, далее наблюдается осесимметричное возмущение, и на периферии мода $m=2$ малой амплитуды

=0.7

На рис. 3.36 изображены распределения величины $\zeta$ в плоскости диска в разные моменты времени для модели, показанной на рис. 3.34. Вертикальный разогрев и, соответственно, утолщение диска, связанное с модой $m=2$, слабое. Но уже после $t\gee 3$ (период обращения внешнего края диска $T_0=2,7$) начинается нелинейная стадия однорукавной моды $m=1$ (асимметричная) и в результате вертикальный разогрев заметно усиливается. Наконец, третий этап разогрева начинается с , и связан он с раскачкой осесимметричной моды $m=0$. На этой стадии увеличение дисперсии скоростей $c_z$ особенно велико, а диск утолщается в 2-3 раза. Таким образом, рассмотренная модель демонстрирует процесс перестройки изгибных мод, последовательный переход от волны $m=2$ к осесимметричной моде.

Как и в случае маломассивного гало, с ростом начального отношения $\alpha _z=c_z/c_r$ (соответственно, увеличения вертикальной шкалы $z_0$) условия для глобальной изгибной неустойчивости ухудшаются и, начиная с некоторых распределений $\alpha_z^{crit}(r)$, коробление не образуется на протяжении, по крайней мере, 20 периодов диска.

Отметим, что в процессе развития изгибной неустойчивости для мод диск не является квазиравновесным в вертикальном направлении в смысле выполнения баланса (3.12). Распределение $c_z(r,\varphi)$ остается осесимметричным, а $z_0$ обнаруживает неосесимметричность. Таким образом, условие $c_z^2/z_0=const$ не выполняется. Для осесимметричной моды соотношение $c_z^2\propto z_0$ выполняется заметно лучше, за исключением самой центральной области, когда диск сильно утолщается.

Figure: а) - зависимость от времени отношения дисперсий $c_z/c_r$ в модели с баром на разных радиусах; б) - структура изгибной моды в процессе формирования бара ($t=15$). Тонкая сплошная линия соответствует вертикальному смещению $\zeta =0$, штриховые линии -- изолинии плотности бара. Коробление бара является причиной быстрого вертикального разогрева в центральной зоне (линии 1, 5 на рис. а) в интервале $t=10\div 20$

=0.999

Разогрев в процессе изгибов бара. Обсудим модели с не очень массивным гало ($\mu\lee 1,5$). Если в начальный момент времени диск гравитационно неустойчив, то возможно рождение бара. При формировании бара в первоначально тонком холодном диске в результате неустойчивости глобальной бар-моды на начальной стадии возможно формирование вертикальных изгибов бара [725]. Рисунок 3.37 демонстрирует изгиб бара, динамика которого приводит к росту дисперсии вертикальных скоростей со временем. Амплитуда коробления бара достаточно быстро уменьшается со временем по мере его утолщения. Подчеркнем, что сформировавшийся бар препятствует в дальнейшем развитию глобальных изгибных мод и, прежде всего, осесимметричной $m=0$.

Мелкомасштабные изгибные возмущения. В случае подавления крупномасштабных изгибных возмущений важным механизмом коллективного разогрева является неустойчивость мелкомасштабных изгибных волн. Амплитуда таких колебаний мала $\vert\zeta\vert \ll z_0$, и они не носят скоррелированного характера. Рост дисперсии скоростей $c_z$ и толщины диска происходит медленно: $\delta =\Oo \left({T_0\, d z_0\o z_0 dt}\right)^{-1} \sim 100$. Причем скорость роста слабо зависит от радиальной координаты, что лишний раз говорит о локальном механизме разогрева. Это отличается от рассмотренной выше глобальной изгибной неустойчивости, для которой относительное время разогрева $\delta$ сильно зависит от $r$, и для моделей на рис. 3.29, 3.34 $\delta\sim 1\div 10$.

Если начальное состояние допускает развитие глобальной изгибной неустойчивости, то конечный диск после установления квазистационарного состояния оказывается устойчивым относительно мелкомасштабных изгибных возмущений. На это указывает отсутствие роста $c_z$ и $z_0$ со временем в моделях, показанных на рис. 3.29, 3.35 (начиная с некоторого момента времени).

Отношение $c_z/c_r$. При прочих равных условиях ключевым параметром, определяющим устойчивость диска, является отношение $c_z/c_r$. В случае если масса сфероидальной подсистемы не слишком велика по сравнению с массой диска, то для стабилизации изгибных возмущений требуются $c_z/c_r$, заметно превышающие значения 0,3-0,37, полученные из линейного анализа для простых моделей [172, 250, 621].

Figure: Радиальные распределения $\alpha _z=c_z/c_r$: а -- $\mu =1$ (см. рис. 3.29); б -- $\mu =4$ (см. рис. 3.34); 1 -- начальная зависимость, 2 -- конечное распределение, 3 -- критический уровень $\alpha _z$; в) --  зависимости от времени $c_z/c_r$ вблизи границы устойчивости (см. линию 3 на рис. б) на разных расстояниях от центра диска

=0.999

Рассмотрим в качестве примера модели без бара с маломассивным гало без балджа с $\mu =1$ (см. рис. 3.29). На рис. 3.38$\!$a изображены начальное (линия 1) и конечное (линия 2) распределения $\alpha_z(r)$. Вертикальный разогрев за счет осесимметричной изгибной моды в данном случае настолько сильный, что в среднем по всему диску $\langle{c_z/c_r}\rangle=0,82$. Немонотонный характер конечного распределения $\alpha_z(r)$ на рис. 3.38$\!$а вызван начальным состоянием (прежде всего $c_z/c_r$), и при других условиях зависимость может быть монотонной. Если в начальный момент времени задать параметр $\alpha_z(r)$ в соответствии с линией 3, то в этом случае изгибные моды оказываются устойчивыми.

С ростом относительной массы гало $\mu$ критические значения отношения $c_z/c_r$ уменьшаются. На рис. 3.38$\!$b показаны начальное (линия 1) и конечное (линия 2) распределения $\alpha_z(r)$ в случае $\mu =4$. Если в момент времени задать параметр $\alpha_z(r)$ в соответствии с линией 3, то в этом случае диск оказывается устойчивым.

Отличительной особенностью построенных нами моделей является неоднородность вдоль $r$-координаты параметра $c_z/c_r$, обеспечивающего устойчивость изгибных возмущений. В случае диска с маломассивным гало ($\mu \lee 1$) при $c_r(r)$, которая обеспечивает подавление бар-моды, для стабилизации изгибной неустойчивости величина $c_z/c_r$ монотонно уменьшается с радиусом: в центральной зоне типичными значениями являются , а на периферии диска (см. рис. 3.38).

Обсудим, как соотносятся $\alpha_z^{crit}$, определяющие границу устойчивости, для мелкомасштабных (МИМ) и глобальных изгибных мод (ГИМ). Если первоначальный диск является очень тонким, то глобальная изгибная неустойчивость является значительно более эффективным механизмом вертикального разогрева. Однако диск оказывается устойчивым относительно ГИМ при меньших значениях параметра $\alpha_z(r)$, чем мелкомасштабные возмущения. Диск может быть устойчивым относительно ГИМ, но неустойчивым для МИМ. Последняя выступает в качестве дополнительного фактора вертикального разогрева. Причем, поскольку этот механизм дает очень медленный разогрев, то конечное состояние не является перегретым, как в результате развития глобальной осесимметричной моды.

Figure: Разными значками показаны положения конечных состояний моделей на плоскости относительной вертикальной шкалы и относительной массы сфероидальной подсистемы

=0.5

Эффект уменьшения относительной вертикальной шкалы диска $z_0/L$ с увеличением относительной массы сфероидальной подсистемы $M_s/M_d$ продемонстрирован на рис. 3.39. Модели различаются параметрами сфероидальной подсистемы, а также начальным распределением $c_r(r)$. У реальных галактик имеются дополнительные факторы вертикального нагрева и утолщения диска. В частности, к ним относятся: волны плотности, гигантские молекулярные облака, приливное взаимодействие. Поэтому определение толщины диска из условия маржинальной устойчивости относительно изгибных возмущений дает оценку снизу на массу гало.

Для построения устойчивого диска относительно изгибных возмущений, чтобы избежать влияния начальных условий, используется серия моделей при фиксированных значениях параметров сфероидальной подсистемы, поверхностной плотности диска $\sigma(r)$, дисперсии скоростей в плоскости диска $c_r$, $c_\varphi$ с различными начальными отношениями $\alpha _z=c_z/c_r$ и выбирается модель, обеспечивающая стационарную вертикальную структуру на субкритическом уровне (распределение $\alpha_z(r)$ минимально необходимое для изгибной устойчивости). Задаваемая зависимость $c_r(r)$ обеспечивает гравитационную устойчивость относительно возмущений в плоскости диска (см. § 3.3).

3.5.3 Результаты моделирования галактик, наблюдаемых с ребра

При построении модели галактики, видимой с ребра, в качестве свободных параметров варьируется масса гало $M_h$ внутри радиуса $R_{\max}$ (который соответствует $r=4L$ или радиусу обрыва диска из наблюдений), радиальная шкала гало $a$ и центральная поверхностная плотность диска $\sigma_0$ [847]. Параметр $\mu=M_s/M_d$ (отношение массы сфероидальной подсистемы $M_s$ к массе диска $M_d$) определяется из условия согласия наблюдаемых и модельных вертикальной шкалы и скорости вращения диска.

В моделях с маломассивным гало ($\mu\lee 0,\!5$) толщина дисков, как правило, получается больше наблюдаемой, в моделях же с очень массивной сфероидальной подсистемой ($\mu > 3$) модельный диск оказывается более тонким, чем наблюдается у рассматриваемых галактик. Оптимальной моделью галактики следует считать ту, в которой вертикальная шкала диска оказывается близкой к наблюдаемой. Такой подход позволяет получать верхние оценки на массу диска (т. к. диски в процессе эволюции могут нагреваться также и за счет действия факторов, не учитываемых в моделях) и, соответственно, нижние пределы на массу темного гало галактик ^3.12.

Table: Параметры галактик, наблюдаемые с ребра

Name	$D$ (мпк)	$L$ (кпк)	$\langle z_0\rangle$ (кпк)	$\langle h_{z}\rangle$ (кпк)	$R_{\max}$ (кпк)	$\mu$
UGC 6080	32,3	2,9	0,69	0,48	7,32	1,0
NGC 4738	63,6	4,7	1,30	0,70	19,20	0,7
UGC 9556	30,6	1,5+3,6	0,51	--	9,00	1,1
UGC 9422	45,6	3,5	0,80	0,51	14,60	0,8
NGC 5170	20,0	6,8	0,82	--	26,20	1,9 (2,0)
UGC 8286	4,8	2,0	0,26	0,13	8,00	1,6
UGC 7321	10,0	2,1	0,17$^a$	0,14$^b$	8,15	3,0
NGC 891	9,5	4,9	0,98	0,49	21,00	1,0 (1,5)

Примечание. $D$ -- расстояние до галактики; $L$ -- экспоненциальная шкала диска; $z_0$ -- усредненная по радиусу вертикальная шкала для закона (3.13);  -- усредненная по радиусу вертикальная шкала для экспоненциального закона; $R_{\max}$ -- радиус обрыва диска; $\mu=M_s/M_d$ -- относительная масса сфероидальной подсистемы $^a$ -- приведена величина $h_{ch}$ для периферии диска; $^b$ -- в центре диска

Параметры дисков приведены в табл. 3.2. Значения вертикальных шкал указаны для двух законов изменения яркости и усреднены по радиусу. При выборе расстояний до галактик UGC 6080, NGC 4738, UGC 9556, UGC 9422 постоянная Хаббла принималась $H_0 = 75$ км/с/кпк. Для $NGC~5170$ и $NGC~891$, помимо вертикальной шкалы, известна и радиальная зависимость дисперсии скоростей звезд, что позволяет при построении динамических моделей проводить согласование по двум параметрам.

В качестве примера подробно рассмотрим модель UGC 9422 [847]. Расстояние до этой галактики составляет $D=45,6$ Мпк. Для радиальной шкалы диска получено $L=16''=3,5$ кпк, для вертикальных шкал: $h_z=2,3''=0,5$ кпк, $z_0=3,6''=0,8$ кпк. Резкий обрыв диска наблюдается на радиусе $R_{\max}=14,6$ кпк, балдж практически не обнаруживается. Кривая вращения (полученная по линии $H_\alpha$) взята из работы [72]. На рис. 3.40$\!$а показаны скорости вращения для этой галактики $V^{obs}$, круговые скорости $V_c$ и приведены скорости вдоль луча зрения $V^{s}$ без учета внутреннего поглощения (см. § 2.6).

Figure: Для галактики UGC 9422: а) - радиальные зависимости $V_c$ (линии 1, 2 -- соответственно для $\mu =0,4$ и $\mu =0,8$), $V^{obs}$ (+ и $\bullet$), $V^{s}$ (линии 3, 4 -- соответственно для $\mu =0,8$ и $\mu =0,4$); б) - модельная вертикальная шкала $z_0$, вертикальная шкала по данным наблюдений $z_0^{obs}$ (+ и $\bullet$)

=0.999

Для этой галактики построена серия моделей, имеющих близкую круговую скорость, но различающихся массой дисковой $M_d$ и сфероидальной компонент $M_h\!$. Как следствие, эти модели имеют разные вертикальные шкалы дисков $z_0$. На рис. 3.40$\!$б показаны радиальные распределения $z_0$ по данным наблюдений и результатам динамического моделирования. В случае маломассивного гало $\mu=0,41$ диск получается заведомо толще наблюдаемого. Этот результат является доводом против модели максимального диска, в которой центральная поверхностная плотность $\sigma_0=1330\,M_\odot/$пк$^2$, а вклад диска в круговую скорость максимален и составляет $V_{c}^{disk}/V_{c}\vert _{r=2,2L}=0,93$.

С ростом массы гало величина $z_0$ уменьшается, и уже при $\mu =0,8$ получаем удовлетворительное согласие с данными наблюдений. В такой модели имеем $M_d=7,5\cdot 10^{10}\,M_\odot$, $M_h=6\cdot 10^{10}\,M_\odot$, $\sigma_0=1060\,M_\odot/$пк$^2$ и $V_{c}^{disk}/V_{c}\vert _{r=2,2L}=0,87$. При менее массивном диске ($\mu =1,6$) выполняется условие $z_0<z_0^{obs}$ (см. рис. 3.40). Полученный результат позволяет считать, что масса дискового компонента не превышает значение $7,5\cdot 10^{10}\,M_\odot$.

Figure: То же, что на рис. 3.40, но для UGC 7321. (а) - данные наблюдений: 1, 2 - закон ${\rm sech}(z/h_{ch})$, 3, 4 - $\exp(z/h_z)$. б) - Символы $+$ и $\bullet$ относятся к разным сторонам диска [612]

=0.999

Галактика UGC 7321 по терминологии Гоада и Робертса [445], относится к числу супертонких, для которых отношение осей $\le 30:1$. По данным [612] балдж отсутствует, $D=10$ кпк, $L=2,1$ кпк, $R_{25}=8,15$ кпк (радиус по 25-й изофоте). Последнюю величину примем в качестве $R_{\max}$ при построении динамической модели. К числу примечательных особенностей галактики относится отсутствие тонкой экваториальной пылевой полосы. В работе [613] приведено радиальное распределение вертикальной шкалы. В центральной области диска используется экспоненциальный закон для вертикального профиля, а на периферии -- функция $\textrm{sech}(z/h_{ch})$ (рис. 3.41$\!$а). Для этой галактики рассчитаны модельные величины $h_{z}$, $h_{ch}$.

Воспользуемся кривой вращения из работы [612]. Для галактик, наблюдаемых с ребра, эффекты проекции и поглощения излучения пылью в наименьшей степени играют роль на периферии диска (см. § 2.6). Поэтому выберем значение систематической скорости $V_{sys}=394$ км/с, что обеспечивает во внешней области для обеих сторон от центра галактики близкие значения скорости $V\simeq 100$ км/с (рис. 3.41б). Если использовать величину $V_{sys}=408$ км/с [612], то в области $r>8$ кпк имеется систематическое различие в $\Delta V\simeq 30$ км/с между скоростью вращения справа и слева от центра диска.

Тонкий диск предполагает наличие достаточно массивного гало. На рис. 3.41$\!$б зависимости 5 и 6 получены в моделях соответственно с относительной массой гало $\mu=2,3$ и $\mu =1,5$ внутри $r<R_{\max}=8,15$ кпк. Как видим, согласие с наблюдаемым распределением вертикальной шкалы имеем в случае $\mu \gee 2,3$. В модели с $\mu=2,3$ для масс компонентов имеем $M_d=0,62\cdot 10^{10}\,M_\odot$, $M_h=1,4\cdot 10^{10}\,M_\odot$. Вклад диска в круговую скорость на радиусе $r=2,3L$ составляет 71 %. Центральная поверхностная плотность диска равна $\sigma_0=250\,M_\odot/$пк$^2$. Последний результат согласуется с выводом [612], что UGC 7321 является галактикой с низкой поверхностной яркостью. Отметим, что вывод о наличии бара, сделанный в работе [710] на основе фотометрических особенностей галактики, очень трудно согласовать с достаточно массивным гало в построенных моделях.

Изложенные в § 3.4, 3.5 результаты указывают на то, что часто используемая в литературе модель максимального диска неприменима для большинства галактик, поскольку не позволяет объяснить данные наблюдений дисперсий скоростей звезд и вертикальных шкал у них.

3.6 Ограничения на параметры Галактики (Milky Way)

Построим серию моделей Галактики, у которых весь звездный диск находится на границе гравитационной устойчивости. В результате получим ограничения на некоторые динамические и кинематические параметры основных подсистем (диска, балджа, гало) [213, 540].

3.6.1 Закон вращения Галактики в околосолнечной окрестности

Наши представления о структуре и физике Галактики меняются по мере уточнения фотометрических и кинематических данных, получаемых из наблюдений. К числу ее важнейших характеристик относится кривая вращения. Имеется значительное число работ, в которых определяется радиальная зависимость скорости вращения динамически холодной компоненты ([177, 325, 345, 575, 819] и др.). Разные галактические подсистемы имеют разную скорость вращения [284]. Звездный диск вращается в целом медленнее газовой компоненты ($V < V_{gas}$, где $V_{gas}(r)$ -- скорость вращения газа и молодых звезд, а $V(r)$ характеризует старое звездное население). При построении модели Галактики важнейшим параметром является круговая скорость вращения $V_c(r)$, которая определяет пространственное распределение гравитационного потенциала и, следовательно, массы. Наряду со звездным и газовым дисками, существенную роль играет и сфероидальная подсистема, о чем свидетельствуют построенные к настоящему времени модели Галактики [ 334, 365, 682, 741, 770]. Дисковая и сфероидальная подсистемы имеют сложную структуру, что выражается в выделении отдельных компонент, различающихся по своим физическим свойствам. В звездном диске можно выделить тонкую и толстую компоненты [284], а в сфероидальной подсистеме -- гало, балдж и ядро.

Одну и ту же кривую вращения можно построить при сильно различающихся параметрах дисковых и сфероидальных компонент. Если привлекать результаты определений поверхностной плотности вещества в окрестности Солнца $\sigma_\odot$, радиальной $L$ и вертикальной $h$ шкал диска из данных наблюдений, то указанная неоднозначность уменьшается. Дополнительные ограничения накладывает на модель Галактики использование данных о дисперсии скоростей звезд. В основе такой возможности лежит естественное предположение о том, что диск, образуемый старым звездным населением, в котором сосредоточена основная масса, гравитационно устойчив. К дополнительным ограничениям на распределения галактического вещества приводит требование устойчивости относительно изгибных возмущений, поскольку накладывает условия на дисперсию вертикальных скоростей $c_z$ и вертикальную структуру диска [53, 172].

При построении моделей кривой вращения, как правило, предполагается выполненным условие $V_{c}=V_{gas}$, то есть при наличии только круговых движений пренебрегают градиентом давления в радиальном балансе сил. Одна из первых моделей Галактики, построенная Шмидтом [770], была развита и существенно уточнена в моделях [130, 188, 265, 334, 365, 682, 741, 755]. Эти осесимметричные модели в ряде случаев заметно различаются массой своих основных компонент. Предложенная в работе [189] семикомпонентная модель Галактики выявила роль градиентов давления для кривой вращения в отдельных областях. Построение неосесимметричных моделей, в частности, включающих бар, возможно только методом динамического моделирования [429, 430].

Figure: Кривые вращения Галактики, полученные в работах: 1) [345] (сплошная толстая линия) по данным $HI, CO$, $R_\odot =8,5$ кпк; 2) [819] (штриховая линия) $CO$, $H_\alpha$, $R_\odot =8,5$ кпк; 3) [40] (пунктирная линия) по лучевым скоростям и собственным движениям классических цефеид, $R_\odot =7,1$ кпк; 4) [42] (сплошная тонкая линия) для случаев $R_\odot =7,5$ кпк и $R_\odot =8,5$ кпк; 5) [41] (штрих-пунктирная линия) по кинематическим параметрам системы OB-ассоциаций, $R_\odot =7,1$ кпк; 6) [669] (значки показывают: $\circ$ - по линии 21 см, $\boxmy$ -- $HI$, ${\bf +}$ -- $CO$), $R_\odot =8.2$ кпк; 7) [325] (скорость вращения по HI -- $\star$, для областей HII -- $\bullet$) $R_\odot =8,5$ кпк; 8) [246] (значки $\Delta$ показывают скорость вращения, полученную из анализа кинематики планетарных туманностей и AGB-звезд) $R_\odot =7,9$ кпк

=0.999

Кривая вращения для молодого населения Галактики определялась во многих работах (на рис. 3.42 приведены данные наблюдений разных авторов). При построении галактической кривой вращения используют кинематические данные не только газовой компоненты, но и других объектов (OB-звезд, планетарных туманностей, цефеид, HI и HII областей, углеродных звезд). Все эти кривые вращения, в основе которых лежат данные наблюдений молодого населения, будем обозначать $V_{gas}$.

Отметим две характерные особенности на наблюдаемой кривой вращения Галактики (см. рис. 3.42): 1) локальный минимум (прогиб) в окрестности орбиты Солнца ( $r\simeq 6\div 11$ кпк); 2) локальный внутренний максимум внутри центрального килопарсека. Обсудим, к каким последствиям приводит учет этих особенностей при построении модели круговой скорости в предположении $V_c=V_{gas}$. Для определенности выберем кривые вращения из работ Софи [819, 820] (см. толстую сплошную и штриховую линии на рис. 3.42). Сделанные в данной работе выводы не зависят от некоторого различия в кривых вращения у разных авторов, которые используют разные значения $R_\odot$ и разные объекты наблюдений. Так, например, при изменении величины $R_\odot$ в пределах $7,5\div 9,5$ кпк скорость вращения в работе [325] меняется незначительно. При варьировании параметров $R_\odot$ и $V_{gas\,\odot}$ изменяются абсолютные значения пространственных шкал разных компонент и их массы в динамических моделях, но относительные величины меняются слабо.

Обсудим указанные особенности кривой вращения Галактики.

Figure: =0.95I<>а - круговая скорость $V_c$ в модели бесконечно тонкого диска (сплошная линия 6). Крестики -- скорость вращения по работам [820, 819] (см. рис. 3.43). Показаны вклады в круговую скорость: от 1-го диска ( $L_{\sigma 1}=3$ кпк, диск обрывается на 6 кпк, кривая 1); 2-го диска ( $L_{\sigma 2}=6$ кпк, диск обрывается на 14 кпк, кривая 2); гало (кривая 3); балджа (кривая 4); суммы двух дисков (кривая 5); б - профили поверхностной плотности $\sigma$ [$M_\odot /$пк$^2$] дисковых компонент для модели, изображенной на рис. 3.43$\!$а; в - радиальная зависимость круговой скорости $V_c$ и соответствующие вклады дисковых компонент (диск 1 и диск 2), балджа, гало в случае диска конечной толщины с вертикальной шкалой $z_0=0,5$ кпк. Относительная масса гало внутри 12 кпк $\mu =0,51$. Обозначения аналогичны рис. 3.43$\!$а; г - радиальные распределения поверхностной плотности от двух дисков и сумма этих распределений в модели, изображенной на рис. 3.43$\!$в. д - круговая скорость в модели с более массивным гало $\mu =1,9$ (внутри 12 кпк) и бесконечно тонким диском. е - радиальные профили поверхностной плотности для модели, изображенной на рис. 3.43$\!$д

=0.999

Локальный прогиб на круговой скорости вращения в солнечной окрестности может быть обусловлен особенностью распределения плотности в дисковой компоненте [669, 670], либо в гало. В первом случае можно предположить, что радиальное распределение поверхностной плотности описывается, например, суммой двух экспоненциальных законов с разными радиальными шкалами $L_{\sigma 1}$ и $L_{\sigma 2}$, причем диск с короткой шкалой должен резко обрываться в области $r\simeq 6\div 7$ кпк, а второй диск -- на радиусе $r\simeq 12\div 15$ кпк. Круговая скорость для такой модели с достаточно массивным диском (суммарная масса $M_d=7\cdot 10^{10}\,M_\odot$) в случае бесконечно тонкого диска ($z_0 = 0$) показана на рис. 3.43$\!$а. Для амплитуды прогиба $\Delta V = 15$ км/с необходимо, чтобы суммарная поверхностная плотность в узкой зоне $r=(6\div 6,4)$ кпк уменьшалась примерно в 2 раза (рис. 3.43$\!$б). Гравитационный вклад от вещества диска является доминирующим в области $3\,\textrm{кпк}\lee r\lee 15\,\textrm{кпк}$. Данная модель является моделью максимального диска, что как будет показано в п. 3.6.3, не позволяет получить согласие с наблюдаемыми значениями дисперсии скоростей звезд.

Учет конечной толщины диска уменьшает величину $\!\Delta V\!$ до 6 км/с при $\!z_0 = 500$ пк (рис. 3.43$\!$в,$\!$г). С увеличением массы гало (уменьшением массы диска) величина $\!\Delta V$ уменьшается, поскольку относительный вклад дисковой компоненты в круговую скорость вращения в соответствии с (3.18) становится меньше. В случае бесконечно тонкого диска для получения прогиба $\!\Delta V = 9$ км/с в модели с более массивным гало $\mu=M_h(4L)/M_d = 1,\!9$ (рис. 3.43$\!$д) необходим перепад поверхностной плотности $\sigma(r=5,\!8\textrm{кпк})/\sigma(r=7\,\textrm{кпк})\! \gee\! 3$ (!) (рис. 3.43$\!$е). При фиксированном перепаде поверхностной плотности с увеличением вертикальной шкалы до наблюдаемых значений $z_0\simeq~500$ пк величина прогиба уменьшается до значений $\Delta V=3$ км/с.

Если обратиться к другим $S$-галактикам, то заметные отклонения от экспоненциального фотометрического профиля наблюдаются либо на краю галактики [561, 564], либо в центре в виде центральной депрессии звездного диска [12]. Одним из объяснений универсального характера экспоненциального распределения яркости дисковой компоненты могут являться особенности эволюции вязкого газа совместно с процессом звездообразования [394]. Расчеты показывают, что указанные факторы за несколько миллиардов лет формируют экспоненциальный профиль звездного диска, независимо от первоначального распределения газа. Наличие области резкого уменьшения поверхностной плотности на расстоянии $6\div 7$ кпк от центра Галактики не находит прямого подтверждения по данным наблюдений.

Прогиб $V_c(r)$, в принципе, можно получить и за счет особенностей в распределении плотности в гало, однако, это потребует более резкого уменьшения объемной плотности вблизи $r \simeq 6$ кпк, чем у диска (см. рис. 3.43). Если у диска диаметр эпициклического движения в окрестности орбиты Солнца составляет $\Delta r=2 c_r/\varkappa\simeq 2$ кпк, что несколько меньше области прогиба, и, в принципе, построение такого скачка в распределении плотности возможно, то в гало, где типичные дисперсии скоростей имеют порядок 100 км/с, пространственно узкий в радиальном направлении перепад в распределении вещества не может быть долгоживущим.

Имеется дополнительный довод против реальности сильного локального прогиба у круговой скорости вращения $V_c(r)$, следующий из кинематических данных. Для бесстолкновительной системы движение частиц происходит по эпициклическим орбитам, что приводит к условию (3.19) .

Figure: Для кривой вращения $V=r\Omega$ -- левая вертикальная ось ([819], см. кривую  2 на рис. 3.42), приведены радиальные зависимости параметров $2\Omega /\varkappa$ и (правая вертикальная ось). Максимумы у величин $n$ и $2\Omega /\varkappa$ в области $r\simeq 8$ кпк обусловлены локальным прогибом кривой вращения $V$

=0.52

На рис. 3.44 показаны радиальные зависимости параметров и для кривой вращения Софи [819]. В области $r=8\div 10$ кпк имеем значительное изменение параметра $S\simeq 1\div 2,\!1$. Причем, в окрестности Солнца $2\Omega/\varkappa\simeq 1,\!7$, что в соответствии с (3.19) дает $c_r/c_\varphi\simeq 1,\!7$. Обратимся к данным наблюдений. Для старого звездного населения в окрестности Солнца отношение $c_r/c_\varphi \simeq 1,\!55$ [369], что дает $n=1,15$. В результате имеем практически плоскую кривую вращения $V\propto r^{-0,15}\!$. Для молодых звезд, по данным работы [41] $c_r/c_\varphi = 8,\!2/5,\!8=1,\!41$, что также приводит к $V\simeq {\rm const}$. Анализ распределения скоростей ближайших звезд из базы данных Hipparcos дает, что линейная скорость вращения в солнечной окрестности практически не изменяется с радиусом $V \propto r^{-1/9}$ [370].

В работе [177] определены дисперсии скоростей молодых звезд (цефеид и молодых звездных скоплений) $(c_r, c_\varphi, c_z) = (15,\!0; 10,\!3; 8,\!5)$ км/с. Возраст этих объектов составляет в среднем 10 млн лет. Особый интерес представляет близость параметра $c_r/c_\varphi = 1,\!46$ к отношению $2\Omega /\varkappa$, если считать $n=1,\!06$ ( $V\propto r^{-0,06}$). Это означает, что характерное время выстраивания эпициклического движения составляет заведомо меньше одного периода галактического вращения.

Таким образом, имеются аргументы в пользу того, что наблюдаемый прогиб кривой вращения газовой компоненты и молодых звезд, по-видимому, обусловлен не особенностями радиального распределения гравитирующего вещества, а является динамическим феноменом, и может быть связан с некруговыми движениями вследствии прохождения спиральной волны плотности. Конкретным динамическим процессом, приводящим к некруговым движениям, по-видимому, является гигантский антициклон, состоящий из газа и молодых звезд [417].

Отметим, что изучение кинематики OB-звезд и классических цефеид в интервале $r=6\div 12$ кпк не противоречит выводу о постоянстве скорости вращения Галактики в этой области [423]. В то же время кинематика планетарных туманностей, звезд c пылевыми оболочками, углеродных звезд обнаруживает минимум скорости вращения на $r=8,5$ кпк в солнечной окрестности [246] (треугольники на рис. 3.42). Если предположить, что локальный прогиб вызван спиральной структурой, то в этом случае амплитуда таких возмущений должна быть значительной [246].

3.6.2 Кинематика центральной области,
концентрированный балдж и бар

Принято считать, что скорость вращения холодной подсистемы в центральной области $r\lee 1$ кпк имеет ярко выраженный максимум на радиусе $r\simeq 0,3$ кпк [345, 819, 820]. Если предположить равенство $V_c=V_{gas}$, то для объяснения центрального максимума у круговой скорости необходимо учитывать массивный балдж с концентрированным ядром, для параметров которого в модели распределения вещества Кинга следует принять $a_n\simeq 100$ пк, $M_b\simeq 0,\!6\cdot 10^{10}\,M_\odot$ и $r_b^{\max}\simeq 0,\!8$ кпк. Центральная плотность сфероидальной подсистемы ^3.13 в этом случае превышает $400~M_\odot/\textrm{пк}^3$.

Figure: Зависимость от времени интегральных амплитуд фурье-гармоник для азимутальных чисел $m=1,2,\ldots,6$ в модели с массивным концентрированным ядром. Происходит образование бара, который затем разрушается, на что указывает уменьшение амплитуды для гармоники $m=2$. Момент времени $t=30$ соответствует 2,8 млрд лет

=0.41

Figure: Изолинии поверхностной плотности в модели, изображенной на рис. 3.45, в разные моменты времени (см. положения стрелок на рис. 3.45). Показана только центральная область диска

=0.999

Однако концентрированный и массивный балдж не позволяет сформировать долгоживущий бар в динамических моделях [213]. Происходит его вековое разрушение, механизм которого аналогичен действию массивной центральной черной дыры [463]. Уровень неосесимметричности в распределении вещества в диске в каждый момент времени удобно характеризовать амплитудой фурье-гармоник (3.24). На рис. 3.45 показана временная зависимость интегральных амплитуд $\hat{A}$ (3.24). Величина определяет амплитуду двухрукавной моды и, в частности, бара (рис. 3.46). Происходит диссипация бара, причем симметризация идет от самых центральных областей на периферию диска, что обусловлено механизмом разрушения бара. Отметим, что квазипериодический характер зависимости $\hat{A}(m=2,t)$ на рис. 3.45 связан с обменом энергии между бар-модой ($A(p=0,m=2)$) и спиральными волнами. Со временем в процессе эволюции динамической модели происходит уменьшение этого параметра, что указывает на диссипацию волн с $m=2$ (в частности, бара) и установление исходного осесимметричного распределения вещества в диске. Как показали модели с различными параметрами балджа, при уменьшении массы центральной сферической подсистемы (балдж + ядро) и(или) увеличении шкалы ядра балджа $a_n$ время жизни бара увеличивается. Это накладывает ограничения на параметры балджа. Таким образом, концентрированный массивный балдж ($a_n\lee 100$ пк, $\varrho_{b0}\gee 400\,M_\odot/$пк$^3$) оказывается невозможно согласовать с наличием долгоживущей центральной перемычки.

Вывод о возможном разрушении бара при наличии концентрированного ядра у балджа, полученный при построении моделей Галактики [213], справедлив и в общем случае. Таким образом, время жизни бара может зависеть от шкалы ядра и массы балджа.

Figure: =0.83Дисперсии радиальных скоростей звезд $c_r(r)$. По данным наблюдений: $\bullet$ -- [369, 575]; $\circ$ -- дисперсия скоростей гигантов позднего типа внутри 0,3 кпк [310,311]; $\Delta$ -- [732]; $\boxmy$ -- [639]. По результатам моделирования (модели различаются параметрами гало и балджа, $\mu = M_h/M_d$ определяется внутри $4L=12$ кпк): 1 -- $\mu =0,95$; 2 -- $\mu =1,42$; 3 -- $\mu =1,5$; 4 -- $\mu =1,6$. Первые три модели включают концентрированное ядро со шкалой $a_n\le 100$ пк, в четвертой модели ядро отсутствует и шкала балджа составляет $a_b = 200$ пк. C ростом массы гало $c_r$ уменьшается. В центральной области $r\lee 2$ кпк для уменьшения дисперсии радиальных скоростей до значений $100\div 120$ км/с необходимо рассматривать балдж со шкалой $a_b\gee 200$ пк

=0.58

Отметим еще одно дополнительное соображение против очень концентрированного распределения массы в балдже. Оно связано с наблюдаемыми вдоль луча зрения значениями дисперсии скоростей гигантов позднего типа внутри области $0,3$ кпк $c^{obs}= 128\pm 14$ км/с [310, 311]. Авторы полагают, что эта величина характеризует звезды балджа, следовательно, дисперсия скоростей дисковой компоненты должна быть меньше. Выборка K-гигантов в области 500 пк от центра характеризуется $c_r^{obs} = 104\pm 10$ км/с [732]. Левис и Фриман [575] получили для центральной дисперсии скоростей звезд диска значение $c_r^{obs}=106$ км/с. На рис. 3.47 показаны радиальные распределения дисперсии скоростей $c_r$ для звезд диска из данных наблюдений и по результатам динамического моделирования для разных относительных масс диска. Тонкими линиями изображены модели с массивным концентрированным ($a_n\simeq 100$ пк) балджем, который обеспечивает круговую скорость вращения в центре в соответствии с рис. 3.42. Если в области $r\gee 3$ кпк при определенной массе диска удается согласовать наблюдаемые и модельные значения $c_r$, то в центре диска дисперсия скоростей, полученная в динамических моделях, превышает 130 км/с (кривые 1, 2 на рис. 3.47). Согласование дисперсии скоростей в центре диска оказывается возможным только в моделях с большей шкалой балджа $a_n \gee 200$ пк (толстая линия на рис.  3.47). В этом случае объемная центральная плотность балджа не превышает $100\,M_\odot/$пк$^3$, а масса балджа составляет $\lee 10^{10}\, M_\odot$.

Радиус бара, по данным разных авторов, лежит в пределах $r_{bar}=~ 2\div 4,5$ кпк, отношение полуосей бара в плоскости диска оценивается в , угол между большой осью бара и направлением на Солнце составляет [439, 835, 891]. При сравнении результатов моделирования с наблюдениями примем $\varphi _{bar}=20^\circ$, $r_{bar}= 3,2$ кпк. Поэтому динамическая модель должна допускать существование долгоживущего бара с отношением полуосей не меньше $1,6$. С этой точки зрения модели с массивным и концентрированным балджем с $a_b \simeq 100$ пк не объясняют наблюдаемый бар. Если даже на начальной стадии эволюции холодного диска начинает формироваться бар, то в дальнейшем он разрушается из-за рассеяния на центральном потенциале ядра балджа.

Figure: а - распределение в плоскости диска поверхностной плотности $\sigma (x,y)$. Звездочка отмечает положение Солнца. Угол между большой осью бара и прямой, проходящей через центр диска и окрестность Солнца, составляет $\varphi _{bar}=20^\circ$;  б - cкорость вращения вещества диска $V$ как функция расстояния от центра вдоль разных направлений: $\bigcirc$ -- $V(x)$; $\triangle$ -- $V(y)$. Показана также усредненная по азимутальному углу скорость вращения ($\bullet$)

=0.999

В рамках моделей с $a_n \gee 200$ пк и $M_b\simeq 10^{10}\,M_\odot$ не удается объяснить резкий центральный максимум у круговой скорости $V_c$, однако возможно согласование наблюдаемых и модельных значений дисперсии скоростей в центре и формирование долгоживущего бара. На рис. 3.48$\!$а, б, в показаны изолинии поверхностной плотности и дисперсии скоростей при наличии центральной перемычки. Из-за особенностей движения вещества в области бара, скорость вращения звезд в модели в центре заметно различается вдоль большой и малой осей бара (рис.  3.48$\!$г). Вдоль $x$-координаты скорость вращения звезд $V$ в модели имеет характерный максимум вблизи центра (который отсутствует в направлении Солнце-галактический центр, вдоль $y$-координаты).

Figure: Профили объемной плотности центрально-симметричного балджа в плоскости $z=0$: 1 -- по данным фотометрических наблюдений подгонялась зависимость $\propto \exp(-(r/1,\!9$ кпк $)^2)/(1~+~r/0,\!1$ кпк$)^{1,8})$ [298]; 2 -- в соответствии с законом Кинга (3.5) для $b=0,\!1$ кпк; 3 -- для $b=0,\!2$ кпк. Нормировка $\varrho$ -- произвольная

=0.5

Таким образом, отказ от предположения $V_c=V_{gas}$ в области центрального пика на кривой вращения, во-первых, позволяет согласовать с наблюдениями дисперсию скоростей звезд в центре, а во-вторых, дает возможность объяснить существование долгоживущего бара. При этом локальный максимум скорости может быть обусловлен движением вещества в несимметричном потенциале в области бара, либо наличием внутреннего диска или кольца [409]. Заметим также, что используемая модель Кинга для описания плотности вещества в балдже в случае $b \simeq 0,2$ кпк лучше согласуется с инфракрасным фотометрическим профилем балджа (по данным COBE/DIRBE) в области $100~\textrm{пк}\lee r\lee 0,5$ кпк [298], чем при $b\simeq 0,1$ кпк (рис. 3.49).

3.6.3 Распределение вещества в диске

В соответствии с п. 3.6.1 будем считать, что на периферии Галактики круговая скорость не имеет заметного прогиба. Поэтому будем рассматривать экспоненциальные профили поверхностной плотности $\sigma(r)=~\sigma_0\exp(-r/L)$ с $L=\textrm{const}$. Наблюдения не позволяют надежно определить радиальную шкалу $L$, оценки которой находятся в широких пределах $L=2\div 5$ кпк ([298, 408, 409, 432, 439, 458, 523, 536] и ссылки в этих работах). Более надежными для определения радиальной шкалы диска считаются данные, основанные на наблюдениях в ближнем ИК-диапазоне ($L=2\div 3,5$ кпк). Возьмем в качестве базовой модели диск с $L=3$ кпк. Для балджа будем использовать модель Кинга (3.3) с $a_b=0,2$ кпк и $\varrho_{b0}=72\,M_\odot/\textrm{пк}^3\!$.

Оценки $(h_{exp})_\odot$ для старого диска лежат в пределах от 200 пк до 350 пк [469, 730, 861]. Причем возможен положительный градиент вертикальной шкалы с ростом радиальной координатой [432, 536]. По данным [298], в центральной области $h_{exp}<210$ пк. В работе [284] после вычитания вклада от звезд толстого диска вертикальная шкала старого диска составляет $h_{exp}\simeq 330$ пк. Вертикальное распределение M-карликов лучше аппроксимируется комбинированным законом $\varrho\propto 0,8\cdot\textrm{ch}^{-2}(z/323\,\textrm{пк}) + 0,2\cdot\exp(-\vert z\vert/656\,\textrm{пк})$ [357], что приблизительно соответствует значениям $z_0=400$ пк в области $\vert z\vert<1$ кпк. Однако поверхностная плотность M-карликов не превосходит значение $\sigma=14\,M_\odot/$пк$^2$ и составляет меньшую часть от суммарной плотности диска [357]. Однако данные COBE/DIRBE [375] и 2MASS [594] приводят к вертикальному масштабу диска Галактики около 0,28 кпс.

Рассмотрим ограничения на поверхностную плотность в солнечной окрестности $\sigma_\odot$. По-видимому, к числу наиболее точно установленных параметров в солнечной окрестности диска относятся дисперсии скоростей звезд. Следуя [369], для наиболее старого звездного населения примем $(c_r,c_\varphi,c_z)=(38,\,24,\,20)$ км/с.

Figure: =0.9Зависимость параметров модели от поверхностной плотности диска на радиусе $R_\odot =$8 кпк: (а) - дисперсия радиальных скоростей при различных радиальных шкалах диска $L=$2, 3, 4 кпк. Горизонтальная линия -- наблюдаемое значение $c_r=38$ км/с. Вертикальная линия -- поверхностная плотность вещества $\sigma_\odot=71\pm 6\,M_\odot/\textrm{пк}^2$, которая заключена в пределах $\vert z\vert<1,1$ кпк, по данным [565]; (б) -  шкала гало $a$ в соответствии с (3.3) для серии моделей с радиальной шкалой диска $L=3$ кпк; (в) - масса гало $M_h$ и отношение массы гало к массе диска внутри различных радиусов ($r=6$ кпк$=2L$, $8$ кпк, $12$ кпк$=4L$)

=0.6

На рис. 3.50$\!$а по результатам динамического моделирования представлена зависимость дисперсии радиальных скоростей звезд, обеспечивающая при заданной массе гало гравитационную устойчивость диска, от поверхностной плотности в окрестности Солнца $\sigma_\odot$. Результаты моделирования в случае $L=3$ кпк показаны значком `` $\star$ ''. При больших значениях поверхностной плотности $\sigma_\odot\gee 70\,M_\odot/\textrm{пк}^2$ величина $c_r$ заведомо превышает наблюдаемое значение $c_r=38$ км/с. В случае малой поверхностной плотности $\sigma_\odot\lee 40\,M_\odot/\textrm{пк}^2$ имеется значительный запас устойчивости. Наилучшее согласие между моделью и наблюдениями достигается при $\sigma_\odot\simeq 58\,M_\odot/\textrm{пк}^2$. В этом случае шкала гало примерно в два раза превышает радиальную шкалу диска $a_h/L = 6,3\,\textrm{кпк}/3\,\textrm{кпк}$ (рис. 3.50$\!$б), и внутри сферы радиуса $R_\odot = 8$ кпк для массы гало имеем $M_h=3\,\cdot 10^{10}\,M_\odot$, что составляет 87 % от массы диска (рис. 3.50$\!$в). Общая масса диска в такой модели достигает $4,4\,\cdot 10^{10}\,M_\odot$ (в пределах 12 кпк), а центральная поверхностная плотность составляет $\sigma_0=840\,M_\odot/$пк$^2$. Вклад диска в круговую скорость на радиусе $r=2,2L$, где достигается максимум $V_c^{disk}$ для экспоненциального профиля поверхностной плотности, составляет $(V_c^{disk}/V_c)_{\big\vert\, r=2,2L}=0,73$. Вклад балджа в круговую скорость в этой модели составляет на радиусе $r=2,2L$ $(V_c^{bulge}/V_c)_{\big\vert\, r=2,2L}=0,43$. Отметим, что близкий результат $(V_c^{disk}/V_c)_{\big\vert\, r=2,2L}=0,76$ получен в модели [429] в случае $L=3$ кпк.

В пределах $r=4L=12$ кпк для относительной массы гало имеем $\mu=M_h/M_d=1,6$, что согласуется с результатом анализа вертикальной структуры диска ($\mu = 1,8$) [267]. Нашу Галактику можно считать типичной системой, у которой темное вещество гало не только определяет кинематику внешних областей $r>12$ кпк, но и играет заметную динамическую роль в области звездного диска ($r<4L=12$ кпк). Полученная оценка на поверхностную плотность диска $\sigma_\odot = 58\,M_\odot/\textrm{пк}^2$ свидетельствует о том, что вклад диска в вертикальный баланс сил является определяющим. В то же время данные наблюдений дают достаточно большой разброс поверхностной плотности в солнечной окрестности $\sigma_\odot=39\div 71\,M_\odot/\textrm{пк}^2$, хотя наиболее надежными представляются значения $50\div 60\,M_\odot/\textrm{пк}^2$ [755].

Измерения радиальной шкалы диска лежат в пределах $L = 3\pm 1$ кпк [755], причем как для тонкого, так и для толстого звездных дисков. Рассмотрим модели с большей шкалой диска $L=4$ кпк (см. рис. 3.50$\!$а). В этом случае, чтобы диск находился на границе устойчивости, плотность $\sigma_\odot$ должна составлять $\simeq 80\,M_\odot/$пк$^2$, что противоречит данным наблюдений [439, 448, 565]. Согласовать поверхностные плотности возможно только в предположении, что диск имеет значительный запас гравитационной устойчивости  км/с км/с. Если принять во внимание весь диск, а не только солнечную окрестность, то оказывается, что согласие между радиальными распределениями $c_r$ и $c_r^{obs}$ в моделях с $L=4$ кпк существенно хуже, чем в случае $L=3$ кпк  ^3.14.

В случае короткой шкалы $L=2$ кпк при фиксированном значении $R_\odot = 8$ кпк даже в модели максимального диска, для которой $(V_c^{disk}/V_c)_{\big\vert\, r=2,2L}=0,89$, на границе устойчивости имеем  км/с, и поверхностная плотность мала $\sigma_\odot=33\,M_\odot/$пк$^2$ (см. рис. 3.50$\!$а). Масса сфероидальной подсистемы в области $r<4L=8$ кпк составляет всего 63 % от массы диска. Таким образом, имеется запас устойчивости, поскольку увеличить величину $\sigma_\odot$ до значений $50\,M_\odot/$пк$^2$ (соответственно, дисперсию радиальных скоростей до наблюдаемой величины $c_r^{obs}=38\,\textrm{км/с}$) не удается в рамках заданной кривой вращения. Итак, модели с $L=3$ кпк лучше удовлетворяют совокупности данных наблюдений, чем диски со шкалой $L=2$ кпк или $L=4$ кпк.

В динамической модели, которая согласуется с наблюдаемыми кривой вращения холодной компоненты, скоростью вращения звезд и дисперсиями скоростей старого диска, получаем для общей объемной плотности на радиусе $R_\odot = 8$ кпк, $\varrho_\odot=0,068\,M_\odot/\textrm{пк}^3$ (на долю дисковой компоненты приходится $\varrho_{\odot}^{disk}=0,058\,M_\odot/\textrm{пк}^3$). Разность $\varrho_{\odot}^{s}=~\varrho_\odot-\varrho_{\odot}^{disk}=0,\!01\,M_\odot/\textrm{пк}^3$ относится к сфероидальной компоненте -- гало и толстому диску. Полученная объемная плотность не противоречит последним данным наблюдений $\varrho_{\odot, obs}=0,076\pm 0,015\,M_\odot/\textrm{пк}^3$ [360]. Если поверхностная плотность диска в солнечной окрестности составляет всего $\sigma_\odot^{obs}=40\,M_\odot/\textrm{пк}^2$ [357], тогда это указывает на запас гравитационной устойчивости звездного диска и на большую массу гало по сравнению с диском внутри $r=8$ кпк.

3.6.4 Кинематика старого звездного диска.
Эллипсоид скоростей звезд ( $c_r, c_\varphi , c_z$)

Figure: Скорости вращения звезд диска $V^{obs}$ по данным [575] ($\boxmy$), [284] ($\bigoplus$). Толстая линия описывает модель с $\mu =1,6$, а пунктирная -- $\mu =0,9$. Круговая скорость изображена значком $\Delta$

=0.45

Динамические модели наглядно показывают, что с уменьшением массы гало увеличивается разница между круговой скоростью вращения $V_c$ и скоростью вращения вещества в диске (звезд) $V\!$. Этот эффект следует из (3.17) и обусловлен увеличением вклада теплового движения звезд в радиальном балансе сил. Таким образом, разница между круговой скоростью и скоростью вращения старого населения предоставляет возможность независимой оценки массы диска. По данным наблюдений [575], скорость вращения старого звездного населения в области $r>5$ кпк превышает 200 км/с. В работе [284] в окрестности Солнца для скорости вращения звезд в плоскости $z=0$ получено 200 км/с. Таким образом, разница в скорости вращения между наиболее молодыми и старыми звездами не превышает $20$ км/с. Последнее обстоятельство является дополнительным фактором в пользу не очень массивного звездного диска (рис. 3.51). Если внутри орбиты Солнца на долю диска приходилось бы больше 70 % массы, то разность между круговой скоростью $V_c$ и скоростью вращения старого звездного диска $V$ была бы не меньше 35 км/с (модель с $\mu =0,9$ на рис. 3.51).

Figure: Радиальные зависимости параметров дисковой компоненты для оптимальной динамической модели Галактики в сравнении с данными наблюдений. Здесь (а) - кинематические параметры: кривая вращения (сплошная линия), круговая скорость $V_c$, скорость вращения диска в модели $V\!$, наблюдаемая дисперсия скоростей $c_r^{obs}$, модельные дисперсии скоростей $c_r$, $c_\varphi$, $c_z$; (б) - радиальные зависимости отношения $c_z/c_r$ (ромб) и параметра $Q_c$ ($+$) (левая ось), поверхностной плотности $\sigma$ (сплошная и пунктирная линии, правая ось)

=0.999

=0.95

На рис. 3.52$\!$а показаны радиальные зависимости параметров динамической модели, которая наилучшим образом согласуется с наблюдаемым распределением дисперсий скоростей звезд в окрестности Солнца $(c_r,c_\varphi,c_z)=(38,24,20)$ км/с [369] и, следовательно, $c_r/c_\varphi=1,58$; $c_z/c_r=0,53$.

На рис. 3.52б показаны для этой модели профиль поверхностной плотности $\sigma(r)$, $Q_c\equiv c_r\varkappa/2\Omega c_\varphi$, $c_z/c_r$, штриховой линией изображен экспоненциальный профиль со шкалой $L=3$ кпк. Для всего диска выполняется $Q_c\simeq 1$. Отношение дисперсий $\alpha _z=c_z/c_r$ монотонно уменьшается с удалением от центра, где $\alpha_z(r=0)\simeq 0,7$. На периферии Галактики за радиусом орбиты Солнца имеем всего $\alpha_z(r>10$ кпк$)\simeq 0,4$.

3.7 Асимметричные галактики (lopsided-галактики)

У ряда галактик поздних типов с отчетливо выраженным баром наблюдается смещение бара относительно центра диска. Классическим примером является Большое Магелланово Облако, у которого центры распределений яркости диска, планетарных туманностей, сверхгигантов, $HI$ и бара не совпадают [872]. Кинематический центр диска смещен относительно бара в БМО примерно на $0,7\div 1,2$ кпк [544, 818]. Такая картина является достаточно распространенной у галактик позднего типа. Примерами являются NGC 55 [499, 738], NGC 1313, 4490, 4625, 4027 [347, 405, 601], NGC 1744 [381, 707]. Причем, если наблюдается двухрукавная спиральная структура, то она, как правило, несимметрична -- одна ветвь заметно более развита по сравнению с другой. Например, Писано и др. [707] отмечают, что у NGC 925 имеется одна мощная спиральная ветвь, а вторая является фрагментарным образованием.

Смещенный бар и спиральная однорукавная структура являются типичными отличительными чертами SBcd -- SBm-галактик (=Магелланова типа) [872]. Эти свойства наиболее ярко демонстрируют, например, БМО и NGC 4618, у галактики NGC 925 (SAB(s)d) они проявляются в менее яркой форме, и принято считать, что степень асимметрии непрерывно меняется при переходе к галактикам более позднего типа [708]. Фейтзингер [393] отмечает, что величина смещения центра бара во многих случаях составляет половину от радиальной шкалы диска $L$, хотя в некоторых случаях смещение меньше этого значения. Смещение центра бара относительно центра внешних изофот у NGC 4618 достигает 660 пк при $L=900$ пк [678]. У NGC 925 расстояние между центром бара и динамическим центром составляет $\sim 950$ пк при радиальной шкале внешнего диска $L=4,2$ кпк [708]. Причем,по данным [707], у этой галактики не совпадают центр бара $\vec{r}_{bar}$, центр галактики согласно RC3, центр внешних инфракрасных изофот и динамический центр. Отметим, что авторы связывают эту асимметрию с облаком газа $10^7\,M_\odot$, которое взаимодействует с основной галактикой, но отмечают, что силы этого взаимодействия недостаточно.

Следует подчеркнуть, что смещение бара является одной из форм нарушения симметрии галактических дисков. Последние исследования показывают большое распространение асимметричных галактик (lopsided galaxies) прежде всего среди поздних типов [752] и особенно среди карликовых систем [472]. Однако отдельные проявления асимметрии обнаруживаются и в дисках галактик раннего типа [751].

Моделирование образования баров методом N-тел показало важные отличия свойств центральных перемычек в галактиках позднего и раннего типов [349, 777]. В работах [239, 254, 760, 763, 777] изучалась динамика дисковых компонент в гравитационном поле бара с заданным смещением. При построении моделей асимметричных галактик в работах Левайн и Спарк [578], Нордемир и др. [672] смещение центра гало относительно центра диска задавалось изначально, без рассмотрения механизмов, приводящих к нарушению осевой симметрии в распределении вещества.

В связи с проблемой формирования смещенных баров обсуждались механизмы, связанные с начальной асимметрией протогалактики и особенностями последующей аккреции на диск. Одной из причин смещения бара может являться сильное приливное воздействие, либо столкновение двух галактик с последующим слиянием. Другой возможностью является доминирование однорукавной спирали $m=1$ в соответствии с механизмом swing amplification [259]. Условия для развития однорукавной волны в линейном приближении рассматривались в работах Занга [909], Эванса и Рида [388, 389] и результаты линейного анализа подтвердились в численных моделях $N\!$-тел [783].

Для обозначения различных асимметричных проявлений термин ``lopsided-галактики''^3.15 (он используется во всех цитировавшихся выше работах) можно считать устоявшимся, и в данном параграфе мы будем обсуждать в первую очередь смещение бара относительно центра дисковой компоненты. Рассмотрим условия, при которых возможно формирование смещенных баров в процессе развития гравитационной неустойчивости глобальной бар-моды в изолированной первоначально осесимметричной системе [63, 542]. В основе физического механизма смещения бара лежит нелинейная стадия совместного развития бар-моды и однорукавной гармоники с азимутальным числом $m=1$. С увеличением массы и/или уменьшением шкалы балджа условия для смещения бара ухудшаются. Наиболее эффективно смещение бара происходит в случае маломассивного гало, пространственная шкала у которого существенно превосходит радиальную шкалу диска.

3.7.1 Формирование изолированных lopsided-галактик

Одним из механизмов образования бара является развитие гравитационной неустойчивости моды $m=2$ в недостаточно (для устойчивости) горячем диске, когда дисперсия радиальных скоростей звезд $c_r(r)$ не превосходит критического значения, которое определяется параметрами дисковой и сфероидальной подсистем (п. 3.2.2).

Модели без сфероидальной подсистемы. В данном пункте рассмотрим изолированный самогравитирующий диск без учета сфероидальной подсистемы. И хотя у реальных галактик наличие гало является, по-видимому, обязательным компонентом (см., например, § 3.4, 3.5), на этом примере обсудим некоторые особенности формирования бара.

Можно выделить два класса моделей, различающиеся начальной толщиной диска. В основе этих двух моделей лежат разные сценарии формирования галактик. В первом случае в результате коллапса протогалактического облака первоначально образуется квазистационарный достаточно холодный газовый диск, в котором далее возникает звездное население. Во втором случае происходит быстрое образование толстого звездного диска в ходе сжатия газа к плоскости галактики, и звезды изначально имеют более высокую дисперсию вертикальных скоростей.

Figure: Модель первоначально холодного ( $Q_T(r\le 2L)=0,7$) тонкого ( $\Delta /L=~0,082$) диска без сфероидальной подсистемы с $N=5\cdot 10^5$. Здесь (а) - зависимость от времени интегральных амплитуд фурье-гармоник $\hat{A}$ для различных азимутальных чисел $m$; (б) - зависимость от времени координат ($\bullet$ -- $x$-координата, $+$ -- $y$-координата) центра бара. Центр системы координат совпадает с центром тяжести всего диска

=0.999

Модели с тонким начальным диском. Если в начальный момент времени центральная область диска является достаточно холодной ( $Q_T(r\le~2L)=0,7$) и тонкой $c_z/c_r\lee~0,4$ (дисперсия вертикальных скоростей связана с вертикальной шкалой соотношением $\Delta\simeq c_z^2/\pi G\sigma$ в (3.13)), то наряду с ростом двухрукавной моды, приводящей к образованию бара, формируется однорукавное возмущение значительной амплитуды (рис. 3.53 $\!\!$а). Интегральная амплитуда фурье-гармоники $\hat{A}(m=1)$ доминирует на протяжении всего расчета, за исключением самой начальной стадии ($t\lee 4$). Вычисление величин (3.23), (3.24) проводилось в системе координат центра тяжести диска, смещение которого к моменту времени $t=10$ не превышало в плоскости диска $(x,y)$ значения $\vert\vec{\xi}_{disc}\vert< 0,002$, что характеризует точность интегрирования уравнений движения. Ярко выраженная периодичность $\hat{A}(m=1,t)$, а также гармоник с номерами $m=3,4,5,6$, является следствием вращения бара относительно своего центра, который не совпадает с центром диска, с периодом .

Figure: Изолинии поверхностной плотности в модели без сфероидальной подсистемы, показанной на рис. 3.53, в разные моменты времени. Кинематический центр и центр тяжести всего диска находятся в центре координат (координатные оси изображены пунктирными линиями). В квазистационарном состоянии в области $r<1$ остается $\simeq 70$% массы диска

=0.999

Таким образом, в процессе своего формирования из осесимметричной системы бар оказывается смещенным относительно центра тяжести всего диска. На рис. 3.53$\!$б показана динамика центра бара . Формирование квазистационарного бара заканчивается к моменту времени $\!t\simeq 10$ (динамическое время в моделях равно $T_0=2\pi \sqrt{R^3/GM_d}=~2\pi\!$). После этого движение центра бара в инерциальной системе координат практически прекращается (см. рис. 3.53$\!$б, 3.54). В данном расчете смещение центра бара относительно центра массы всей дисковой компоненты составило $\!\xi_{bar}=\sqrt{x_{bar}^2+y_{bar}^2}=0,\!17=0,\!7L\!$. Кинематический центр всего диска совпадает с центром его инерции.

В изолированном диске его центр тяжести $\vec{\xi}_{disk}$ и кинематический центр $\vec{\xi}_{kc}$ не должны меняться в процессе эволюции системы. Поэтому проверка выполнения этих условий может являться тестом при построении численных моделей. При вычислении гравитационной силы методом TREEcode при $\Theta=1$ к концу расчета ($\simeq 10$ периодов вращения) из-за численных эффектов центр инерции диска смещается на величину $\xi_{disk}\simeq 0,03\ll \xi_{bar}$ ($\xi_{disk}$ уменьшается при выборе меньших $\Theta$). Для проверки степени влияния данного эффекта на эволюцию системы удобно использовать модели, в которых гравитационная сила вычисляется прямым суммированием вкладов от всех частиц (метод  PP -- см. п. 3.1.1). Метод PP позволяет существенно уменьшить величину смещения дисковой компоненты $\vec{\xi}_{disc}$ (то есть фактически ошибку, обусловленную численным решением) до значений $\xi_{disk}< 10^{-5}$. При этом все результаты, связанные со смещением бара в моделях TREEcode, остаются справедливыми.

Величина смещения бара уменьшается с ростом начальной дисперсии скоростей $c_r\!$. В более горячем в начальный момент времени диске скорость образования бара замедляется (в очень горячей системе бар не образуется, см. п. 3.2.2) и одновременно ухудшаются условия для роста моды $m=1$. В результате уже при $Q_T(r\le 2L)\ge 1,05$ смещение бара оказывается незначительным.

Отметим, что в случае более горячего в момент $t=0$ диска многорукавные волны () имеют заметно меньшую амплитуду по сравнению с . В обратном предельном случае очень холодного диска () помимо основного бара могут формироваться еще одно или несколько более мелкомасштабных возмущений на периферии диска, поскольку джинсовский масштаб оказывается очень мал $\varrho_J\ll L$. Эти области повышенной плотности являются гравитационно связанными на протяжении нескольких оборотов вращения системы (см. максимумы плотности на рис. 3.54, помимо бара -- см. значок $\star$ в момент времени $t=4$). С ростом начальной дисперсии скоростей $c_r$ остается только центральная бар-структура. В случае очень холодного диска формирование бара сопровождается сильным смещением относительно динамического центра. Величина смещения $\xi_{bar}$ может превышать начальную радиальную шкалу диска $L=0,25$.

Figure: Начальная стадия эволюции в модели первоначально толстого диска ( $\Delta/L\simeq 0,\!25$) без сфероидальной подсистемы ($N=10^6$). Здесь (а) - изолинии логарифма поверхностной плотности в разные моменты времени. Величина смещения бара приблизительно в два раза меньше, чем в случае модели на рис. 3.53, 3.54; (б) - зависимости от времени интегральных амплитуд фурье-гармоник (3.24) для различных азимутальных чисел $m=1,2,3,4,5,6$

=0.999

Модели с толстым начальным диском. Если в начальный момент времени диск является более толстым, то его эволюция меняется. Даже если он относительно холодный в плоскости ($x,y$), что допускает формирование бар-моды, то смещение бара уменьшается (рис. 3.55), что проявляется в уменьшении амплитуды гармоники $m=1$ и ее более медленном росте по сравнению с моделью, в которой диск является более тонким в начальный момент времени (рис. 3.55$\!$б).

Смещение бара практически исчезает начиная со значений вертикальной шкалы $\Delta/L\gee 0,4$ в отсутствие гало. Толстые диски являются гравитационно более устойчивыми (см. (3.35)). Поэтому характерные времена образования любых структур, обусловленных самогравитацией, увеличиваются с ростом толщины диска, а амплитуда этих образований уменьшается. Толщина диска определяется дисперсией $z$-скоростей $c_z$. Таким образом, существуют критические начальные значения дисперсии радиальных и вертикальных скоростей, которые допускают заметное смещение бара.

Модели с балджем. Рассмотрим эволюцию диска с учетом дополнительного гравитационного поля стационарного балджа, который характеризуется относительной массой $M_b/M_d$ и радиальной шкалой . Маломассивный балдж ($M_b/M_d=0,\!1$, $b/L=0,\!2$) в отсутствие гало на начальной стадии эволюции допускает развитие как бар-моды, так и однорукавной гармоники. В этом случае центр бара близок к центру балджа (причина связана со статичностью балджа), но смещен относительно кинематического центра и центра тяжести дисковой компоненты. Поле скоростей в области бара имеет сильно несимметричный вид.

Генерация моды с азимутальным номером $m=1$ возможна и в случае более массивного балджа (), если он не является очень концентрированным. При малой шкале балджа условия для развития однорукавных возмущений исчезают.

При наличии балджа смещение бара оказывается при прочих равных условиях меньше, и оно со временем медленно уменьшается из-за взаимодействия асимметричного диска со статичным балджем. Этот эффект аналогичен влиянию гало (см. ниже), однако в случае балджа он более резко выражен. Уменьшение величины $\xi_{bar}$ со временем полностью обусловлено взаимодействием жесткой сфероидальной компоненты с баром. Характерное время этого процесса составляет несколько периодов обращения внешнего края диска. Учет ``живого'' балджа может заметно изменить динамику этого процесса, сохраняя принципиальный вывод об уменьшении смещения бара со временем.

По-видимому, стабилизация однорукавных возмущений балджем и уменьшение смещения бара со временем с учетом гравитационного поля балджа является причиной того, что смещение баров наблюдается преимущественно у галактик поздних типов, начиная с морфологического типа $Scd$, у которых, как правило, отсутствуют сколько-нибудь заметные центральные сферические подсистемы.

Эволюция диска в учетом гало. Масса гало в пределах оптически наблюдаемого диска может превышать массу дисковой компоненты (см. § 3.4, 3.5). Поэтому рассмотрим более реалистичные модели, включающие гало в соответствии с (3.3).

Figure: Модель с гало: масса $M_h=M_d$, шкала $a=2L$, число частиц $N=2,5\cdot 10^5$. Показаны изолинии поверхностной плотности в разные моменты времени

=0.37

Вывод о том, что в случае первоначально тонкого холодного диска смещение бара $\xi_{bar}$ оказывается возможным, сохраняется и при учете гало. В таких моделях с начальным $Q_T(r\le 2L)=0,\!6\div 0,\!8$, как и в случае без гало, характерной особенностью эволюционирующего диска является возможность нарастания до больших амплитуд гармоники $m=1$, что может на начальной стадии приводить к смещению бара. Данные эффекты наиболее сильны при достаточно рыхлом гало, шкала $a$ у которого в $2~\div~4$ раза превосходит радиальную шкалу диска. В этом случае динамика диска в области $r\le 2L$ определяется в первую очередь распределением массы в дисковой компоненте. На рис. 3.56 показана эволюция диска в модели с $M_h=M_d$, $a=2L$. Как и в случае без гало, на начальной стадии происходит формирование асимметричного диска, в котором бар оказывается смещенным относительно центра тяжести и кинематического центра всего диска. Затем из-за статичности сфероидальной подсистемы смещение бара уменьшается. При меньших значениях шкалы гало $a$ смещение бара уменьшается и динамика системы оказывается похожа на случай модели с концентрированным балджем без гало.

Если рассмотренный механизм является ответственным за формирование, по крайней мере, части lopsided-галактик, то у таких галактик поздних морфологических типов внутри оптического радиуса в среднем относительная масса гало меньше, чем у симметричных галактик.

Учет динамики балджа и гало. Учтем в первом приближении движение сфероидальной подсистемы. Считаем, что балдж или гало определяются законом плотности соответственно (3.5) или (3.3), но положение центра жесткой подсистемы описывается дополнительным уравнением движения в системе уравнений (3.2). В такой модели c нестационарным гало или балджем центр масс всей моделируемой системы остается неподвижным. Формирование бара в холодном диске качественно не отличается от случая неподвижной сфероидальной подсистемы (рис. 3.57). Однако возникшее смещение бара относительно центра диска сохраняется. Причем расстояние между центрами диска и гало в несколько раз меньше, чем $\xi_{bar}=\sqrt{x_{bar}^2+y_{bar}^2}$.

Звездно-газовые модели. Характерной особенностью галактик позднего типа является большая относительная доля газа по сравнению с объектами раннего типа. Поэтому рассмотрим принципиальное влияние газовой компоненты на эффект смещения баров и в целом появление асимметрии в структуре диска [542].

Figure: Модель с нестационарным гало ($M_h=M_d$, $a=2L$): показаны изолинии плотности $\sigma$ и динамика координат центра бара (а). Модель звездно-газового диска: изолинии поверхностной плотности газовой (б) и звездной компоненты (в). Смещение центра бара относительно центра диска и степень асимметрии спиральной структуры усиливаются с увеличением относительной массы газа

=0.999

В качестве начального состояния для звездной компоненты выберем диск, близкий к границе гравитационной устойчивости в отсутствие газа. Таким образом, начальные распределения дисперсий скоростей таковы, что без учета газовой компоненты амплитуда однорукавной гармоники $m=1$ очень мала, и формирование асимметричного диска не происходит, хотя начальное состояние и допускает медленное образование бара. В массивной холодной газовой подсистеме возможно формирование гармоники $m=1$, которая на нелинейной стадии приводит к асимметрии и звездного диска. На рис. 3.57 показаны результаты такого расчета в модели с $M_{gas}=0,\!47\,M_d$ в пределах $r\le 4L$ ($M_h=M_d$, $a=1,\!6\,L$). Механизм формирования асимметричных (lopsided) галактик в результате гравитационной неустойчивости возмущений с азимутальным числом $m=1$ и взаимодействия на нелинейной стадии однорукавной моды с бар-модой в случае маломассивного рыхлого гало оказывается более эффективным при наличии холодной газовой компоненты. Асимметричность диска усиливается с ростом относительной массы газа.

3.7.2 Динамическая модель Большого Магелланова Облака

Классическим примером галактики переходного типа от спиралей $Sc$ к неправильным является Большое Магелланово Облако (БМО). Многие объекты, относящиеся не только к типу $Sm$, но и $Sd$, часто называют галактиками Магелланова типа [578, 707]. Поэтому в продолжение рассмотренных выше вопросов, более подробно остановимся на БМО. Для этого построим серию динамических моделей БМО и, согласуя их с данными наблюдений, определим некоторые ненаблюдаемые параметры и обсудим причины формирования характерных особенностей структуры БМО [63].

Основные данные наблюдений. Исследования последних лет, по-видимому, позволяют говорить о более сложной, чем это было принято считать, морфологии БМО. По сравнению с оптическим изображением, в линии $HI$ галактика более симметрична и похожа на классические дисковые галактики [544]. Газовый диск прослеживается до радиуса 7 кпк ^3.16. Отдельные звезды удается обнаружить примерно до тех же расстояний. Измерения кривых вращения по наблюдениям $HI$ и ярчайших звезд позволяют построить модели распределения вещества в галактике. При этом данные по фотометрии и кинематике звезд и наличие бара существенно ограничивают неопределенность свободных параметров, описывающих радиальные зависимости плотности вещества в диске и гало.

Figure: Кривые вращения для БМО: ( а) -  из работы Софю [818],  1 -- из данных наблюдений,  2 -- сглаженная кривая вращения; ( б) -  из работы Кима и др. [544]

=0.999

На больших расстояниях от центра БМО наблюдаемые скорости вращения диска (как по газу, так и по звездам) лежат в пределах 68-80 км/с без признаков падения кривой вращения с радиусом. Особый интерес представляет внутренняя часть диска. Софю [818] проанализировал заново данные Кима и др. [544] и построил кривую вращения $HI$, отличающуюся в центральной области ($r\lee 2$ кпк) от кривой вращения $V_{gas}^{K}$ Кима и др. [544] существенно более высоким радиальным градиентом скорости вращения (рис. 3.58). Причина расхождения обусловлена в первую очередь разным выбором кинематического центра. Для того чтобы объяснить высокий градиент скорости газа вблизи выбранного центра, Софю был вынужден ввести в модель темный балдж, который в основном определяет движение в области $r\lee 1$ кпк. Второй особенностью является маленькая радиальная шкала поверхностной плотности в модели Софи, равная 1 кпк, что существенно меньше обычно принимаемого для диска БМО значения экспоненциальной шкалы $L=1,\!6$ кпк. В то же время для объяснения кривой вращения, представленной в работе Кима и др. [544], массивный балдж не требуется. Чтобы изучить возможность существования предложенного темного массивного балджа в БМО, нами были построены две серии динамических моделей для каждой из кривых вращения.

Распределение вещества в дисковой компоненте. Будем использовать обычно принимаемые значения расстояния до БМО (50,1 кпк) и угла наклона ($i=33^\circ$) [569]. Радиальные зависимости поверхностной яркости диска, долгопериодических переменных, RR Lyrae и углеродных звезд хорошо описываются экспоненциальным законом с $L=1,\!6$ кпк (см. работу [244] и ссылки в ней).

Бар. В центральной части БМО выделяется оптический бар. Его длина составляет около 3,3 кпк. Отличительной чертой центральной области БМО является несовпадение кинематического центра диска и центра бара [435] ^3.17.

Данные наблюдений свидетельствуют, что последние $(2\div 4)\cdot 10^{9}$ лет в центральной области галактики активного звездообразования, по-видимому, не происходило [433]. В работе [491] обнаружено, что существенная часть звезд имеет возраст старше 4 млрд лет, причем сделан вывод, что независимо от выбора модели область бара содержит относительно больше старых звезд, чем внешние области галактики. Исследования возрастов кластеров, распределенных в баре и диске, показали их различие. История формирования звездного населения в баре отличается от других областей, и в работе [39] сделан вывод, что бар в БМО сформировался $(2\div 6)\cdot 10^9$ лет назад. Поэтому будем считать, что бар в БМО является устойчивой структурной особенностью -- по разным данным его возраст оценивается в $2\div 9$ млрд лет [39, 251, 491]. Таким образом, даже если изначально бар возник не в результате развития неустойчивости глобальной бар-моды, а вследствие приливного взаимодействия или действия иного механизма, то условия в галактике должны быть такими, чтобы время существования бара могло быть не менее нескольких миллиардов лет.

Figure: Для модели с $\mu = 1,\!9$ и $L=1,\!6$ кпк показаны: (а) - вклад в круговую скорость галактики (сплошная толстая линия) от диска, гало, балджа и ядра; (б) - радиальное распределение наблюдаемых и модельных скоростей. Условные обозначения: + -- скорость вращения $HI$; $\star$ -- скорость вращения звезд (большие звездочки -- [243], маленькие звездочки -- [569]); o -- наблюдаемая дисперсия скоростей звезд; $\bullet$ -- модельные оценки скорости вращения звезд; ${\diamond }$ -- модельные оценки дисперсии скоростей звезд в проекции на луч зрения; (в) - то же для модели с $\mu = 1,\!1$ и $L=1,\!6$ кпк; ( г) - то же для максимального диска для $V^{S}_{gas}(r)$ c $L=1$ кпк

=0.999

Кинематика газа и звезд. За основу построения динамических моделей мы взяли кривые вращения газа по работам Софи [818] ( $V_{gas}^{S}(r)$) и Ким и др. [544] ( $V_{gas}^{K}(r)$) (см. рис. 3.58$\!$а,$\!$б, толстые линии и рис. 3.59, 3.60). Показаны также скорости вращения $V_\star$ и дисперсии скоростей $c_{obs}$ звезд. Сглаженная кривая вращения газа принималась в качестве кривой круговой скорости вращения $V_c(r)$.

Кинематика звезд диска в БМО изучена достаточно хорошо. Кюнкель и др. [569] по 759 углеродным звездам построили кривую вращения в области от 3 до 12 кпк. Мы ее используем с учетом угла наклона $i=33^\circ$ (см. рис. 3.59, 3.60). Дисперсия скоростей этих звезд вдоль радиуса слабо меняется и составляет $c_{obs}=12\div 16$ км/с, что, по-мнению авторов данной работы, указывает на их относительно молодой возраст. В дополнение к этим данным на рис. 3.59, 3.60 показаны радиальные зависимости скорости вращения и дисперсии скоростей звезд диска, полученные в работе [244].

Анализ кинематики [450] более пятисот углеродных звезд позволил выявить наряду с более молодым населением, у которого дисперсия скоростей около 8 км/с, и старую дисковую компоненту с дисперсией скоростей $\simeq 22$ км/с. В работе [910] по 190 VRC (Vertical Red Clump) звездам определена дисперсия скоростей $18,4~\pm~2,8$ km/s. Данные по кинематике планетарных туманностей в работе [618] $c_{obs}=19,1~\pm~1$ км/с согласуются с вышеприведенными результатами. Движение 975 углеродных звезд позволило оценить максимальную круговую скорость вращения $\simeq 80$ км/с на расстоянии 3,4 кпк от центра и дисперсию радиальных скоростей дисковой компоненты $c_r=28\pm 14$ км/с [243].

Figure: Сравнение наблюдаемых и модельных параметров для кривой вращения $V^{K}_{gas}(r)$ для модели с массивным гало (a) и максимального диска ($\mu = 0,\!74$) (б). Условные обозначения -- те же, что для рис. 3.59

=0.999

Отметим, что радиальная зависимость скорости вращения и дисперсии скоростей звезд становится несколько иной, если изменить положение кинематического центра, следуя работе Софю [818]. Однако, поскольку дисперсия скоростей $c_{obs}$ очень слабо зависит от радиальной координаты, ход дисперсии с радиусом остается практически тем же, а изменения звездной кривой вращения $V_\star$ возможны только для центральной области $r\lee 1$ кпк. По этой причине, в частности, кинематические параметры звезд вблизи центра БМО следует признать наименее надежными.

3.7.3 Результаты динамического моделирования БМО

Целью динамического моделирования является получение ограничений, позволяющих производить выбор между кривыми вращения Кима и др. [544] и Софю [818] и, тем самым, проверить возможность существования в БМО темного балджа [63]. Основной вывод заключается в том, что кривая вращения в работе [544] (см. рис. 3.58$\!$б) лучше согласуется с совокупностью наблюдательных данных для БМО, и присутствие значительной темной массы внутри БМО не требуется.

Обсудим динамические модели с разными распределениями вещества в подсистемах. Поскольку в работе Софю для объяснения кривой вращения $V_{gas}^{S}$ рассматривалось распределение вещества, отличное от обычно используемого распределения яркости, следует проанализировать динамические модели с различным значением радиальной шкалы диска $L=1\div 1,6$ кпк, определяя ее в качестве свободного параметра.

1) Динамические модели с кривой вращения $V_{gas}^{S}$. Рассмотрим случай кривой вращения $V_{gas}^{S}(r)$ с $L=1,\!6$ кпк и массивным гало . Для объяснения центрального максимума на кривой вращения модель включает наряду с массивным балджем ( ) и компактное ядро с . На рис. 3.59$\!$а показаны вклады от различных компонент в круговую скорость вращения $V_c(r)$, а на рис. 3.59$\!$б приведены распределения наблюдаемых величин $c_{obs}$, $V_{gas}$, $V_\star$ и соответствующих модельных величин $c^s$, $V_c$ и $V\!$. На периферии галактики стационарное состояние диска достигается при очень маленьких значениях дисперсии скоростей звезд -- в области $r>3L$ дисперсия радиальных скоростей $c_r=10\div 14$ км/с, что сравнимо с дисперсией скоростей газа. Эта модель предполагает значительный запас устойчивости: $c^{s}<c_{obs}$ в галактике, где $c^s$ и $c_{obs}$ -- дисперсии вдоль луча зрения по (3.41). Скорость вращения звезд $V$ в рассматриваемой модели сравнима с круговой скоростью $V_c$, и в центральной области значительно превосходит наблюдаемые скорости вращения звезд $V_\star$, что является недостатком модели. Увеличение $\mu$ приводит к еще большему расхождению с наблюдаемой дисперсией скоростей.

Кроме того, для моделей с высоким $\mu$ долгоживущий бар не удалось сформировать ни при каких начальных распределениях дисперсии скоростей звезд. Совместное действие двух факторов -- наличия относительно массивного гало и концентрированного ядра, приводит к тому, что в процессе разогрева системы центральная перемычка оказывается недолгоживущей, о чем свидетельствует уменьшение со временем амплитуды всех фурье-гармоник и в том числе моды $m=2$ (п. 3.7.1). Если даже задать в качестве начальных условий очень холодный диск, у которого в значительном интервале радиуса параметр Тоомре $Q_T<0,\!5$, то после бурного разогрева и формирования на начальном этапе бароподобной структуры все равно устанавливается осесимметричное распределение плотности после $\sim 12$ периодов обращения по внешнему краю диска.

Альтернативной моделью для выбранного значения $L$ является модель максимального диска (ММД), для которой $\mu = 1,\!1$ (рис. 3.59$\!$в). Дисперсия скоростей $c^s$ в этом случае на периферии диска лучше согласуется с наблюдаемым распределением. Однако в центральной зоне дисперсия скоростей вдоль луча зрения $c^s \simeq 40~\div~50$ км/с, что противоречит наблюдениям. Формирование бара в случае первоначально холодного диска оказывается возможным, но он также оказывается короткоживущим. После окончательного формирования бара ( $t\simeq 5\div 6$) начинается его разрушение из-за рассеяния на концентрированном ядре. В результате оказывается, что время его жизни ограничено $\sim (2\div 3)\,\cdot 10^9$ лет, что лишь незначительно превышает нижнюю оценку возраста бара по анализу его звездного состава. Причина того, что в предыдущем случае ($\mu = 1,\!9$) время жизни бара оказывается меньше, чем в случае $\mu = 1,\!1$, помимо различия в массе гало, обусловлена тем, что диск в случае ММД является более толстым. Поэтому компактное ядро, характерный радиус которого существенно меньше полученной вертикальной шкалы диска $360$ пк, не обеспечивает быстрого разрушения бар-моды, и процесс диссипации бара затягивается на $\sim 10$ оборотов бара.

Модели с более концентрированным диском ($L=1$ кпк) и той же кривой вращения $V_{gas}^{S}$ еще хуже согласуются с наблюдаемой дисперсией скоростей: практически весь диск обладает большим запасом устойчивости, в то время как в самом центре выполняется обратное условие $c_{obs}<c^{s}$.

2) Динамические модели с кривой вращения $V_{gas}^{K}$. Опишем теперь результаты динамического моделирования с кривой вращения $V_{gas}^{K}(r)$, для интерпретации которой не требуется балджа и ядра.

В модели с гало для дисперсии скоростей звезд за исключением самого центра выполняется условие $c^s < c_{obs}$ и достигается удовлетворительное согласие со скоростью вращения звезд в области $r>1,\!5L$ (рис. 3.60$\!$а). В модели максимального диска ($\mu=0,\!7$) для $V_{gas}^{K}(r)$ удается получить наилучшее совпадение между результатами моделирования и наблюдениями дисперсии скоростей звезд и скоростью их вращения (рис. 3.60$\!$б). Этот результат подтверждает вывод о малой массе гало у БМО, впервые сделанный в работе [50] по данным о кинематике шаровых скоплений, принадлежащих диску, исходя из условия пороговой гравитационной устойчивости диска.

В модели с кривой вращения $V_{gas}^K(r)$, если начальный диск не очень горячий, всегда формируется долгоживужий бар, который существует $\simeq 4~\cdot~10^9$ лет. Угловая скорость вращения бара в модели составляет $\Omega_{bar}=23$ км/(с$\,\cdot\,$кпк).

Отличительной особенностью формирования бар-структуры в случае моделей с $V_{gas}^{K}(r)$ является при определенных условиях большая амплитуда первой моды $m=1$, которая остается значительной на протяжении всей эволюции и характеризует нарушение симметрии бара относительно центра галактики. Последнее хорошо согласуется с наблюдаемым смещением кинематического центра относительно центра бара. Подробно феномен смещения бара рассматривался выше в п. 3.7.1. Но особо подчеркнем, что наиболее благоприятные условия возникают в случае значительного преобладания массы диска над гало практически во всем диске.

Figure: Радиальные зависимости масс, заключенных внутри радиуса $r$, для дисковой и сферической подсистем в случае моделей с кривыми вращения $V^{S}_{gas}(r)$ (а), $V^{K}_{gas}(r)$ (б). Толстая линия -- полная масса, тонкая линия -- дисковая компонента, штриховая -- сфероидальная подсистема

=0.34

Сказанное выше иллюстрируется на рис. 3.61, где приведены радиальные зависимости масс дисковой и сферической подсистемы внутри данного радиуса БМО для различных моделей. В случае кривой вращения $V_{gas}^{S}(r)$ масса диска доминирует в области 1,5кпк$\le r \le 6$ кпк (рис. 3.61а). Модель, базирующаяся на кривой вращения $V_{gas}^{K}(r)$, допускает, что в дисковом компоненте сосредоточена большая часть массы галактики на всех радиусах (рис. 3.61б). При этом внутри области $r<2L=3,\!2$ кпк масса гало составляет всего 20 % от массы диска, то есть динамическая роль темной массы мала.

Построить модель с менее массивным гало ($\mu < 0,\!7$), которая бы согласовывалось с $V_{gas}$ за радиусом $r>4$ кпк, не удается в рамках рассматриваемой модели изотермического гало (3.3). Впрочем, если наблюдаемый рост кривой $V_{gas}$ на периферии диска является результатом действия приливного влияния, а не роста круговой скорости, то масса гало может оказаться еще более низкой.

Выводы. Укажем на те особенности моделей с кривой вращения $V_{gas}^{S}(r)$ (с темным балджем), которые делают модели с $V_{gas}^{K}(r)$ (без темного балджа) более адекватными наблюдениям:

a) модели с $V_{gas}^{S}(r)$ не объясняют наблюдаемую радиальную зависимость скоростей звезд во внутренней области галактики $r<2L$;

б) эти модели либо не допускают формирование бар-моды, либо время жизни бара оказывается недостаточно большим;

в) амплитуда однорукавной моды $m=1$, характеризующая асимметрию в распределении вещества, в моделях с массивным балджем очень мала (на уровне шума) на протяжении всей эволюции системы, в отличие от моделей с $V_{gas}^{K}(r)$, для которой при формировании бара мода $m=1$ обладает большой амплитудой, и на протяжении всей эволюции системы ее амплитуда лишь ненамного уступает амплитуде второй моды. Это обстоятельство позволяет естественно объяснить наблюдаемое смещение кинематического центра БМО относительно центра бара даже без учета приливных эффектов;

г) во внутренней области диска ($r<L$) в модели с $V_{gas}^{S}(r)$ для устойчивости диска требуется дисперсия скоростей звезд, превышающая 40 км/с (в проекции на луч зрения), что значительно превосходит наблюдаемую величину $c_{obs}$. При этом модели с небольшой радиальной шкалой диска $L\simeq 1$ кпк хуже согласуются с наблюдаемыми распределениями скорости вращения и дисперсии скоростей звезд, чем в случае с $L=1,\!6$ кпк.

Таким образом, кривая вращения Ким и др. [544] представляется более предпочтительной. Поэтому предположение о существовании темного балджа в БМО нами не подтверждается.

Построенные динамические модели допускают применимость модели максимального диска для БМО, при этом масса гало в пределах $r<4L=6,\!4$ кпк составляет около 70 % от массы дисковой компоненты. Наблюдаемая дисперсия скоростей на периферии диска $c_{obs}(r\ge 3) \simeq~16\div 20$ км/с [569,244, 243] означает, что эта область имеет запас устойчивости даже в модели максимального диска. Следует подчеркнуть, что построенные динамические модели не исключают существования более массивного гало с $\mu \simeq 1\div 2$, однако в этом случае дисперсия скоростей звездного диска должна быть обусловлена не динамическим нагревом в результате гравитационной неустойчивости, а иными факторами.

3.8 Сложные несимметричные структуры в центре галактик

3.8.1 Проблема двойных баров

Во многих галактиках центральная часть выглядит как сложная система, состоящая из нескольких вложенных друг в друга компонент (бары, диски, кольца, двойные ядра). По-видимому, первым объектом, заподозренным в наличии так называемого ``двойного бара'', стала галактика NGC 1291 [873]. Особый интерес к мелкомасштабным несимметричным структурам в центре дисков связан с изучением феномена ядерной галактической активности. Важной проблемой является выявление механизмов, обеспечивающих приток газа в самый центр к сверхмассивной черной дыре ($\!\!\lee10$ пк). Считается, что двойные бары могут поставлять газ в активное ядро [797].

Список кандидатов галактик с двойными барами включает более 70 объектов [645]. Почти во всех случаях основным аргументом наличия второго ^3.18 внутреннего бара являются фотометрические данные. Разделение внутренних структур на двойные бары, внутренние диски и ядерные кольца в рамках фотометрического подхода [386], по-видимому, неоднозначно. Анализ кинематики центральных областей этих галактик во многих случаях не подтверждает выводы из фотометрии и свидетельствует не в пользу большой распространенности двойных баров [118, 645, 646]. Рассмотрим характерные особенности кинематики структур типа ``двойные бары'' (скорости и дисперсии скоростей) в рамках самосогласованных динамических моделей. Важной проблемой двойных баров является также вопрос о динамической устойчивости такого рода систем.

3.8.2 Распределение параметров в области двойного бара

Figure: Изолинии логарифма поверхностной плотности в разные моменты времени в модели с $M_h=M_d$, $M_b=0,\!6M_d$, $b=0,\!16L$, . Показана только центральная область диска $r\le 2L$

=0.999

Опишем результаты численного моделирования звездного диска, допускающего формирование бара [211, 542]. Образование внутренней бароподобной структуры в численных моделях оказывается возможным при наличии достаточно массивного (но не концентрированного!) балджа. На рис. 3.62 показаны распределения $\lg(\sigma)$ в разные моменты времени в модели, в которой на определенных этапах возникают структуры типа двойных баров.

На начальном этапе (1-3) образуется двухспиральная волна, а в центре - маленькая бароподобная структура с большой полуосью $\simeq 0,\!3L$. Затем формируется внешний бар (см. рис. 3.62,$\!$4, 5), перпендикулярный внутреннему. Две спиральные волны от внутреннего бара ``вписаны'' во внешний бар. Такая структура оказывается недолгоживущей, происходит перестройка (см. рис. 3.62,$\!$6), в результате которой вновь образуется ``двойной бар'' (7, 8, 9). В новой конфигурации размеры баров оказываются больше, особенно внешней перемычки. Однако со временем происходит разрушение двойного бара (см. рис. 3.62,$\!$10, 11) и остается один глобальный бар (12).

Заметим, что при формировании и разрушении (см., например, рис. 3.62,$\!$7) внутреннего бара наблюдаются короткоживущие структуры, напоминающие ``неперпендикулярные двойные бары''^3.19. При этом в центральной области возникают лидирующие спиральные волны, а от концов внешнего бара отходят отстающие спирали.

Figure: Изолинии дисперсий скоростей $c_r$, $c_\varphi$, $c_z$ (вверху), радиальной (сплошная линия -- $U=0$) и азимутальной ($V$) компонент скорости на стадии двойного бара

=0.999

Рассмотрим кинематику центральной области диска ($r\le 2L$) на стадии двойного бара. Изолинии дисперсии радиальных скоростей $c_r$ имеют овальную структуру (рис. 3.63), сонаправленную с большой осью внешнего бара. В области, которую занимает внутренний бар, обнаруживаем два максимума $c_r$. Однако эта характерная особенность не является признаком внутреннего бара, поскольку сохраняется после разрушения внутренней перемычки. Распределение дисперсии вертикальных скоростей на стадии двойного бара сильнее отличается от случая одиночного бара. И только дисперсия азимутальных скоростей более ярко выделяет наличие внутреннего бара.

Важным свидетельством наличия внутреннего бара является поле скоростей. На рис. 3.63 показаны распределения азимутальной компоненты скорости $V$ и радиальной $U$. На стадии двойного бара имеется вытянутость изолиний $V$ вдоль внутренней перемычки. Радиальная скорость обнаруживает характерную четырехсекторную структуру как для внешнего бара, так и для внутреннего. Линия $U=0$ проходит вдоль большой и малой осей бара.

Анализ вертикального распределения вещества в диске говорит об отсутствии гидростатического равновесия (см. (3.12)) на стадии двойного бара. Причина связана с явлением изгиба бара при его формировании. Изгибная неустойчивость бара представляется одним из факторов, приводящих к разрушению системы двойного бара.

Итак, формирование структур типа двойного бара возможно в процессе нелинейной стадии формирования глобального бара при наличии достаточно массивного $M_b\gee 0,\!3M_d$ и ``рыхлого'' балджа $b\simeq (0,\!12\div~0,\!28)\,L$. Возникновение внутренней перемычки в моделях наблюдается, если в начальный момент: 1) диск тонкий ( $z_0/L=0,\!04\div 0,\!1$); 2) радиальный профиль $c_r$ близок к зависимости на рис. 3.17,$\!$5, то есть диск достаточно горячий. В этом случае рост возмущений начинается в самой центральной области диска (см. рис. 3.62,$\!$1, 2, 3). Если же диск холодный ($Q_T < 1$), то формируется система транзиентных спиралей и выживает бар-мода без стадии внутренней перемычки.

3.8.3 К вопросу об устойчивости двойных баров

Важнейшей проблемой двойных баров является вопрос о динамической устойчивости такого рода систем. Выше отмечено, что длительность фазы ``двойного бара'' невелика, и одной из причин исчезновения внутренней перемычки является начало релаксационных процессов в вертикальном направлении -- внешними проявлениями являются разогрев и утолщение системы. На начальной стадии формирования бара изолинии вертикальной шкалы диска $\Delta$ повторяют распределение плотности. Но вертикальный разогрев разрушает орбиты, вытянутые вдоль малой оси внешнего бара, что приводит к разрушению внутренней структуры.

Figure: (а) - распределение вертикального смещения центра тяжести $\zeta$ в плоскости диска. Толстая линия -- уровень $\zeta =0$; (б) - показана только область бара; (в) - профиль вертикального смещения вдоль бара. Стрелки показывают положения концов бара

=0.999

Формирование бара в тонком диске сопровождается изгибной неустойчивостью, которая в конечном счете приводит к утолщению всего диска (см. § 3.5). Рис. 3.64 демонстрирует типичный изгиб бара на нелинейной стадии, когда в диске имеется однорукавное изгибное возмущение (рис. 3.64$\!$а). Длина волны коробления бара чуть больше его длины (рис. 3.64$\!$б). Вдоль большой оси бара, как правило, укладывается 1-2 длины изгибной волны. На изгиб бара накладываются спиральные изгибные моды с азимутальным числом , изгибающие весь диск.

После стабилизации изгибной неустойчивости, когда система прекращает свой разогрев и в плоскости диска и в вертикальном направлении, внутренняя перемычка в горячем диске не образуется.

Если нет балджа и шкала гало $a\gee L$, то формирование глобального бара проходит качественно иным образом. Структуры типа ``двойного бара'' не образуются. Как мы видели в § 3.7, характерной особенностью развития глобальной бар-моды в первоначально очень холодном и тонком осесимметричном изолированном диске является возможность смещения центра бара относительно кинематического центра и центра тяжести дисковой компоненты. И в этом случае указанный фактор не позволяет сформироваться орбитам, перпендикулярным большой оси бара.

Таким образом, наиболее благоприятные условия для возникновения двойного бара имеются при наличии массивного балджа. Однако с уменьшением шкалы балджа важным оказывается механизм разрушения бар-моды, связанный с рассеянием частиц при пролете вблизи концентрированного ядра балджа (см. § 3.6). Рассеяние частиц наиболее эффективно для частиц, образующих внутренний бар, в результате его время жизни сокращается с уменьшением шкалы .

При учете приливных сил, связанных с движением спутника массы $M_{sput}$ по круговой орбите на радиусе $r=8L$ в плоскости диска, время жизни внутренней перемычки сокращается с увеличением массы $M_{sput}$. Это влияние является не прямым, а опосредованным — через формирование асимметричных возмущений в диске и внешнем баре.

Таким образом, сложные траектории частиц, обеспечивающие существование двойного бара, по-видимому, крайне неустойчивы по отношению к различного рода возмущениям, которые, помимо бар-моды, возникают на начальных стадиях (первые несколько оборотов вращения по внешнему краю диска). К ним относятся: транзиентные спиральные волны в плоскости диска, изгибы бара, изгибные неустойчивости диска. Аналогичное действие оказывает наличие внешнего несимметричного потенциала, связанного, например, с приливным воздействием. Расчеты в рамках звездно-газовых моделей с учетом небольшой доли газа ( $M_{gas}/M_{d}=0,\!15$) приводят к изменению характера развития гравитационной неустойчивости в центральной области -- стадия формирования внутреннего бара в экспериментах не наблюдается. Впрочем, этот вопрос требует дополнительных исследований.

=0.95

В построенных моделях структуры типа двойных баров являются временными образованиями на определенной стадии формирования бара. Этот вывод согласуется с небольшим временем жизни внутреннего бара и в работе [422]. В заключение отметим критический анализ А.В.Моисеева [117] кинематических данных наблюдений для галактик, в которых по фотометрическим данным обнаружены двойные бары. Показано, что в таких объектах внутренний бар не влияет на околоядерную кинематику газа и звезд. Тем самым, второй бар не является динамически выделенной галактической структурой. В то время как даже на короткой фазе ``двойного бара'' в построенных моделях кинематика в области внутренней структуры повторяет основные особенности кинематики внешнего бара.

3.9 Релаксационные пpоцессы в звездном диске

Обсуждению причин, которые могли бы объяснить наблюдаемую корреляцию между возрастом, дисперсией скоростей звезд и их шкалой высот, посвящено множество работ (см., например, монографию Марочника и Сучкова [107] и ссылки там; § 1.1). В данном разделе обсудим результаты только некоторых численных экспериментов, которые могли бы приблизить нас к пониманию природы связи между кинематическими параметрами и их эволюцией.

Наблюдения свидетельствуют об эволюции функции распределения скоростей звезд. В то же время звездно-звездные сближения в этом смысле заведомо неэффективны. Изменение скорости звезды в результате рассеяния пропорционально величине рассеивающей массы. Поэтому гигантские молекулярные облака (ГМО) могут служить важным фактором, влияющим на динамику звездного диска. Большие массы и размеры ГМО (см. § 1.2) позволяют эффективно рассеиваться на них звездам, что приводит к релаксационным процессам, увеличивая эффективную температуру звездного населения. Рассеяние на массивных неточечных объектах (например, ГМО) как возможный механизм изменения распределения скоростей звезд неоднократно обсуждался [87, 527, 571, 827, 906]. Его можно условно назвать механическим, в отличие от описанного в § 2.5, 3.5, где уже рассматривалась проблема анизотропии в распределении скоростей звезд и с точки зрения коллективных процессов -- устойчивости относительно изгибных мод.

3.9.1 Рассеяние на ГМО

Приведем некоторые результаты численного моделирования динамики звездного диска с учетом ГМО, следуя работам Вилумсена [879, 880]. Рассматривалась следующая модель. Распределение плотности звездного населения диска выбиралось в виде (ср. с (2.43))

$$\rho(r,z) = {M_d \o 2\,\pi\,L^2_\s z_e}\exp\left\{-{r \o L... ...t\}\,{\rm sech}^2\left\{-{z \o 2\,z_e}\right\}, %\eqno(3.4.1)$$ (3.48)

а в гало (3.3) при $k=1$. Распределению плотности вещества в ГМО

$$\rho_G(r) = {3\,M_G \o 4\,\pi\,r^3_G}\left[1 + {r^2 \o r^2_G} \right]^{-5/2} %\eqno(3.4.3)$$ (3.49)

соответствует потенциал

$$\Phi_G(r) = -{G\,M_G \o (r^2 + r^2_G)^{1/2}}. %\eqno(3.4.4)$$ (3.50)

Взаимодействие между звездами и ГМО учитывалось, только если расстояние между ними не превышало $r_{sG} = 2$ кпк. ГМО в начальный момент образовывали экспоненциальный диск с $L_G < L_\s$. Значения параметров выбирались в приложении к Галактике: $M_d = 0,\!5 \cdot 10^{11}$ М$_\odot$, $L_\s = 3,\!5$ кпк, $z_e = 0,\!325$ кпк, $M_h(r \le 30\,$кпк$) = 4M_d$, $a = 0,\!1$ кпк, общая масса ГМО -- $4 \cdot 10^9$ М$_\odot$. В расчетах варьировались начальные значения дисперсий и параметры ГМО. Число звезд $N_s$ и ГМО $N_G$ не превышало 4000 для каждой из подсистем, так что $0,\!1 \le N_G/N_s \le 1$.

На рис. 3.65 показана динамика трех компонент дисперсии скоростей звезд. В конце моделирования получается следующее отношение этих компонент для произвольной радиальной координаты:

$$c_r/c_\varphi/c_z = (1/0,\!72/0,\!60) \pm 0,\!04,$$ (3.51)

Представляет интерес сравнение данных Вилумсена с результатами Ласея [571], который получил следующее уравнение, описывающее эволюцию величины дисперсии ( $c^2 = c^2_r + c^2_\varphi + c^2_z$) вследствие столкновений с ГМО:

$${dc^2 \o dt} = {D \o c^2}, %\eqno(3.4.6)$$ (3.52)

где $D = 2\,G^2 n_G M^2_G\ln(\Lambda)\omega_z f(2\Omega /\varkappa)$, $n_G$ -- поверхностная концентрация ГМО; $f$ -- известная функция. Так как $2\Omega /\varkappa \simeq 1,\!4$, то, следуя Ласею, $f(1,\!4) = 0,\!47$; $\ln(\Lambda) = \ln(r_{sG}/r_G)$ и для условий экспериментов Вилумсена $\ln(\Lambda) = \ln(2\,{\rm кпк}/50\,{\rm пс}) = 3,\!7$. Запишем решение (3.52):

$$c(t) = \left(c^4_0 + 2\,D\,t\right)^{1/4},\qquad c_0 = c(t = 0).$$ (3.53)

Для полной экспериментальной дисперсии скоростей (см. рис. 3.7) и теоретической зависимости (3.53) в случае можно записать

$$\lg(c) = \lg(k) + n\,\lg(t);\qquad n \simeq 0,\!25.$$ (3.54)

В среднем различие между $k_{exp}$ и составляет 50 % [880].

Figure: Аппроксимация временной зависимости компонент ( $c_r, c_\varphi , c_z$) дисперсии скоростей по результатам численного моделирования Вилумсена [880]

=0.6

В связи с наблюдаемой зависимостью толщины звездного диска от возраста звезд упомянем также о возрастании со временем в экспериментах Вилумсена величины $\Delta_*$:

$$\lg\{\Delta_*(3\cdot 10^8\,\textrm{лет} \,\lee\, t \,\lee\,... ...rm{лет})\} = 0,\!91 + 0,\!36\,\lg\{t/10^6\,\textrm{лет}\}\,.$$

В моделях Ясумоту и Фудзимото [906] варьировались в широких пределах параметры, описывающие подсистему ГМО, помимо которых в рассмотрение включались спиральные волны плотности. В начале экспериментов звездные диски задавались холодными и на первом этапе наблюдался резкий рост дисперсии скоростей, затем, начиная с $t \simeq 10^9$ лет, было получено $c \propto t^n$ с $n = 0,\!20$. К моменту времени $t = 10^{10}$ лет в разных моделях $c \simeq 31 \div 47$ км/с. Для $M_G = 10^6 M_\odot$ и спиральной волны с углом закрутки $i = 10^\circ$ дисперсия достигала максимального значения ($\!47$ км/с). Получено, что характер пространственного распределения ГМО слабо влияет на темп роста дисперсии скоростей звезд ^3.20.

Следует сказать о том, что еще в 1961 г. Кузминым [87] были получены весьма близкие результаты. В рамках предположения, что гравитационное взаимодействие звезд с облаками диффузной материи должно приводить к росту как радиальной, так и вертикальной компонент дисперсии скоростей звезд, в равновесном пределе ( $c_z/c_r \rightarrow$ const) была получена следующая величина анизотропии:

$$\alpha_b = (1 + 4\,\Omega^2/\varkappa^2)^{1/2}.$$ (3.55)

Нетрудно видеть, что в невращающихся слоях и в твердотельно вращающихся дисках $(c_r/c_z)_b = \alpha^{-1}_b = 1/\sqrt{2} \simeq 0,\!71$, а в дифференциально вращающемся, как в окрестности Солнца ( $\Omega \propto r^{-1}$), диске должно быть $(c_z/c_r)_b \simeq 0,\!58$.

Итак, если эволюция функции распределения скоростей звезд определяется процессом рассеяния звезд на массивных облаках газа, то для подсистемы наиболее старых звезд диска $c_z / c_r \simeq 0,\!6$. Следует, однако, помнить, что рассмотренные выше модели достаточно грубо учитывают реальное распределение в пространстве рассеивающих объектов и их динамику на временах, сравнимых со временем жизни Галактики. В то же время надежные наблюдаемые значения величины $c_z/c_r$ относятся только к достаточно малой окрестности Солнца.

Однако, необходимо помнить, что ГМО являются тонкими структурами. Их толщина $h_{GMO}$ существенно меньше толщины старого звездного диска. В результате разогрев молодых звезд на ГМО оказывается эффективным только на начальной стадии. По мере увеличения вертикальной компоненты скорости звезды начинают проводить основное время в области $\vert z\vert\gg h_{GMO}\!$, и темп разогрева сильно уменьшается. Таким образом, трехмерные модели рассеяния звезд на ГМО не объясняют данные наблюдений, и, по-видимому, только совокупное действие различных механизмов может обеспечить высокий темп релаксационных процессов.

3.9.2 Экспоненциальный профиль яркости звездных дисков

Для радиального профиля яркости звездной компоненты $S$-галактик характерен за редким исключением экспоненциальный закон (1.1.1). Считается, что распределение поверхностной плотности $\sigma_\ast(r)$ имеет аналогичный вид. Универсальность радиальной зависимости $\sigma(r)_\ast\propto~ \exp(-r/L)$ требует объяснения. Наиболее разработанной является теория, основанная на учете вязкости в газовом диске и эффектов звездообразования [185, 344, 394, 584].

Воспользуемся уравнениями вязкой нестационарной аккреции (п. 4.1.1). В дополнение необходимо учесть: звездообразование, внешнюю аккрецию на диск, нестационарность кривой вращения газа. Тогда уравнение на поверхностную плотность газа $\sigma_g$ принимает вид:

$$\frac{\Vert\sigma_g}{\Vert t} = - \frac{\Vert}{r\,\Vert r}... ...nu \sigma_g r^3 \frac{\Vert\Omega}{\Vert r} \right] \right) +$$

$$+~\frac{\Vert}{r\,\Vert r} \left( \frac{\dot{m}_{e}\,r}{\... ... \Omega r^2/\Vert r} \frac{\Vert\Omega}{\Vert t} \right)\,,$$ (3.56)

где $\dot{m}_{e}$ - темп притока газа на единицу площади диска в результате аккреции, ${\cal L}_e$ определяет угловой момент аккрецирующего газа, $\psi$ - расход газа на образование звезд в расчете на единицу площади, и можно считать $\psi={\sigma_g}/{t_s}$ ($t_s$ - характерное время звездообразования). Первое слагаемое справа в (3.56) обусловлено действием вязкости $\nu$, второе - учитывает обмен моментом между веществом диска и аккрецирующим газом, последний член связан с изменением гравитационного потенциала из-за перераспределения вещества в диске. Баланс центробежной и гравитационной сил должен учитывать уравнение Пуассона. Звезды образуются из газа:

$$\frac{\Vert\sigma_\ast}{\Vert t} = \frac{\sigma_g}{t_s}.$$ (3.57)

В такой модели имеется два основных характерных времени: $t_\nu = ~r^2/\nu$ - вязкое время и $t_s$. Соотношение между $t_\nu$ и $t_s$ оказывается самым важным моментом теории эволюции галактического диска. Если $t_\nu \sim t_s$, то устанавливается экспоненциальное распределение звезд в диске [584]. Причем, этот результат слабо зависит от вида кривой вращения, выбора закона вязкости $\nu(\sigma_g,r)$ и внешней аккреции. Это может служить объяснением универсальности экспоненциального распределения $\sigma_\ast(r)$ у звездных дисков галактик различных типов.

3.10 Пpиливные эффекты

Весьма популярным является моделирование двойных галактик. Обычно распределение массы возмущающего спутника берут фиксированным, например, точечным. Тип орбиты спутника определяется постановкой задачи. Одними из первых провели численное моделирование такого рода А.Тоомре и Дж. Тоомре [854]. Целью таких экспериментов является изучение структур, вызываемых приливным взаимодействием [332, 440, 466]; процессов переноса и потери вещества [883]. В рамках численного эксперимента изучается и динамическое трение в близких парах [863]. В работе [840] рассматривались двухкомпонентные модели, включающие ``холодную'' (газовую) и ``горячую'' (звездную) подсистемы. Изучалось образование спиральных волн, вызванное пролетающим по параболической орбите в плоскости диска точечным спутником. Барнс и Хернквист сообщают [274] о моделировании динамики газа при слиянии двух галактик. Об интересной возможности образования газовых колец вокруг галактик в результате столкновения эллиптической и дисковой галактик сообщается в [437]. Следует также отметить возможность генерации бара пролетающим спутником.

В последние годы широкое распространение получает численное моделирование конкретных взаимодействующих галактик. Производится подгонка параметров галактик (массы, включая гало и газ; их орбиты; ориентации системы по отношению к лучу зрения; момента времени наблюдения и т. п.) для получения наилучшего согласия с наблюдаемыми данными; прежде всего речь идет о кривой вращения и спиральном узоре. Например, весьма полной получается картина у Бирда и Кларика [332] (пара AM 2208-251), Ховарда и Бирда [466] для галактик М51 - NGC 5195. В последнем случае учитывается также газовая подсистема, и авторы построенной модели даже предсказывают слияние галактик в будущем.

Актуальным является определение закона движения карликовых галактик вокруг гигантских галактик, например, спутника нашей Галактики -- Большого Магелланова Облака. Приближенное уравнение движения частицы массой $m_i$ внутри массивного гало массой $M_h$ с учетом динамического трения имеет вид [464, 519]:

$$\frac{d\vec{v}}{dt} = - \vec{\nabla}\Phi(r) -16 \pi^2 G^2 ... ...{v_{\max}} f(v)\,d\vec{v}}{\vert\vec{v}\vert^3}\,\vec{v} \,,$$ (3.58)

где $\Phi$ -- потенциал, $\Oo \ln\Lambda = \ln\left( R_h/\varepsilon_s V_s^2 \right)$ -- кулоновский логарифм, $f(\vec{v})$ - функция распределения, $R_h$ -- шкала гало, $\varepsilon_s$ -- характерный радиус обрезания. Моделирование диска методом $N\!$-тел с учетом эволюции темного гало приводит к большому времени жизни таких систем, в частности, БМО за счет динамического трения поглотится Галактикой только через $1,4\cdot 10^{10}$ лет [464].

В последние годы появляется возможность строить численные модели взаимодействующих многокомпонентных систем. При прохождении карликовой галактики сквозь дисковую галактику моделирование наглядно демонстрирует возможность формирования бароподобных, кольце- и спицеобразных структур, различных асимметричных образований в звездной и газовой компонентах [290 ]. Тесные взаимодействия, приводящие к падению компактного спутника, в некоторых случаях способны существенно ослабить центральный бар и даже разрушить его [291].

Общепринятой является точка зрения на природу галактик типа ``тележного колеса'' (Cartwheel), возникновение которых связывают с падением спутника на галактику, богатую газом [494]. В эволюционных моделях, включающих звездообразование, происходит формирование радиально вытянутых возмущений (спиц) и внешнего кольца в диске [626]. В результате появляются характерные градиенты параметров звездной и газовой подсистем [881].

<< 2. Динамика звездного диска 4. Аккpеционные диски >>