Рассмотрим подробнее первый сомножитель в подынтегральном
выражении основных формул (1.7)-(1.9):
функцию ![]() для звезд
разных спектральных классов и классов светимости. В этом нам
помогут спектрофотометрические данные о распределении энергии.
Для ``нормальных'', т.е. освобожденных от влияния межзвездного
покраснения, распределений эти данные в достаточном для нас
объеме содержатся в уже упомянутой статье Свидерскене. Страйжис
и Свидерскене начали эту работу еще в 60-х годах. По всему
доступному библиографическому материалу были собраны
спектрофотометрические данные о распределениях энергии в
спектрах различных звезд. Все сведения были внимательно
просмотрены и представлены для набора 50-ангстремных интервалов.
В необходимых случаях в распределениях энергии были исправлены
искажения, вносимые небольшим межзвездным поглощением, хотя
авторы и старались отбирать звезды, для которых поглощение
пренебрежимо мало. Потом эти данные были усреднены для всех
рассмотренных звезд данного типа и представлены в нескольких
каталогах. Наиболее полный вариант такого каталога вышел в 1988г.
Рассмотрим кривые для некоторых из этих распределений
энергии, обращая внимание на различия между ними по существу.
для звезд
разных спектральных классов и классов светимости. В этом нам
помогут спектрофотометрические данные о распределении энергии.
Для ``нормальных'', т.е. освобожденных от влияния межзвездного
покраснения, распределений эти данные в достаточном для нас
объеме содержатся в уже упомянутой статье Свидерскене. Страйжис
и Свидерскене начали эту работу еще в 60-х годах. По всему
доступному библиографическому материалу были собраны
спектрофотометрические данные о распределениях энергии в
спектрах различных звезд. Все сведения были внимательно
просмотрены и представлены для набора 50-ангстремных интервалов.
В необходимых случаях в распределениях энергии были исправлены
искажения, вносимые небольшим межзвездным поглощением, хотя
авторы и старались отбирать звезды, для которых поглощение
пренебрежимо мало. Потом эти данные были усреднены для всех
рассмотренных звезд данного типа и представлены в нескольких
каталогах. Наиболее полный вариант такого каталога вышел в 1988г.
Рассмотрим кривые для некоторых из этих распределений
энергии, обращая внимание на различия между ними по существу.
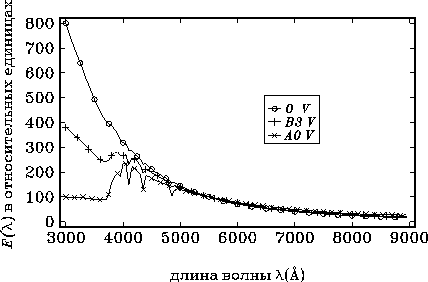
Начнем со спектра непокрасненной звезды спектрального класса O (рис.2.2).
 |
Подобные простые и гладкие спектры очень удобно
использовать для подстановки в основные формулы (1.7), (1.8),
когда нужно определять параметры, не связанные с самим
распределением энергии, например, параметры атмосферной
экстинкции. Чем проще вид спектра ![]() , тем менее вероятно, что
в нашу спектральную полосу будут входить участки с большими
градиентами.
, тем менее вероятно, что
в нашу спектральную полосу будут входить участки с большими
градиентами.
Рассмотрим теперь спектр B3V (см. рис.2.2). Перепад
удельных освещенностей от
![]() до
до
![]() в два
раза меньше, чем у спектра O. Кроме того, гладкость этого спектра
уже нарушена. Появился бальмеровский скачок при
в два
раза меньше, чем у спектра O. Кроме того, гладкость этого спектра
уже нарушена. Появился бальмеровский скачок при
![]() . Если
спектр O-звезды был очень похож на распределение энергии в спектре
абсолютно черного тела, то бальмеровский скачок и появившиеся
бальмеровские и другие спектральные линии явно искажают эту картину. Из
формул излучения абсолютно черного тела следует линейная зависимость
между различными (чернотельными) показателями цвета. Детали в спектрах
реальных звезд, появляющиеся вследствие спектрального перераспределения
энергии в звездных атмосферах, делают взаимные зависимости этих
показателей цвета нелинейными и немонотонными. Применяемые обратные
функции становятся при этом неоднозначными, что сильно затрудняет все
редукции, связанные с необходимостью приводить результаты наблюдений в
инструментальных фотометрических полосах в систему со стандартными
полосами.
. Если
спектр O-звезды был очень похож на распределение энергии в спектре
абсолютно черного тела, то бальмеровский скачок и появившиеся
бальмеровские и другие спектральные линии явно искажают эту картину. Из
формул излучения абсолютно черного тела следует линейная зависимость
между различными (чернотельными) показателями цвета. Детали в спектрах
реальных звезд, появляющиеся вследствие спектрального перераспределения
энергии в звездных атмосферах, делают взаимные зависимости этих
показателей цвета нелинейными и немонотонными. Применяемые обратные
функции становятся при этом неоднозначными, что сильно затрудняет все
редукции, связанные с необходимостью приводить результаты наблюдений в
инструментальных фотометрических полосах в систему со стандартными
полосами.
Прокомментируем теперь общий вид распределения энергии в спектре
звезды A0V (см. рис.2.2, 2.4, 2.3).
Первое, что бросается в глаза, это громадная амплитуда бальмеровского
скачка и великолепно развитые бальмеровские линии. Это хорошо видно
даже с низким спектральным разрешением
![]() . Но, в общем, спектр еще
достаточно ровный, и использовать его для исследования атмосферных
функций вполне приемлемо. Общий перепад удельных освещенностей в 2 раза
меньше, чем у звезд B3V, и максимум излучения уже попадает в
спектральный интервал
. Но, в общем, спектр еще
достаточно ровный, и использовать его для исследования атмосферных
функций вполне приемлемо. Общий перепад удельных освещенностей в 2 раза
меньше, чем у звезд B3V, и максимум излучения уже попадает в
спектральный интервал
![]() и находится около
и находится около
![]() .
.
Ранее говорилось, что для первичного фотометрического стандарта
![]() Lyr звезды A0V у разных авторов расходятся данные в ближней
ультрафиолетовой области. Речь идет о различных величинах наклона
спектра в бальмеровском континууме, вызванных систематическими
ошибками. С этими ошибками спектрофотометристам еще придется
разбираться. Но нельзя думать, что различия между распределениями
энергии в спектрах звезд одного и того же спектрального типа вызваны
только систематическими ошибками. Между ними существуют и реальные
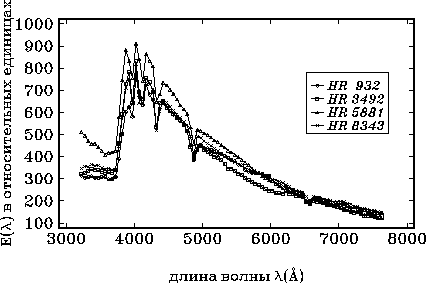
физические различия. На рис.2.3 показаны несколько спектров,
взятых из Московского спектрофотометрического каталога, для звезд,
принадлежащих к типу A0V. Все эти распределения нормированы так, чтобы
соответствовать звезде нулевой визуальной величины.
Lyr звезды A0V у разных авторов расходятся данные в ближней
ультрафиолетовой области. Речь идет о различных величинах наклона
спектра в бальмеровском континууме, вызванных систематическими
ошибками. С этими ошибками спектрофотометристам еще придется
разбираться. Но нельзя думать, что различия между распределениями
энергии в спектрах звезд одного и того же спектрального типа вызваны
только систематическими ошибками. Между ними существуют и реальные
физические различия. На рис.2.3 показаны несколько спектров,
взятых из Московского спектрофотометрического каталога, для звезд,
принадлежащих к типу A0V. Все эти распределения нормированы так, чтобы
соответствовать звезде нулевой визуальной величины.
По мере продвижения к более поздним спектрам вид распределения энергии начинает усложняться. Сделаем несколько комментариев к спектру звезд типа G2V (см. рис.2.4).
 |
Глядя на спектр типа G2V, вспомним процедуру определения
спектрального класса. Для проведения классификации берутся значения
отношения интенсивностей (эквивалентных ширин) избранных линий
поглощения и эти значения сравниваются со стандартными калибровочными
величинами. Например, как указывается в Пулковском курсе, для
сравнительно ранних подклассов спектрального типа G при определении
спектрального класса рассматривают отношения
(FeI![]() )/H
)/H![]() и (CaI
и (CaI![]() )/H
)/H![]() , а
при определении класса светимости --
(SrII
, а
при определении класса светимости --
(SrII![]() )/(CaI
)/(CaI![]() ) и
(SrI
) и
(SrI![]() )/(FeI
)/(FeI![]() ).
).
Когда мы говорим о спектрофотометрии, то понимаем под этим процесс
получения функции распределения энергии в спектре при достаточно низком
спектральном разрешении, когда нужно лишь в общих чертах
охарактеризовать данную функцию. При этом индикаторами спектрального
класса становятся отношения интегралов
![]() и
и
![]() ,
т.е. внеатмосферные показатели цвета для полос
,
т.е. внеатмосферные показатели цвета для полос ![]() и
и ![]() . В отличие
от отношений интенсивностей спектральных линий, эти показатели цвета
могут быть, помимо всего прочего, искажены межзвездным поглощением.
Понятно, что спектральные классы, полученные по линиям, и спектральные
классы, полученные из показателей цвета, по многим причинам могут не
совпадать и вообще представляют собой разные(!) физические
параметры. Они, конечно, сильно коррелируют, так как в основном
обусловлены температурой на поверхности звезды, но кроме температуры на
определение спектральных классов влияет целый ряд других факторов.
Прежде всего, это вариации химического состава звездных атмосфер и
изменение поверхностного ускорения силы тяжести при переходе от звезд
главной последовательности к гигантам и сверхгигантам. Определив
спектральный класс по отношению интенсивностей нескольких пар
спектральных линий, мы в общем случае еще не можем достаточно точно
сопоставить этому спектральному классу то или иное распределение
энергии в спектре. На примере нескольких звезд A0 мы уже видели, что
существуют звезды с одинаковой спектральной классификацией по линиям,
но с различающимися распределениями энергии, т.е. с разными
показателями цвета. В противоположность этому можно указать на
существование звезд с почти одинаковым распределением энергии в
визуальной области спектра (т.е. с одинаковыми показателями цвета),
классифицирующиеся по линиям как звезды разных спектральных подклассов.
В итоге будущей большой фотометрической и спектрофотометрической работы
должна возникнуть ``спектрофотометрическая'' классификация звездных
спектров.
. В отличие
от отношений интенсивностей спектральных линий, эти показатели цвета
могут быть, помимо всего прочего, искажены межзвездным поглощением.
Понятно, что спектральные классы, полученные по линиям, и спектральные
классы, полученные из показателей цвета, по многим причинам могут не
совпадать и вообще представляют собой разные(!) физические
параметры. Они, конечно, сильно коррелируют, так как в основном
обусловлены температурой на поверхности звезды, но кроме температуры на
определение спектральных классов влияет целый ряд других факторов.
Прежде всего, это вариации химического состава звездных атмосфер и
изменение поверхностного ускорения силы тяжести при переходе от звезд
главной последовательности к гигантам и сверхгигантам. Определив
спектральный класс по отношению интенсивностей нескольких пар
спектральных линий, мы в общем случае еще не можем достаточно точно
сопоставить этому спектральному классу то или иное распределение
энергии в спектре. На примере нескольких звезд A0 мы уже видели, что
существуют звезды с одинаковой спектральной классификацией по линиям,
но с различающимися распределениями энергии, т.е. с разными
показателями цвета. В противоположность этому можно указать на
существование звезд с почти одинаковым распределением энергии в
визуальной области спектра (т.е. с одинаковыми показателями цвета),
классифицирующиеся по линиям как звезды разных спектральных подклассов.
В итоге будущей большой фотометрической и спектрофотометрической работы
должна возникнуть ``спектрофотометрическая'' классификация звездных
спектров.
Остановимся теперь на распределении энергии в спектре карлика K5
(см. рис.2.4). В ультрафиолетовой части (
![]() ) такая звезда излучает крайне мало. С увеличением длины волны
спектр круто идет вверх и максимум кривой энергии приходится примерно
на
) такая звезда излучает крайне мало. С увеличением длины волны
спектр круто идет вверх и максимум кривой энергии приходится примерно
на
![]() . Этот спектр также нельзя назвать гладким.
Бальмеровские линии не заметны, но есть мощные полосы поглощения,
делающие вид спектра ``волнистым''. При сравнительно невысокой
температуре фотосферы звезды эти полосы создаются не атомами, а
молекулами. Среди них хорошо известны полосы окиси титана.
. Этот спектр также нельзя назвать гладким.
Бальмеровские линии не заметны, но есть мощные полосы поглощения,
делающие вид спектра ``волнистым''. При сравнительно невысокой
температуре фотосферы звезды эти полосы создаются не атомами, а
молекулами. Среди них хорошо известны полосы окиси титана.
В каталоге Свидерскене распределения энергии в спектрах
представлены с нормировкой на излучение с длиной волны
![]() . Это соответствует случаю рассмотрения звезд разных
спектральных классов, но с одинаковой монохроматической звездной
величиной у
. Это соответствует случаю рассмотрения звезд разных
спектральных классов, но с одинаковой монохроматической звездной
величиной у
![]() . Если для таких распределений вычислить
звездные величины в фотометрической полосе
. Если для таких распределений вычислить
звездные величины в фотометрической полосе ![]() по формуле (1.9),
то эти величины, разумеется, будут разными для разных спектральных
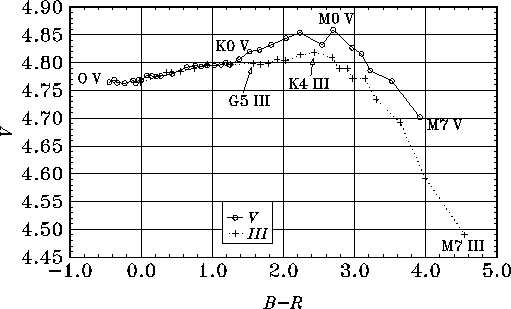
типов. Рассматриваемое явление называется эффектом ширины полосы. Его
иллюстрирует рис.2.5.
по формуле (1.9),
то эти величины, разумеется, будут разными для разных спектральных
типов. Рассматриваемое явление называется эффектом ширины полосы. Его
иллюстрирует рис.2.5.
 |
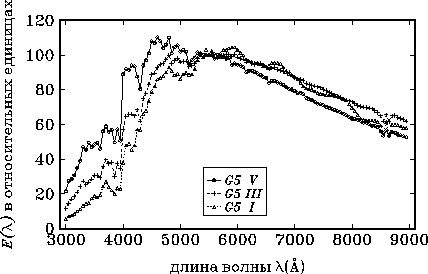
Пример различий в распределении энергии в спектре звезд одного спектрального класса, но разных классов светимости показан на рис.2.6, где представлены распределения для карлика, гиганта и сверхгиганта спектрального класса G5.
 |
Все сказанное имеет большое значение при выработке оптимальной
методики выноса звездных величин за атмосферу и вычисления поправок
для перевода величин из одной фотометрической полосы в другую.
Конечно, все зависит от заданной степени точности. Если вас устраивает
среднеквадратическая ошибка редукций 3-4%,
то большинством указанных различий можно пренебречь, но это уже нельзя
назвать прецизионной фотометрией. Например, Джонсон редуцировал
ультрафиолетовые показатели цвета за атмосферу и на стандартную систему
UBV без учета зависимостей их от спектрального класса. В частности,
поэтому его различные ряды наблюдений одних и тех же ярких звезд,
выполненные с однотипной аппаратурой, но в разные годы и в разных
обсерваториях, сходятся друг с другом со среднеквадратичным отклонением
![]() .
.
Еще раз подчеркнем, что аппаратура для электрофотометрических измерений принципиально способна измерять световые потоки с точностью в доли процента. Следовательно, методика наблюдений и обработки в фотоэлектрической фотометрии должна позволять хотя бы приблизиться к этому уровню точности.