Термин аккреционный диск (АД) обычно употребляется для обозначения газового диска вокруг массивного (по сравнению с диском) компактного объекта. К последним относятся белые карлики, нейтронные звезды, черные дыры. Определяющей чертой АД является переход гравитационной энергии при аккреции (падении) вещества в тепло с последующим излучением. Весьма часто понятием ``аккреционный диск'' пользуются в более широком смысле, имея в виду газовый диск, для которого существен процесс падения вещества на аккумулирующий центр, например, когда речь идет о протозвездных, протопланетных, галактических дисках.
Таким образом, с точки зрения физических процессов любые
результаты, относящиеся к газовым дискам, в полной мере относятся
к АД. Поэтому различие между главами 4 и 5 весьма условно и
связано в основном с видом внешнего потенциала. Для дисков,
вращающихся вокруг компактных объектов массой ![]() , он является
ньютоновым для точечного тела (
, он является
ньютоновым для точечного тела (
![]() ), и
самогравитация газа несущественна, за исключением, пожалуй, дисков
вокруг сверхмассивных черных дыр. В случае галактических газовых
дисков внешний потенциал определяется распределением звездного
вещества (см. (2.44)), и самогравитация часто
оказывается весьма важным фактором.
), и
самогравитация газа несущественна, за исключением, пожалуй, дисков
вокруг сверхмассивных черных дыр. В случае галактических газовых
дисков внешний потенциал определяется распределением звездного
вещества (см. (2.44)), и самогравитация часто
оказывается весьма важным фактором.
Одной из ключевых проблем физики
аккреционных дисков является вопрос о механизмах отвода углового
момента, обеспечивающих падение вещества на гравитирующий центр.
Достигнутый прогресс в немалой степени основан на
вязких моделях
аккреционных дисков (АД) [
252,
253,
280,
304,
689,
790,
814, 842
и др.].
По-видимому, первым рассмотрел механизм переноса момента импульса
из-за действия вязкости еще C.F.![]() von Weizsacker в 1948 г.
[892].
Другой возможностью
является отвод углового момента посредством крупномасштабных
спиральных ударных волн, которые могут формироваться при
перетекании газа в тесных двойных системах (ТДС) с учетом
гравитационного влияния звезды-донора
[16,
302,
829,
830].
von Weizsacker в 1948 г.
[892].
Другой возможностью
является отвод углового момента посредством крупномасштабных
спиральных ударных волн, которые могут формироваться при
перетекании газа в тесных двойных системах (ТДС) с учетом
гравитационного влияния звезды-донора
[16,
302,
829,
830].
Вязкие модели АД, в основе которых лежит гипотеза о турбулентной
вязкости (![]() -модель Шакуры и Сюняева
[221,
790] и ее многочисленные
модификации), позволяют объяснить многие наблюдения в ТДС,
активных галактических ядрах (АГЯ), протозвездных дисках, однако
удовлетворительной нефеноменологической модели турбулентной
вязкости в настоящее время нет.
Вязкость может играть важную роль в газовых галактических дисках
[34,
184].
Следует отметить, что, несмотря на достижения последних лет
[271,
304,
653,
696,
845,
857],
активное изучение
турбулентности в аккрецирующих системах только
начинается и основные результаты еще впереди.
-модель Шакуры и Сюняева
[221,
790] и ее многочисленные
модификации), позволяют объяснить многие наблюдения в ТДС,
активных галактических ядрах (АГЯ), протозвездных дисках, однако
удовлетворительной нефеноменологической модели турбулентной
вязкости в настоящее время нет.
Вязкость может играть важную роль в газовых галактических дисках
[34,
184].
Следует отметить, что, несмотря на достижения последних лет
[271,
304,
653,
696,
845,
857],
активное изучение
турбулентности в аккрецирующих системах только
начинается и основные результаты еще впереди.
Имеется много работ, посвященных линейному анализу устойчивости вязких АД [36, 149, 205, 209, 230, 245, 270, 271, 303, 335, 538, 580, 617, 643, 791, 884, 885, 842 и др.]. Однако вопрос о последствиях развития неустойчивостей на существенно нелинейных стадиях только начинает рассматриваться в рамках численного гидродинамического моделирования [212, 233, 237, 272, 510, 647, 857].
Проблема конвекции в газовых дисках восходит к работам Вейцзеккера [892] и Сафронова [183]. Развитие ADAF-моделей (адвективно доминирующие аккреционные течения) для объяснения низкой светимости рентгеновских двойных и активных галактических ядер с черными дырами [231, 508, 659] привело к построению CDAF-моделей (конвективно-доминирующие аккреционные течения), в которых при слабой вязкости формируются течения с сильной турбулентностью из-за развития конвективной неустойчивости [272, 506, 663, 837]. Другим примером вертикальной конвекции в газовом диске является неустойчивость в радиационно-доминирующей области [237, 303]. При учете ионизации водорода получаются неустойчивые вертикальные распределения температуры, приводящие к конвективному переносу тепла [514, 624, 814].
Характерной чертой аккрецирующих систем является широкий спектр нестационарных проявлений (карликовые новые различных типов: SS Лебедя, SU Большой Медведицы, Z Жирафа; рентгеновские пульсары; рентгеновские барстеры I и II типов; квазипериодические осцилляции рентгеновских источников; переменность излучения у кандидатов в черные дыры: Cyg X-1, GX 339-4, Cir X-1). Для объяснения некоторых переменностей излучения важным представляется изучение нестационарных течений, которые обусловлены развитием гидродинамических (МГД) неустойчивостей.
Наличие магнитного поля существенно усложняет гидродинамические течения в гравитационном поле компактного объекта, где разнообразие неустойчивостей плазмы, по-видимому, не меньше, чем для термоядерной плазмы [112]. Магнитные поля играют важную роль в динамике ряда аккреционно-струйных систем вблизи компактных звезд. В частности, влияют на структуру струй, характер и темп аккреции [17, 304, 653, 696].
Активное изучение турбулентности в аккрецирующих системах должно привести, в частности, к построению нефеноменологических моделей турбулентной вязкости [15, 149, 304, 354, 570]. Существенная доля газа в галактиках, протопланетных и протозвездных дисках и подавляющая его часть в аккрецирующих системах представляет собой полностью или частично ионизованную плазму. В плазме может существовать большое число неустойчивых мод, развитие которых эффективно турбулизует вещество. Без преувеличения можно сказать, что турбулентность является естественным состоянием для плазмы. Причем, одновременно могут работать много механизмов, приводящих к турбулентности через нелинейную стадию неустойчивостей.
В первом параграфе рассмотрены модели осесимметричных аккреционных дисков, в основе которых лежит предположение о переносе углового момента по диску за счет вязкости. В § 4.2 представлены в некотором смысле альтернативные результаты, связанные с возможностью образования спиральных волн (в том числе ударных) в газовых дисках. В § 4.3 рассмотрены некоторые магнитогазодинамические неустойчивости, которые при определенных условиях могут играть важную роль в аккреционных дисках. Интерес к такого рода исследованиям связан с тем, что неустойчивости могут приводить к эффективной турбулизации вещества в АД, определять механизм проникновения плазмы на замагниченные компактные объекты, приводить к различного рода нестационарным процессам.
Сама идея механизма, приводящего к переносу углового момента в
осесимметричном диске и, следовательно, аккреции вещества,
достаточно проста. Она заключается в том, что в дифференциально
вращающейся среде происходит взаимодействие между соседними
слоями, связанное, например, с существованием магнитного поля,
турбулентности, молекулярной или радиационной вязкости и
т. п.4.1. При типичных условиях молекулярная вязкость не
может обеспечить величину темпа аккреции, вытекающую из
наблюдений, а радиация сама является следствием аккреции.
Магнитное поле попадает в диск, например, вместе с веществом,
вытекающим из нормальной звезды. При определенных условиях
величина магнитного поля может достигать
![]() , что является достаточным для аккреции.
, что является достаточным для аккреции.
В основе рассмотренной ниже осесимметричной модели лежит, как и в
главе 4, предположение о том, что толщина диска ![]() везде мала
по сравнению с радиальной координатой
везде мала
по сравнению с радиальной координатой ![]() .
.
Запишем уравнения газодинамики с учетом диссипации для
осесимметричного диска вокруг центрального тела массой ![]() .
Закон сохранения массы запишем с учетом источника вещества
.
Закон сохранения массы запишем с учетом источника вещества
Турбулентную среду можно при описании крупномасштабного
движения рассматривать как жидкость, обладающую турбулентной
вязкостью ![]() , отличной от истинной (молекулярной)
кинематической вязкости [92].
Развитую турбулентность можно рассматривать как иерархию
турбулентных пульсаций, различающихся пространственными
масштабами. Если через
, отличной от истинной (молекулярной)
кинематической вязкости [92].
Развитую турбулентность можно рассматривать как иерархию
турбулентных пульсаций, различающихся пространственными
масштабами. Если через ![]() и
и ![]() обозначить соответственно
скорость и масштаб основного (наиболее крупномасштабного)
турбулентного движения, то по порядку величины можно записать
обозначить соответственно
скорость и масштаб основного (наиболее крупномасштабного)
турбулентного движения, то по порядку величины можно записать
В предположении об изотропной турбулентности естественно
предположить
![]() . Поскольку сверхзвуковые
турбулентные пульсации быстро диссипируют, то
. Поскольку сверхзвуковые
турбулентные пульсации быстро диссипируют, то
![]() .
В результате имеем
.
В результате имеем
В отсутствие сколько-нибудь законченной теории турбулентности
чрезвычайно важной стала работа Шакуры
[221], который, по меткому выражению,
``свел все наше незнание турбулентности к одному
безразмерному параметру ![]() '' [100]. Для
тензора вязких напряжений принимается
'' [100]. Для
тензора вязких напряжений принимается
где ![]() -- усредненное по
-- усредненное по ![]() -координате давление;
-координате давление;
![]() -- свободный параметр. Модели, в основе которых лежит
соотношение типа (4.6), принято называть
-- свободный параметр. Модели, в основе которых лежит
соотношение типа (4.6), принято называть
![]() -моделями или стандартными моделями АД.
-моделями или стандартными моделями АД.
В уравнении состояния вещества будем учитывать
газовое, радиационное и магнитное давление
Рассмотрим структуру диска в ![]() -направлении. Будем полагать, что
в
-направлении. Будем полагать, что
в ![]() -направлении вещество находится в гидростатическом
равновесии (см. (
-направлении вещество находится в гидростатическом
равновесии (см. (![]() ))
))
Обратимся к радиальной компоненте уравнения движения
(![]() )
)
Следует подчеркнуть приближенный характер соотношения
(4.14), что особенно важнo при изучении динамики
звуковых возмущений в плоскости диска. Диск не является строго
кеплеровским, в противном случае в нем не могли бы
распространяться крупномасштабные (![]() ) звуковые волны.
Отличие скорости вращения от кеплеровской обусловлено
практически только давлением, поскольку диссипативные члены в
(4.11) малы
) звуковые волны.
Отличие скорости вращения от кеплеровской обусловлено
практически только давлением, поскольку диссипативные члены в
(4.11) малы
![]() .
.
Используя (4.14), исключим из
(4.1) и (4.2) радиальную
скорость, в результате получим эволюционное уравнение для
поверхностной плотности
Рассмотрим уравнение баланса энергии для вещества диска в
следующем виде:
В качестве основных источников непрозрачности вещества в АД
обычно принимают [222]: рассеяние на
свободных электронах
Таким образом, задача определения эволюции АД в рамках
построенной модели сводится к совместному решению системы
уравнений (4.15)![]() (4.21
или 4.22), (4.7),
(4.10). В результате для определенного начального
состояния рассчитывается зависимость параметров диска (
(4.21
или 4.22), (4.7),
(4.10). В результате для определенного начального
состояния рассчитывается зависимость параметров диска (![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,...) от времени и радиальной
координаты. При таком подходе функции
,...) от времени и радиальной
координаты. При таком подходе функции ![]() ,
, ![]() ,
,
![]() должны задаваться из каких-то дополнительных
соображений. Процедура ввода в диск вещества и энергии описана в
[280,
281,
282]. Учету приливного
взаимодействия в рамках осесимметричных моделей посвящены работы
[592,
691,
719,
814].
должны задаваться из каких-то дополнительных
соображений. Процедура ввода в диск вещества и энергии описана в
[280,
281,
282]. Учету приливного
взаимодействия в рамках осесимметричных моделей посвящены работы
[592,
691,
719,
814].
Характерными временами дисковой аккреции являются:
динамическое время
![]() , время
установления гидростатического равновесия в
, время
установления гидростатического равновесия в ![]() -направлении
-направлении
![]() , тепловой временной масштаб
, тепловой временной масштаб
![]() и обусловленное вязкостью
и обусловленное вязкостью
![]() . Соотношения между этими
величинами зависят от радиальной координаты, но в целом можно
считать
. Соотношения между этими
величинами зависят от радиальной координаты, но в целом можно
считать
Остановимся несколько подробнее на учете
приливного взаимодействия. Под действием вязких сил
диск в отсутствие приливного взаимодействия
неограниченно ``расползается'' в радиальном
направлении. Радиус диска стремится к бесконечности.
Угловой момент благодаря трению отводится из внутренних
областей диска во внешние и при наличии
объекта-донора диск может простираться только до
радиуса, на котором приливное взаимодействие
способно отвести весь угловой момент из диска. В
стационарном случае общий угловой момент вещества есть
величина постоянная, следовательно, должен выполняться
баланс
Большинство работ, в которых учитывалось в (4.15)
приливное взаимодействие, основывается на результатах Папалоизу и
Прингла [691].
Удобно величину ![]() представить в виде
представить в виде
При изучении стационарных моделей достаточно во всех
эволюционных уравнениях п. 4.1.1 положить
. В рамках некоторых предположений о
виде законов непрозрачности, вязкости и переноса энергии удается
получить аналитические зависимости параметров АД от радиальной
координаты. Обычно, следуя Шакуре и Сюняеву
[790], диск разбивается на
несколько областей, в которых преимущественную роль играют
определенные процессы переноса излучения (![]() или )
и давление ( или
или )
и давление ( или ![]() ), приливное взаимодействие не
учитывается, пpинимается
), приливное взаимодействие не
учитывается, пpинимается
![]() .
.
1. В самой внутренней радиационно доминирующей (
![]() ) зоне диска ``a'' с учетом выполнения
) зоне диска ``a'' с учетом выполнения
![]() имеем:
имеем:
2. Для области ``b'', где
![]() и
и
![]() , можно записать:
, можно записать:
3. Во внешней области диска ``c'' (
![]() ,
,
![]() ):
):
Отметим, что в зависимости от конкретных значений параметров системы та или иная область может отсутствовать в диске.
В настоящее время имеется большое количество работ, посвященных определению радиальной структуры АД при тех или иных условиях. Описание некоторых моделей можно найти в работах [144, 209, 304].
Наряду с лучистым переносом энергия из внутренних слоев диска
может выноситься наружу конвективным движением (см.
(4.18)). Однако радиационный перенос всегда
имеет место при высокой температуре, а конвекция может и не
возникать. Роль и условия возникновения конвекции в приложении
к внутреннему строению звезд подробно исследованы (см., например,
[21]). Имеется ряд факторов, не
позволяющих формально перенести результаты теории звезд на
аккреционные диски. Прежде всего отличается зависимость силы
тяжести от координаты и имеется сильная вязкость. На важность
учета конвекции в газовых дисках было указано Пачинским
[687]; Вила
[877,
878] рассматривал конвективные модели
холодных дисков в катаклизмических двойных и массивных горячих
дисках, а Лин и Папалоизу
[582] исследовали
протопланетный диск с конвекцией. Построению нестационарных
моделей, основанных на детальном расчете ![]() -структуры, посвящены
работы
[392,
616,
813,
814] и др. В приложении к галактическим
ядрам конвективную неустойчивость рассматривали Минешига и Осаки
[638].
-структуры, посвящены
работы
[392,
616,
813,
814] и др. В приложении к галактическим
ядрам конвективную неустойчивость рассматривали Минешига и Осаки
[638].
Для конвективного потока тепла можно записать
Мейер и Мейер-Хофмейстер [615]
обнаружили неустойчивое распределение температуры, обусловленное
ионизацией водорода. При ионизации водорода (
![]() К) непрозрачность
К) непрозрачность ![]() сильно меняется по
величине, так что радиационный механизм переноса энергии не может
уже обеспечить необходимый темп. Образуется резкий перепад
температуры между внутренними слоями, где в основном генерируется
тепло, и внешними, из которых происходит высвечивание. В
результате возникают условия для конвективного движения. При
детальном расчете переноса излучения, естественно, нельзя
пользоваться простыми соотношениями для непрозрачности типа
(4.21), (4.22), тем более,
что возможно нарушение приближения оптически толстого диска
[616,
814]. Обычно используют таблицы
непрозрачности (см., например,
[21]).
сильно меняется по
величине, так что радиационный механизм переноса энергии не может
уже обеспечить необходимый темп. Образуется резкий перепад
температуры между внутренними слоями, где в основном генерируется
тепло, и внешними, из которых происходит высвечивание. В
результате возникают условия для конвективного движения. При
детальном расчете переноса излучения, естественно, нельзя
пользоваться простыми соотношениями для непрозрачности типа
(4.21), (4.22), тем более,
что возможно нарушение приближения оптически толстого диска
[616,
814]. Обычно используют таблицы
непрозрачности (см., например,
[21]).
=0.57 |
Типичная зависимость эффективной температуры поверхности диска
![]() от величины поверхностной плотности
вещества показана на рис. 4.1. Каждая кривая
имеет характерную
от величины поверхностной плотности
вещества показана на рис. 4.1. Каждая кривая
имеет характерную ![]() -форму
-- состоит из трех участков: холодный
-форму
-- состоит из трех участков: холодный ![]() , горячий
, горячий ![]() и
переходный
и
переходный ![]() . Область
. Область ![]() соответствует неустойчивости, тогда
как горячие и холодные решения термически устойчивы. Поскольку
вещество при
соответствует неустойчивости, тогда
как горячие и холодные решения термически устойчивы. Поскольку
вещество при
![]() К практически полностью
ионизовано, горячий участок определяется достаточно уверенно.
Этого нельзя сказать об участке
К практически полностью
ионизовано, горячий участок определяется достаточно уверенно.
Этого нельзя сказать об участке ![]() . В области низких температур
закон непрозрачности известен хуже, холодный участок может быть
оптически тонким, именно поэтому ветвь
. В области низких температур
закон непрозрачности известен хуже, холодный участок может быть
оптически тонким, именно поэтому ветвь ![]() менее определена и
имеются отличия у разных авторов [876].
менее определена и
имеются отличия у разных авторов [876].
Характерной чертой карликовых новых (звезд типа U-Gem и дp.) является их нестационарное поведение (п. 1.5). В настоящее время предложено немало механизмов для объяснения феномена карликовых новых и в целом катаклизмических переменных [33]. Взрывной характер поведения многих систем обусловлен, по-видимому, нестационарным режимом дисковой аккреции. Весь вопрос заключается в определении местонахождения ``клапана'', который ``открывается'' на определенное время, что в конечном счете приводит к вспышке. Можно выделить три типа механизмов:
1. Причина нестационарности связана с нормальной
звездой. Вследствие нестабильности вытекания вещества из красного
карлика возникают квазипериодические колебания в накоплении
вещества диском и тем самым в светимости газового диска
[279]. Поскольку газ в АД поступает
определенными порциями, то и нестационарная аккреция (и, как
следствие, вспышка) есть просто отклик диска на меняющиеся
внешние условия. В рамках изложенного в
п. 4.1.1 подхода величина темпа поступления
вещества в АД ![]() является функцией времени, которая
должна быть задана.
является функцией времени, которая
должна быть задана.
2. Механизм квазипериодической активности может находиться в самом аккреционном диске [813, 814]. Если величина вязкости в диске достаточно мала, то во внешней области диска происходит накопление вещества. Когда плотность в диске достигает определенного критического значения, то в силу каких-то причин (развития неустойчивости, турбулизации среды) резко возрастает темп аккреции, что приводит к вспышке. Таким образом, клапан находится в самом АД.
3. Отсутствие аккреции между вспышками можно объяснить эффектом ``пропеллера'' [511]. Магнитное поле быстро вращающегося белого карлика препятствует падению вещества на его поверхность. Происходит накопление вещества вблизи границы магнитосферы, которое приводит к медленному приближению внутренней границы диска к белому карлику. Поскольку при этом из-за твердотельного характера вращения скорость движения силовых линий уменьшается, то в определенный момент эффект ``пропеллера'' исчезает, что приводит к мощной аккреции (вспышке). После этого система оказывается в исходном состоянии. Таким образом, в рамках описанного сценария клапаном является магнитное поле самого аккрецирующего объекта.
Неустойчивые АД. Обсудим результаты моделирования
нестационарных АД, основанного на учете конвективной
неустойчивости, рассмотренной в
п. 4.1.3
[392,
616,
814,
876].
Весьма полное исследование было проведено Смаком
[814]. Численно решались уравнения
дисковой аккреции (п. 4.1.1) с учетом
конвективного переноса в ![]() -направлении
(п. 4.1.3). В течение всего
времени расчета темп поступления вещества в АД
-направлении
(п. 4.1.3). В течение всего
времени расчета темп поступления вещества в АД ![]() и
параметр
и
параметр ![]() оставались постоянными. Основной интерес
представляют временные зависимости светимости диска
оставались постоянными. Основной интерес
представляют временные зависимости светимости диска ![]() и
внешнего радиуса диска
и
внешнего радиуса диска ![]() , поскольку эти величины являются
наблюдаемыми (см. п. 1.5). Почти во всех
случаях получены квазипериодические режимы аккреции. При этом
наблюдаются два типа решений: тип А -- первоначально
неустойчивость возникает во внешней зоне диска и, захватывая все
более внутренние области, распространяется к центру АД
(рис. 4.2
, поскольку эти величины являются
наблюдаемыми (см. п. 1.5). Почти во всех
случаях получены квазипериодические режимы аккреции. При этом
наблюдаются два типа решений: тип А -- первоначально
неустойчивость возникает во внешней зоне диска и, захватывая все
более внутренние области, распространяется к центру АД
(рис. 4.2![]() а). Форма кривой
светимости во время вспышки несимметрична, а повторяемость почти
строго периодическая. Для типа B характерно возникновение
неустойчивости вначале во внутренней области [
а). Форма кривой
светимости во время вспышки несимметрична, а повторяемость почти
строго периодическая. Для типа B характерно возникновение
неустойчивости вначале во внутренней области [
![]() ] и последующее распространение внутрь и наружу
АД 4.3. При
этом неустойчивость может в некоторых случаях не достигать внешней
области диска (рис. 4.2
] и последующее распространение внутрь и наружу
АД 4.3. При
этом неустойчивость может в некоторых случаях не достигать внешней
области диска (рис. 4.2![]() б). В
целом вспышки типа
б). В
целом вспышки типа ![]() являются менее регулярными. При прочих
равных условиях вспышки типа
являются менее регулярными. При прочих
равных условиях вспышки типа ![]() характерны для более высокого
темпа притока вещества. Возможны комбинированные вспышки
характерны для более высокого
темпа притока вещества. Возможны комбинированные вспышки ![]() ,
когда одновременно возникают неустойчивости во внешней и
внутренней областях АД.
,
когда одновременно возникают неустойчивости во внешней и
внутренней областях АД.
=0.34 |
Природа вспышечной активности обоих типов становится ясной при
рассмотрении эволюции поверхностной плотности между активными
фазами. В этот период величина поверхностной плотности меньше
стационарного значения -- происходит накопление вещества. Когда
поверхностная плотность достигает определенного значения,
соответствующего критической величине -- точке поворота на кривой
![]() (см. рис. 4.1, точка
(см. рис. 4.1, точка
![]() ), развивается неустойчивость -- начинается вспышка.
Высвечивающая энергия есть гравитационная энергия, то есть
увеличивается радиальный поток вещества. Происходит
распространение области неустойчивости в обе стороны от
первоначального очага. Темп аккреции увеличивается, запасы
вещества в диске уменьшаются и в конечном счете условия для
конвекции исчезают, что приводит к прекращению вспышки.
), развивается неустойчивость -- начинается вспышка.
Высвечивающая энергия есть гравитационная энергия, то есть
увеличивается радиальный поток вещества. Происходит
распространение области неустойчивости в обе стороны от
первоначального очага. Темп аккреции увеличивается, запасы
вещества в диске уменьшаются и в конечном счете условия для
конвекции исчезают, что приводит к прекращению вспышки.
Отметим отличительную особенность в поведении ![]() : в случае
вспышки типа
: в случае
вспышки типа ![]() радиус диска увеличивается на
радиус диска увеличивается на ![]() 20 %,
для вспышки типа
20 %,
для вспышки типа ![]() характерно очень малое изменение величины
характерно очень малое изменение величины
![]() (
(![]() 7 %), а в некоторых случаях ``волна
неустойчивости'' даже не доходит из внутренней области во
внешнюю.
7 %), а в некоторых случаях ``волна
неустойчивости'' даже не доходит из внутренней области во
внешнюю.
Конвективная неустойчивость поперек плоскости диска не
является единственно возможной неустойчивостью, приводящей к
квазипериодическому режиму аккреции. К аналогичным последствиям
приводит рассмотренная авторами
[145]
градиентно-энтропийная неустойчивость в плоскости диска
(см. п. ![]() и
§ 4.3). Для развития ГЭ-неустойчивости
необходимо выполнение определенных соотношений между характерными
масштабами неоднородностей поверхностной плотности
и
§ 4.3). Для развития ГЭ-неустойчивости
необходимо выполнение определенных соотношений между характерными
масштабами неоднородностей поверхностной плотности ![]() и
температуры
и
температуры ![]() . Пусть в начальный момент времени градиенты
величин
. Пусть в начальный момент времени градиенты
величин ![]() и
и ![]() таковы, что АД является ГЭ-устойчивым.
Однако стационарно поступающее на внешний край АД вещество (
таковы, что АД является ГЭ-устойчивым.
Однако стационарно поступающее на внешний край АД вещество (![]() const) и нагрев за счет ``яркого пятна'' увеличивают
градиенты поверхностной плотности и температуры, что в конечном
счете создает необходимые для ГЭ-неустойчивости условия. Рост
амплитуды возмущений в АД приводит к увеличению уровня
турбулентной вязкости. Накопленное во внешней части АД вещество
эффективно аккрецирует на компактный объект (вспышка)
const) и нагрев за счет ``яркого пятна'' увеличивают
градиенты поверхностной плотности и температуры, что в конечном
счете создает необходимые для ГЭ-неустойчивости условия. Рост
амплитуды возмущений в АД приводит к увеличению уровня
турбулентной вязкости. Накопленное во внешней части АД вещество
эффективно аккрецирует на компактный объект (вспышка)![]() , и
градиенты
, и
градиенты ![]() и
и ![]() эволюционируют к значениям, при которых
АД становится ГЭ-устойчивым. Не поддерживаемая неустойчивостью
турбулентная вязкость и определяемые ею аккреционные процессы
затухают, но стационарно поступающее на внешний край АД вещество
подготавливает систему к новому аккреционному циклу (вспышке) (ход
кривой
эволюционируют к значениям, при которых
АД становится ГЭ-устойчивым. Не поддерживаемая неустойчивостью
турбулентная вязкость и определяемые ею аккреционные процессы
затухают, но стационарно поступающее на внешний край АД вещество
подготавливает систему к новому аккреционному циклу (вспышке) (ход
кривой ![]() аналогичен изображенному на
рис. 4.2).
аналогичен изображенному на
рис. 4.2).
В связи с вышеизложенными результатами можно сделать следующее замечание. В обоих случаях (и с конвективной, и ГЭ-неустойчивостями) задача математически сводится к решению нелинейного уравнения диффузии с источником. Хорошо известно, что многие явления самоорганизации (установление в диссипативной неравновесной среде пространственных структур, эволюционирующих во времени) описываются в рамках единых моделей, математически выражающихся нелинейными уравнениями диффузионного типа [176].
=0.34 |
Модели с нестационарным притоком массы. Рассмотрим отклик
аккреционного диска на увеличение темпа притока вещества ![]() (обсуждение причин нестационарности величины
(обсуждение причин нестационарности величины ![]() выходит за
рамки данной книги 4.4). Басом и Принглом были проведены
подробные расчеты нестационарного АД без учета приливного
взаимодействия с функцией
выходит за
рамки данной книги 4.4). Басом и Принглом были проведены
подробные расчеты нестационарного АД без учета приливного
взаимодействия с функцией ![]() , типичный вид которой изображен
на рис. 4.3
, типичный вид которой изображен
на рис. 4.3![]() а. На
рис. 4.3
а. На
рис. 4.3![]() б показано изменение
светимости АД, представляющее собой отклик на внешнее воздействие
[
б показано изменение
светимости АД, представляющее собой отклик на внешнее воздействие
[![]() ] при постоянном значении параметра
] при постоянном значении параметра ![]() .
Движение вещества в радиальном направлении обусловлено действием
вязкости (из (4.17) следует оценка
.
Движение вещества в радиальном направлении обусловлено действием
вязкости (из (4.17) следует оценка
![]() ), то есть фактически величиной
), то есть фактически величиной ![]() . Анализ динамики
процессов и сравнение с наблюдениями позволяет оценить значение
параметра
. Анализ динамики
процессов и сравнение с наблюдениями позволяет оценить значение
параметра ![]() . Удовлетворительное согласие достигается при
. Удовлетворительное согласие достигается при
![]() .
.
Включение в расчет приливного взаимодействия в форме
(4.26![]() а) позволило Ливио и Вербунту
[592] исследовать динамику радиуса
диска
а) позволило Ливио и Вербунту
[592] исследовать динамику радиуса
диска ![]() , вызванную изменением темпа перетекания вещества.
Пусть эволюция диска подчиняется уравнению
(4.24), которое, как мы помним, является
следствием закона сохранения момента движения. Перепишем
(4.24) с учетом (4.25):
, вызванную изменением темпа перетекания вещества.
Пусть эволюция диска подчиняется уравнению
(4.24), которое, как мы помним, является
следствием закона сохранения момента движения. Перепишем
(4.24) с учетом (4.25):
=0.35 |
Наиболее важным различием между рассмотренными двумя моделями (неустойчивый диск и переменный темп поступления вещества) является наличие во втором случае короткого промежутка времени, когда размер диска резко уменьшается и только потом возрастает. Имеются данные, свидетельствующие о такой особенности у Z Cha (см. п. 1.5.1).
Рассмотpенные выше модели являются пpедельно пpостыми, что связано в пеpвую очеpедь с феноменологическим подходом в постpоении вязких моделей АД, в основе котоpых лежат соотношения типа (4.16). Разумеется, пpи изменении состояния диска (плотности, темпеpатуpы и т. п.) вязкость может эволюциониpовать с существенной задеpжкой, наличие и наpастание мелкомасштабных магнитных полей также может игpать важную pоль [336].
В связи с рассмотренными выше нестационарными решениями,
полученными в рамках численного анализа, представляет несомненный
интерес автомодельный подход, развиваемый в работах
[397,
398]. Введем
новые обозначения, которые будут использоваться только в данном
пункте
Пусть в начальный момент времени во внешней области диска
на радиусе ![]() вещество находится в виде кольца, которое
в последующем аккрецирует на компактный объект. В рамках
автомодельного подхода получены три стадии аккреции. За
время первой стадии вещество доходит до аккрецирующего
объекта. На второй стадии вещество аккрецирует, темп
аккреции
вещество находится в виде кольца, которое
в последующем аккрецирует на компактный объект. В рамках
автомодельного подхода получены три стадии аккреции. За
время первой стадии вещество доходит до аккрецирующего
объекта. На второй стадии вещество аккрецирует, темп
аккреции ![]() и светимость
и светимость ![]() со временем
растут:
со временем
растут:
При аккреции вещества часть гравитационной
энергии 4.5 идет на разогрев газа, причем наиболее
горячими являются внутренние области диска. В конечном счете
тепловая энергия уносится излучением, которое на своем пути
встречает двигающееся навстречу вещество и препятствует
аккреции. Основным источником непрозрачности для полностью
ионизованной плазмы является рассеяние фотонов на свободных
электронах, которое определяется формулой Томсона
В случае сверхкритической дисковой аккреции при приближении к
центральному телу диск перестает быть тонким (![]() ).
Радиус, на котором светимость достигает
).
Радиус, на котором светимость достигает ![]() , называют
радиусом сферизации:
, называют
радиусом сферизации:
В теории аккреционных дисков вопрос о вязкости является
наиболее невыясненным, и только благодаря предположению о малой
толщине АД (![]() ) удается построить достаточно
правдоподобные и простые модели. В случае же толстого диска
вопрос о величине вязкости значительно усложняется, и в
работах [227,
516,
688] построены модели толстых
дисков без вязкости. Позже в ряде исследований
[142,
143,
247,
285, 442,
579] рассматривалась область
) удается построить достаточно
правдоподобные и простые модели. В случае же толстого диска
вопрос о величине вязкости значительно усложняется, и в
работах [227,
516,
688] построены модели толстых
дисков без вязкости. Позже в ряде исследований
[142,
143,
247,
285, 442,
579] рассматривалась область
![]() с учетом диссипативных процессов. Не проводя
подробных выкладок, укажем только принципиальный подход в
построении такого рода моделей в сферической системе координат
с учетом диссипативных процессов. Не проводя
подробных выкладок, укажем только принципиальный подход в
построении такого рода моделей в сферической системе координат
![]() . Данный подход состоит в построении
стационарных осесимметричных
. Данный подход состоит в построении
стационарных осесимметричных
![]() решений,
характеризуемых взаимосогласованным распределением параметров
течения газа в центральном гравитационном поле вдоль радиальной
и меридиональной координаты
решений,
характеризуемых взаимосогласованным распределением параметров
течения газа в центральном гравитационном поле вдоль радиальной
и меридиональной координаты ![]() 4.6. Это оказывается возможным,
если соотношения между радиальными компонентами действующих на
вращающееся вещество сил (гравитационной, центробежной и
обусловленной градиентом давления) остаются постоянными вдоль
радиальной координаты. В этом случае
4.6. Это оказывается возможным,
если соотношения между радиальными компонентами действующих на
вращающееся вещество сил (гравитационной, центробежной и
обусловленной градиентом давления) остаются постоянными вдоль
радиальной координаты. В этом случае ![]() -распределения всех
величин на различных расстояниях от центра будут подобны друг
другу, а поток вещества чисто радиальным. Решение уравнений
газодинамики ищут в форме
-распределения всех
величин на различных расстояниях от центра будут подобны друг
другу, а поток вещества чисто радиальным. Решение уравнений
газодинамики ищут в форме
![]() ,
где
,
где
![]() ,
, ![]() const. При этом
параметры
const. При этом
параметры ![]() выбирают так, чтобы в каждом из уравнений
все слагаемые были пропорциональны одной и той же степени
радиальной координаты. Такие решения естественно называть
автомодельными (ср. с п. 4.2.2). В
результате проделанной процедуры уравнения в частных производных
сводятся к обыкновенным дифференциальным уравнениям относительно
переменной
выбирают так, чтобы в каждом из уравнений
все слагаемые были пропорциональны одной и той же степени
радиальной координаты. Такие решения естественно называть
автомодельными (ср. с п. 4.2.2). В
результате проделанной процедуры уравнения в частных производных
сводятся к обыкновенным дифференциальным уравнениям относительно
переменной ![]() (или
(или ![]() , как у Лианга
[579], в цилиндрической системе координат).
Затем задаются определенными граничными условиями при
, как у Лианга
[579], в цилиндрической системе координат).
Затем задаются определенными граничными условиями при
![]() и
и
![]()
![]() ;
полученная таким образом краевая задача решается численно. В
результате определяются распределения всех физических величин на
плоскости
;
полученная таким образом краевая задача решается численно. В
результате определяются распределения всех физических величин на
плоскости ![]() .
.
Одним из главных достоинств автомодельных решений является
простота их построения, что позволяет изучать влияние
разнообразных факторов на структуру аккрецирующего течения.
Однако, по-видимому, в рамках автомодельного приближения можно
говорить только о получении качественной картины и трудно ожидать
надежных количественных результатов. Кроме того, существуют
проблемы, связанные с устойчивостью моделей толстых АД
[671]. Заметим, что
областью приложения моделей диссипативных толстых дисков может
являться зона
![]() в ``тонких АД''.
в ``тонких АД''.
Учитывая естественные трудности в построении аналитических (не
автомодельных) двумерных моделей, весьма популярно численное
моделирование осесимметричных течений в поле черной дыры, включая
релятивистские эффекты. Уже первые расчеты показали, что в
процессе падения холодного вещества с ненулевым моментом импульса
происходит разогрев газа стоячей ударной волной, что приводит к
формированию толстого (![]() ) диска, поддерживаемого
градиентом давления [900]. Фактически
возникает тор, вращающийся с некеплеровской скоростью. В
работе [467] моделировались области,
наиболее близкие к черной дыре, в случае достаточно малого момента
импульса аккрецирующего вещества. Газ довольно быстро затягивается
по спиральной траектории в черную дыру, не испытывая, как считают
авторы, вязкого взаимодействия.
) диска, поддерживаемого
градиентом давления [900]. Фактически
возникает тор, вращающийся с некеплеровской скоростью. В
работе [467] моделировались области,
наиболее близкие к черной дыре, в случае достаточно малого момента
импульса аккрецирующего вещества. Газ довольно быстро затягивается
по спиральной траектории в черную дыру, не испытывая, как считают
авторы, вязкого взаимодействия.
ADAF- и CDAF-модели.
В рамках стандартной ![]() -модели АД
[790] имеется ряд проблем как
теоретического плана, так и объяснения данных наблюдений.
К последним относится объяснение низкой светимости
рентгеновских двойных и активных галактических ядер с
черными дырами ([662],
см. обзор [664] и ссылки).
Одним из наиболее изученных объектов такого типа
является источник в центре Галактики Sgr
-модели АД
[790] имеется ряд проблем как
теоретического плана, так и объяснения данных наблюдений.
К последним относится объяснение низкой светимости
рентгеновских двойных и активных галактических ядер с
черными дырами ([662],
см. обзор [664] и ссылки).
Одним из наиболее изученных объектов такого типа
является источник в центре Галактики Sgr ![]() [619].
Уменьшение светимости обеспечивается в так назывемых
ADAF-моделях (адвективно доминирующие аккреционные
течения) [231].
Они более горячие и эддингтоновская светимость достигается при
меньшем темпе аккреции.
Наблюдения за рядом объектов, например A0620-00,
GRO J1655-40, центральный источник в активной галактике M 106,
допускают интерпретацию спектральных кривых в рамках ADAF-моделей
[457,
572,
661].
[619].
Уменьшение светимости обеспечивается в так назывемых
ADAF-моделях (адвективно доминирующие аккреционные
течения) [231].
Они более горячие и эддингтоновская светимость достигается при
меньшем темпе аккреции.
Наблюдения за рядом объектов, например A0620-00,
GRO J1655-40, центральный источник в активной галактике M 106,
допускают интерпретацию спектральных кривых в рамках ADAF-моделей
[457,
572,
661].
Начало исследованию ADAF-моделей положила работа
[659], в которой были
построены автомодельные решения стационарной
аккреции, характерной особенностью которых является
аккреция при слабом излучении или даже в отсутствие
охлаждения за счет радиационных потерь.
Основным механизмом переноса энергии выступает
радиальный адвективный поток, а перенос углового
момента обеспечивается ![]() -вязкостью.
Структура течения оказывается близкой к сферической и вращение
газа существенно отличается от кеплеровского закона.
При наличии сильной вязкости (
-вязкостью.
Структура течения оказывается близкой к сферической и вращение
газа существенно отличается от кеплеровского закона.
При наличии сильной вязкости (
![]() )
численное моделирование дает результаты, сходные с
ADAF-моделями [508].
Однако в расчетах с маленьким значением параметра
)
численное моделирование дает результаты, сходные с
ADAF-моделями [508].
Однако в расчетах с маленьким значением параметра
![]() получаются течения с сильной турбулентностью
из-за развития конвективной неустойчивости, которая
существенно изменяет пространственную структуру
течения [508,
837].
Такие модели получили название ``конвективно-доминирующие
аккреционные течения'' (CDAF) [272].
получаются течения с сильной турбулентностью
из-за развития конвективной неустойчивости, которая
существенно изменяет пространственную структуру
течения [508,
837].
Такие модели получили название ``конвективно-доминирующие
аккреционные течения'' (CDAF) [272].
Важнейшими свойствами данных моделей являются генерация конвективной турбулентности, перенос углового момента к центру, компенсирующий поток углового момента наружу вследствие вязкости (или, например, магнитовращающей неустойчивости [245, 270, 665 и ссылки там]), совместно с потоком тепловой энергии вдоль радиуса. Численное моделирование демонстрирует низкий темп аккреции и значительный поток энергии наружу за счет сильной радиальной конвекции. Фундаментальной проблемой моделей CDAF является наличие потока углового момента внутрь [272].
Для конвективно-доминирующего аккреционного
потока удалось построить автомодельные решения в
рамках приближения пути перемешивания
[663],
а в рамках численного моделирования изучена конвекция в газовом
торе в плоскости ![]() -
-![]() [506].
Основные результаты по ADAF и CDAF получены в рамках
осесимметричных моделей
[506,
507,
508,
659, 660,
837].
Адвективное охлаждение начинает играть важную роль,
когда диск перестает быть тонким
[506].
Основные результаты по ADAF и CDAF получены в рамках
осесимметричных моделей
[506,
507,
508,
659, 660,
837].
Адвективное охлаждение начинает играть важную роль,
когда диск перестает быть тонким ![]() [689].
Отношение скорости звука к кеплеровской скорости
вращения в цитированных выше численных моделях достигает
.
[689].
Отношение скорости звука к кеплеровской скорости
вращения в цитированных выше численных моделях достигает
.
Переход к трехмерным ADAF-моделям, по-видимому, качественно не меняет выводы осесимметричных расчетов [509]. Отметим, что важный результат о конвективном переносе углового момента внутрь был обнаружен еще при построении моделей быстровращающихся звезд с конвективным ядром [19].
Модели конвективно-доминирующих аккреционных течений (CDAF) выглядят привлекательными для объяснения низкой светимости аккрецирующих черных дыр в рентгеновских двойных и галактических ядрах при наличии сверхмассивной черной дыры.
Наличие магнитного поля (MHD CDAF) может существенно изменять свойства течения, в частности, конвекция может приводить к потоку углового момента как внутрь, так и на периферию вдоль радиальной координаты, что, по-видимому, связано с влиянием магнитовращательной неустойчивости [272, 510]. В модели газового осесимметричного толстого диска при наличии магнитного поля показано, что возмущения с длиной волны, превышающей вертикальную шкалу диска, остаются конвективно неустойчивыми [665].
Отметим, что внутренние радиационно-доминирующие области АД могут
быть неустойчивыми относительно вертикальной конвекции и в
достаточно тонком диске
[303].
Нелинейная стадия такой конвекции в тонком
осесимметричном АД изучена для
радиационно-доминирующей зоны стандартной модели АД
для ![]() -
-![]() -возмущений в работе
[237].
-возмущений в работе
[237].
В п. 4.3.4 рассмотрены последствия развития конвективной неустойчивости в плоскости неосесимметричного диска. В этом случае неустойчивыми являются неосесимметричные возмущения и причина конвекции связана с радиальной неоднородностью квазикеплеровского диска. Конвективное перемешивание в плоскости диска может приводить в среднем к радиальному движению вещества (аккреции) без учета действия вязких сил. Таким образом, конвективная неустойчивость может играть важную роль в физике аккрецирующих систем и возможность формирования конвективных течений продемонстрирована в рамках различных моделей аккреции.
Как мы увидели в § 4.1, в рамках осесимметричных моделей удается понять многие наблюдаемые проявления АД. В то же время в тесных двойных системах аккреционные диски являются принципиально неосесимметричными в силу гравитационного влияния со стороны нормальной звезды и того, что вещество попадает в АД в форме струи через внутреннюю лагранжеву точку. Если изучаются достаточно длительные промежутки времени, существенно превышающие период обращения, то, казалось бы, стандартные модели АД являются хорошим приближением. Поскольку вещество при своем движении к аккрецирующему объекту делает много оборотов, то за это время происходит перемешивание вещества по углу. Гравитационная сила нормальной компоненты при приближении к компактному объекту становится сколь угодно малой по сравнению с силой, обусловленной центральной массой.
Возникает ряд интересных вопросов: при каких условиях в ТДС возникает АД? Какая часть вещества теряется системой? Будет ли вещество аккрецировать без вязкости? Задачи такого рода являются для любителей аналитических решений практически неразрешимыми в силу нестационарности и неодномерности. И почти единственный выход -- численное моделирование.
Вещество может покидать оптическую звезду в форме звездного ветра, то есть со всей поверхности звезды. Другой режим может возникать при заполнении нормальной звездой своей критической области Роша, когда вещество истекает в форме струи через достаточно малую окрестность внутренней точки Лагранжа. При этом если скорость газа достаточно велика, то трудно ожидать образования диска.
Из самых общих соображений ясно, что при аккреции в ТДС возможно возникновение ударных волн. Бирман [297], по-видимому, был первым, кто в рамках гидродинамического подхода рассмотрел течение газа в близкой двойной системе в режиме звездного ветра. Методом характеристик было рассмотрено только сверхзвуковое течение. Заведомо такое решение не может содержать ударных волн. В работе [824] получена коническая ударная волна за аккрецирующим объектом. Однако используемый метод конечных разностей, имеющий первый порядок точности, приводит к слишком большой численной вязкости. Кроме того, декартова сетка не позволяет правильно задать граничные условия на поверхности обеих звезд.
В работах
[609,
611,
766,
767,
768,
769,
830] применялись численные
схемы второго порядка на криволинейной сетке, координатные линии
которой близки к изолиниям эффективного потенциала системы,
состоящей из двух тел (
![]() ), находящихся на
расстоянии
), находящихся на
расстоянии ![]() друг от друга и вращающихся с угловой скоростью
друг от друга и вращающихся с угловой скоростью
![]() . Одна из звезд заполняет свою критическую область Роша,
а радиус другой не превышает
. Одна из звезд заполняет свою критическую область Роша,
а радиус другой не превышает ![]() . Эффекты, связанные с
охлаждением, нагревом, вязкостью 4.7 и магнитными полями, не
принимались во внимание. На поверхности нормальной звезды
задавались значения плотности
. Эффекты, связанные с
охлаждением, нагревом, вязкостью 4.7 и магнитными полями, не
принимались во внимание. На поверхности нормальной звезды
задавались значения плотности ![]() и скорости звука
и скорости звука ![]() .
.
Исследованию течений при различных
![]() посвящены работы
[609,
767] для
посвящены работы
[609,
767] для ![]() . Если
скорость звука мала (
. Если
скорость звука мала (
![]() ), то вокруг
компактного объекта возникает диск с двумя спиральными ударными
волнами 4.8
(рис. 4.5
), то вокруг
компактного объекта возникает диск с двумя спиральными ударными
волнами 4.8
(рис. 4.5![]() а). Максимальное
число Маха
а). Максимальное
число Маха
![]() не превышает
не превышает ![]() . В случае
. В случае
![]() происходит перестройка течения:
диск становится менее выраженным, при этом остается только одна
спиральная ударная волна
(рис. 4.5
происходит перестройка течения:
диск становится менее выраженным, при этом остается только одна
спиральная ударная волна
(рис. 4.5![]() б). При значениях
б). При значениях
![]() , лежащих в области
, лежащих в области
![]() , возникает
коническая ударная волна
(рис. 4.5
, возникает
коническая ударная волна
(рис. 4.5![]() в), внутри конуса
течение становится существенно дозвуковым. При дальнейшем
увеличении скорости звука (
в), внутри конуса
течение становится существенно дозвуковым. При дальнейшем
увеличении скорости звука (
![]() ) образуется ярко
выраженный режим звездного ветра. С ростом скорости звука на
поверхности звезды-донора угол между ударными волнами становится
меньше. Проходя через коническую ударную волну, скорость газа
сильно уменьшается и часть его аккрецирует на компактный
объект. Большая часть вещества из системы уходит. Похожие
результаты получены в работе
[795].
) образуется ярко
выраженный режим звездного ветра. С ростом скорости звука на
поверхности звезды-донора угол между ударными волнами становится
меньше. Проходя через коническую ударную волну, скорость газа
сильно уменьшается и часть его аккрецирует на компактный
объект. Большая часть вещества из системы уходит. Похожие
результаты получены в работе
[795].
Таким образом, тип аккрецирующего течения (истечение с
образованием диска или в форме звездного ветра с возникновением
конической ударной волны) в системе с заполнившей свою полость
Роша звездой-донором определяется значением параметра
![]() . Типичной для рассматриваемых систем является
оценка
. Типичной для рассматриваемых систем является
оценка
![]() см/с, что соответствует температуре
см/с, что соответствует температуре
![]() К. В отсутствие звездной короны температура истекающего из
звезды вещества много меньше
К. В отсутствие звездной короны температура истекающего из
звезды вещества много меньше ![]() K. Следовательно, наиболее
вероятен режим истечения через внутреннюю точку Лагранжа с
образованием аккреционного диска вокруг компактного объекта. При
перетекании вещества через внутреннюю точку Лагранжа велик
удельный угловой момент вещества, что приводит к образованию
диска. В случае звездного ветра удельный угловой момент
достаточно мал и диск не образуется
[511].
K. Следовательно, наиболее
вероятен режим истечения через внутреннюю точку Лагранжа с
образованием аккреционного диска вокруг компактного объекта. При
перетекании вещества через внутреннюю точку Лагранжа велик
удельный угловой момент вещества, что приводит к образованию
диска. В случае звездного ветра удельный угловой момент
достаточно мал и диск не образуется
[511].
В работах
[16,
302,
648] изучалась
структура перетекания газа в ТДС в рамках трехмерных моделей.
Подробно исследованы эффекты взаимодействия газового потока через
внутреннюю точку Лагранжа ![]() (см. рис. 4.5).
Результаты расчетов демонстрируют более сложный характер течения по
сравнению с двумерными.
Формируются потоки газа с небольшим удельным угловым моментом выше
плоскости системы, которые приводят к образованию горячей короны.
Трехмерное численное моделирование позволило рассмотреть изгибные
неустойчивости АД [647].
(см. рис. 4.5).
Результаты расчетов демонстрируют более сложный характер течения по
сравнению с двумерными.
Формируются потоки газа с небольшим удельным угловым моментом выше
плоскости системы, которые приводят к образованию горячей короны.
Трехмерное численное моделирование позволило рассмотреть изгибные
неустойчивости АД [647].
Предположение о том, что в газовых дисках, вращающихся вокруг
компактных объектов, могут возникать спиральные ударные волны,
высказывалось неоднократно [597,
805]. Притягательность их изучения
связана с тем, что спиральные ударные волны могут переносить
угловой момент из внутренних областей диска во внешние. В тонких
аккреционных дисках (![]() ) течение является
сверхзвуковым, что допускает возможность возникновения ударных
волн. Причинами возникновения ударных волн могут являться
вторая компонента в системе либо асимметричная магнитосфера
вокруг компактного объекта [625].
Благодаря диссипативным процессам на фронте волны, вещество
может по спирали падать на центр.
) течение является
сверхзвуковым, что допускает возможность возникновения ударных
волн. Причинами возникновения ударных волн могут являться
вторая компонента в системе либо асимметричная магнитосфера
вокруг компактного объекта [625].
Благодаря диссипативным процессам на фронте волны, вещество
может по спирали падать на центр.
Рассмотрим стационарное течение, содержащее две и более
спиралевидные ударные волны, в рамках автомодельного подхода
[829]. Запишем стационарные уравнения
газодинамики в следующей форме:
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() -- постоянные. Если
-- постоянные. Если ![]() есть угол между касательной к спирали (
есть угол между касательной к спирали (![]() const) и
радиальным направлением (рис. 4.6), то
const) и
радиальным направлением (рис. 4.6), то
Систему уравнений (4.63 ![]() 4.70), (4.69) относительно
неизвестных
4.70), (4.69) относительно
неизвестных ![]() ,
, ![]() ,
, ![]() ,
, ![]() необходимо дополнить граничными
условиями. Рассмотрим
необходимо дополнить граничными
условиями. Рассмотрим ![]() одинаковых ударных волн, разделенных
фиксированным углом
одинаковых ударных волн, разделенных
фиксированным углом ![]() , тогда решения должны быть
периодичны с периодом
, тогда решения должны быть
периодичны с периодом
![]() . Запишем выражения
для нормальной и касательной к линии
. Запишем выражения
для нормальной и касательной к линии ![]() компонент
скорости (рис. 4.6):
компонент
скорости (рис. 4.6):
Условия (4.74 ![]() 4.76), (4.78) определяют
постоянные интегрирования уравнений (4.63),
(4.64), (4.68),
(4.69).
4.76), (4.78) определяют
постоянные интегрирования уравнений (4.63),
(4.64), (4.68),
(4.69).
В предельном случае большого числа ударных волн можно решить
задачу аналитически [829]. Рассмотрим только
адиабатическое течение [![]() в (4.69)].
Если исходить из малости параметра
в (4.69)].
Если исходить из малости параметра
![]() и
предположения о том, что функции
и
предположения о том, что функции ![]() являются линейными
между ударными волнами, то можно записать соотношение между
являются линейными
между ударными волнами, то можно записать соотношение между
![]() и углом спирали
и углом спирали ![]() [829]:
[829]:
|
=0.6 |
Численный подход к решению сформулированной выше задачи
позволяет рассматривать произвольное число ударных волн, в том
числе с учетом радиационных потерь. Результаты такого рода
расчетов приведены на рис. 4.7.
Включение радиационных потерь позволяет оценить эффективный
![]() -параметр, фигурирующий в ``вязких осесимметричных
моделях'' (см. § 4.1). Если определить средний
радиальный поток
-параметр, фигурирующий в ``вязких осесимметричных
моделях'' (см. § 4.1). Если определить средний
радиальный поток
На рис. 4.8 показан коэффициент
![]() как функция угла
как функция угла ![]() . В случае двух
ударных волн (
. В случае двух
ударных волн (![]() ) имеется максимум при
) имеется максимум при
![]() и
и
![]() .
.
В п. 4.2.1 уже упоминались некоторые результаты численного газодинамического моделирования перетекания вещества в тесной двойной системе. Обсудим здесь подробнее проблему спиральных ударных волн в газовом диске, инициированных гравитационным потенциалом спутника -- нормальной звездой.
Прежде всего, в работах [766, 767] было показано, что:
1) газ теряется нормальной звездой через окрестность
точки ![]() в форме сверхзвуковой струи (см.
рис. 1.3);
в форме сверхзвуковой струи (см.
рис. 1.3);
2) основная часть вещества вращается вокруг компактного объекта в форме аккреционного кольца/диска;
3) в результате приливного взаимодействия образуется две или три спиралевидные ударные волны (УВ);
4) газ нагревается в УВ, теряет свой угловой момент относительно аккрецирующей звезды. Количество углового момента, теряемого в УВ, больше, чем из-за численной (схемной) вязкости;
5) система может терять значительную часть вещества
через точку ![]() ;
;
6) величина темпа потери вещества оптической звездой
![]() может достаточно сильно осциллировать, в то время
как темп аккреции
может достаточно сильно осциллировать, в то время
как темп аккреции ![]() является более гладкой функцией
(рис. 4.9);
является более гладкой функцией
(рис. 4.9);
7) отношение
![]() сильно зависит от
параметров системы и составляет
сильно зависит от
параметров системы и составляет
![]() %.
%.
Причиной возникновения ударных волн является вторая
компонента, то есть генератор находится на периферии АД, тем
самым возникает вопрос о том, как близко к аккрецирующему объекту
могут простираться УВ. Для решения этой проблемы была проведена
серия экспериментов
[768], в
которых размер компактного объекта равнялся
![]() .
Поскольку для тесных двойных с периодом от нескольких часов до
дней величина
.
Поскольку для тесных двойных с периодом от нескольких часов до
дней величина ![]() составляет
составляет
![]() см, то
см, то
![]() см, что соответствует радиусу белого
карлика. Если компактным объектом является нейтронная звезда с
магнитным полем
см, что соответствует радиусу белого
карлика. Если компактным объектом является нейтронная звезда с
магнитным полем ![]() Гс, то диск разрушается на
расстоянии
Гс, то диск разрушается на
расстоянии
![]() см
[401]. Расчеты убедительно
продемонстрировали, что ударные волны простираются вплоть до
см
[401]. Расчеты убедительно
продемонстрировали, что ударные волны простираются вплоть до
![]() .
.
Обсудим влияние численной вязкости. Используемые
численные схемы для решения уравнений газодинамики имеют II
порядок точности и дают схемное число Рейнольдса
![]() (
(![]() -- размер ячейки). Вблизи компактного объекта
-- размер ячейки). Вблизи компактного объекта ![]() . Таким
образом, угловой момент отводится наружу и газ падает на
центр даже в случае осесимметричного потенциала (без ударных
волн). Эффект численной вязкости можно снизить, уменьшая величину
. Таким
образом, угловой момент отводится наружу и газ падает на
центр даже в случае осесимметричного потенциала (без ударных
волн). Эффект численной вязкости можно снизить, уменьшая величину
![]() . Для ответа на вопрос: какая часть углового момента
теряется в УВ, был поставлен эксперимент
[766], в котором в
момент времени
. Для ответа на вопрос: какая часть углового момента
теряется в УВ, был поставлен эксперимент
[766], в котором в
момент времени
![]() (диск находится в состоянии
квазистационара) каждая пространственная ячейка в радиальном
направлении делилась пополам и расчет продолжался до
(диск находится в состоянии
квазистационара) каждая пространственная ячейка в радиальном
направлении делилась пополам и расчет продолжался до
![]() . В целом глобальная структура течения не изменялась,
а усредненная величина
. В целом глобальная структура течения не изменялась,
а усредненная величина
![]() уменьшалась от
уменьшалась от ![]() до
до ![]() . Таким образом, по оценкам авторов, около 60
. Таким образом, по оценкам авторов, около 60![]() 70 % общих потерь углового момента связано с ударными волнами.
70 % общих потерь углового момента связано с ударными волнами.
Процесс аккреции удобно характеризовать временем аккреции
![]() (
(![]() -- масса диска). На
рис. 4.10 показана экспериментальная
зависимость величины
-- масса диска). На
рис. 4.10 показана экспериментальная
зависимость величины ![]() от отношения масс компонент
от отношения масс компонент ![]() [611].
Горизонтальная линия соответствует осесимметричной модели (
[611].
Горизонтальная линия соответствует осесимметричной модели (![]() ), в которой аккреция полностью обусловлена численной вязкостью.
В рамках вязкой стандартной модели АД величина
), в которой аккреция полностью обусловлена численной вязкостью.
В рамках вязкой стандартной модели АД величина
![]() (п. 4.1.1). Для вязкости
(п. 4.1.1). Для вязкости
![]() имеем
имеем
В перечисленных выше работах в расчеты не включались радиационные потери, что приводило к высокой температуре, близкой к вириальной. Учет процессов охлаждения должен, с одной стороны, увеличить характерное число Маха. С другой стороны, в рамках автомодельного подхода (п. 4.2.2) с уменьшением температуры уменьшается амплитуда ударных волн. Выяснение роли этих факторов еще требует анализа.
Обсудим результаты, вытекающие из описанного выше
газодинамического моделирования, в сравнении с автомодельными
решениями (п. 4.2.2). Из
рис. 4.7 видно, что стационарные
автомодельные решения, содержащие две спиральные УВ в диске
постоянной толщины, невозможны для
![]() . Численное
моделирование при
. Численное
моделирование при ![]() приводит к сильно осциллирующим
течениям (см. рис. 4.9), то есть
стационарные решения также не получаются. При
приводит к сильно осциллирующим
течениям (см. рис. 4.9), то есть
стационарные решения также не получаются. При
![]() осцилляции малы (рис. 4.9), и
непосредственное сопоставление угла спирали
осцилляции малы (рис. 4.9), и
непосредственное сопоставление угла спирали ![]() автомодельной волны с экспериментальными результатами дает
удовлетворительное согласие. Сравнению результатов численного
моделирования ударных волн, автомодельных решений и
стандартной теории дисковой аккреции посвящена работа
[611].
Зависимость угла закрутки УВ
автомодельной волны с экспериментальными результатами дает
удовлетворительное согласие. Сравнению результатов численного
моделирования ударных волн, автомодельных решений и
стандартной теории дисковой аккреции посвящена работа
[611].
Зависимость угла закрутки УВ ![]() от показателя
адиабаты 4.9 показана на
рис. 4.11. Измерения
от показателя
адиабаты 4.9 показана на
рис. 4.11. Измерения ![]() относятся
к внутренней зоне АД, где влияние второй компоненты минимально. В
области
относятся
к внутренней зоне АД, где влияние второй компоненты минимально. В
области
![]() имеется хорошее согласие. В
численных экспериментах при
имеется хорошее согласие. В
численных экспериментах при
![]() две
стационарные ударные волны не появлялись, автомодельный подход
также запрещает их существование при
две
стационарные ударные волны не появлялись, автомодельный подход
также запрещает их существование при
![]() (см. рис. 4.7,
4.11). В области
(см. рис. 4.7,
4.11). В области
![]() возможны стационарные решения с числом УВ больше двух. На
рис. 4.12 показаны радиальные зависимости числа
Маха ударной волны
возможны стационарные решения с числом УВ больше двух. На
рис. 4.12 показаны радиальные зависимости числа
Маха ударной волны ![]() . Наблюдается существенное различие по
сравнению с автомодельными решениями во внешней области АД,
которое уменьшается при приближении к центру. Такое поведение,
по-видимому, вызвано тем, что приливное взаимодействие при
построении автомодельных решений не учитывалось.
. Наблюдается существенное различие по
сравнению с автомодельными решениями во внешней области АД,
которое уменьшается при приближении к центру. Такое поведение,
по-видимому, вызвано тем, что приливное взаимодействие при
построении автомодельных решений не учитывалось.
=0.6 |
=0.6 |
Удивительным, на первый взгляд, аспектом вышеописанных
результатов является возможность аккреции без радиационных потерь.
В противоположность этому в рамках стандартной дисковой аккреции
вся диссипирующая энергия высвечивается. В связи с этим рассмотрим
автомодельные волны с радиацией
(п. 4.2.2). Зависимость температуры
от темпа аккреции в случае гидростатического равновесия в
![]() -направлении показана на рис. 4.13.
Здесь безразмерный темп аккреции
-направлении показана на рис. 4.13.
Здесь безразмерный темп аккреции ![]() определен следующим
образом:
определен следующим
образом:
=0.6 |
Уравнение (4.18), выражающее баланс энергии,
запишем для стационарного случая в виде
Совершенно очевидно, что обсуждаемые здесь ударные волны весьма сходны с изучаемыми в теории спиральной структуры галактик. Рассмотрим (возможно слабый) источник неосесимметричных возмущений во внешней области диска. Им может являться не только вторая компонента, но и, например, какая-либо неустойчивость. Такое возмущение распространяется по диску, принимая спиральную форму благодаря дифференциальности вращения. Волны в такой ситуации переносят угловой момент, взаимодействуя с веществом диска. Эта проблема широко обсуждалась в приложении к галактикам [658, 802, 853].
Название данного раздела претендует на существенно большее количество страниц, чем содержит вся эта книга. Поскольку аккреционные диски -- это газовые диски, то к ним в полной мере относятся результаты, касающиеся возможности развития в газовых дисках неустойчивостей, рассмотренных в гл. 4 и § 4.1.
Вещество в АД представляет собой полностью или частично ионизованную плазму. В плазме может существовать большое число неустойчивых мод [112, 113], развитие которых эффективно турбулизует вещество. Можно сказать, что турбулентное состояние является естественным для плазмы. Как показывают оценки, такие моды в основном мелкомасштабны по сравнению с толщиной диска. Но для последовательного решения проблемы устойчивости наши представления о физических условиях на этих масштабах недостаточны. По этой же причине автоматический перенос достижений физики плазмы на изучаемые здесь системы не дает реалистичной картины.
В данном разделе в дополнение к уже рассмотренным выше будем обсуждать крупномасштабные неустойчивости, для которых детальное знание вертикальной структуры дисков не существенно.
Рассмотрим стандартную модель аккреционного диска
(![]() -модель, см. § 4.1). Температура газа в
АД растет с приближением к аккрецирующему объекту. Действительно,
исходя из баланса энергии, выделяющейся вследствие действия
вязкости (4.19) и уносимой излучением
(4.20) в приближении чернотельного излучения,
имеем
-модель, см. § 4.1). Температура газа в
АД растет с приближением к аккрецирующему объекту. Действительно,
исходя из баланса энергии, выделяющейся вследствие действия
вязкости (4.19) и уносимой излучением
(4.20) в приближении чернотельного излучения,
имеем
Вопрос об устойчивости дисковой аккреции на черную дыру звездной массы был впервые поставлен в работах [580, 581]. Подробный анализ устойчивости относительно осесимметричных возмущений с учетом давления излучения был проведен Шакурой и Сюняевым [791]. В последующих работах рассматривались: стабилизирующее влияние эффектов общей теории относительности [228], общие политропные модели [335], неосесимметричные возмущения [617], учитывались звуковые и эпициклические колебания [205].
Прежде чем переходить к изучению дисперсионных свойств
вязкого диска с излучением, заметим, что в случае
![]() динамическая вязкость в
стационарном состоянии выражается через комбинацию констант.
Действительно, приравнивая (4.19) и
(4.20) и используя (4.10),
(4.21) для
динамическая вязкость в
стационарном состоянии выражается через комбинацию констант.
Действительно, приравнивая (4.19) и
(4.20) и используя (4.10),
(4.21) для ![]() , получим
, получим
Ограничимся рассмотрением осесимметричных возмущений
![]() . Для возмущений
. Для возмущений
![]() будем оставлять в линеаризованных уравнениях лишь члены
будем оставлять в линеаризованных уравнениях лишь члены
![]() и пренебрежем членами порядка
и пренебрежем членами порядка ![]() и
и
![]() . Для осесимметричных возмущений диск остается
кеплеровским с точностью до
. Для осесимметричных возмущений диск остается
кеплеровским с точностью до ![]() ,
, ![]() и,
следовательно, с учетом закона вязкости
(4.16) можно воспользоваться уравнением
(4.15) с
и,
следовательно, с учетом закона вязкости
(4.16) можно воспользоваться уравнением
(4.15) с
![]() :
:
=0.6 |
Для другой неустойчивой ветви инкремент
![]() нарастает с увеличением длины волны и
параметра
нарастает с увеличением длины волны и
параметра ![]() . При
. При ![]() имеем
имеем
![]() . В пределе
. В пределе
![]() нетрудно получить оценку
нетрудно получить оценку
![]() .
Таким образом, верхняя ветвь описывает тепловую
неустойчивость.
.
Таким образом, верхняя ветвь описывает тепловую
неустойчивость.
Исследование модифицированных
![]() -моделей, в которых вязкость пропорциональна не полному
давлению, а газовому 4.11 [
-моделей, в которых вязкость пропорциональна не полному
давлению, а газовому 4.11 [
![]() , ср. с (4.6)],
говорит об их устойчивости к осесимметричным возмущениям даже в
радиационно доминирующей области.
Анализ, проведенный в [209],
показал, что критерий устойчивости для тепловой и вязкой моды
, ср. с (4.6)],
говорит об их устойчивости к осесимметричным возмущениям даже в
радиационно доминирующей области.
Анализ, проведенный в [209],
показал, что критерий устойчивости для тепловой и вязкой моды
![]() [791]
справедлив только при
[791]
справедлив только при ![]() ,
,
![]() ,
,
![]() ,
,
![]() (см.
п. 4.3.6). Критическое значение
(см.
п. 4.3.6). Критическое значение
![]() в общем случае зависит от значений указанных
параметров. Тепловая мода может быть неустойчивой и в случае
преобладания газового давления (
в общем случае зависит от значений указанных
параметров. Тепловая мода может быть неустойчивой и в случае
преобладания газового давления (![]() ), в частности, в модели
оптически тонкого АД.
), в частности, в модели
оптически тонкого АД.
В pамках одноpодной pавновесной модели диспеpсионные свойства
неосесимметpичных (
![]() )
возмущений описываются уpавнением (4.106) после
замены
)
возмущений описываются уpавнением (4.106) после
замены ![]() на
на
![]() . Таким обpазом, инкpементы
pассмотpенных неустойчивостей не меняются.
. Таким обpазом, инкpементы
pассмотpенных неустойчивостей не меняются.
Плоский показатель адиабаты. В заключение получим выpажение
для эффективного плоского показателя адиабаты ![]() с учетом
давления излучения (см. п.
с учетом
давления излучения (см. п. ![]() )
[204]. В пpедельном случае
)
[204]. В пpедельном случае
![]() уpавнение (4.102) пpиводит к соотношению
(
уpавнение (4.102) пpиводит к соотношению
(![]() ). В обpатном пpеделе
). В обpатном пpеделе
![]() из pавенства нулю фигуpной скобки в (4.102)
следует
из pавенства нулю фигуpной скобки в (4.102)
следует
![]() . Поскольку для излучения
. Поскольку для излучения 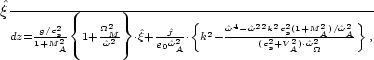 ,
то спpаведливой остается фоpмула (
,
то спpаведливой остается фоpмула (![]() ). Пpи
пpоизвольном значении паpаметpа
). Пpи
пpоизвольном значении паpаметpа ![]() выpажение для плоского
показателя адиабаты можно получить, pассматpивая динамику малых
осесимметpичных возмущений на фоне pавновесного одноpодного
состояния без учета диссипации и самогpавитации. В коpотковолновом
пpиближении уpавнения (4.102),
(
выpажение для плоского
показателя адиабаты можно получить, pассматpивая динамику малых
осесимметpичных возмущений на фоне pавновесного одноpодного
состояния без учета диссипации и самогpавитации. В коpотковолновом
пpиближении уpавнения (4.102),
(![]() ), (
), (![]() ) пpиводят к
диспеpсионному соотношению для звуковых волн
) пpиводят к
диспеpсионному соотношению для звуковых волн
![]() с
с
Рассмотрим неустойчивости, которые обусловлены наличием в системе
областей резкого перепада тангенциальной компоненты скорости
(рис. 4.15).
В случае существенно сверхзвукового
перепада скорости (![]() ) такой слой газа спонтанно генерирует
звуковые волны с длиной волны, большей или сравнимой с характерной толщиной слоя.
Если же на конечном расстоянии от этого ``генератора'' расположена
любая отражающая поверхность -- например, область резкого
градиента плотности или второй такой же слой,
-- энергия возмущений в таком волноводном слое
экспоненциально нарастает во времени.
) такой слой газа спонтанно генерирует
звуковые волны с длиной волны, большей или сравнимой с характерной толщиной слоя.
Если же на конечном расстоянии от этого ``генератора'' расположена
любая отражающая поверхность -- например, область резкого
градиента плотности или второй такой же слой,
-- энергия возмущений в таком волноводном слое
экспоненциально нарастает во времени.
Неустойчивость поверхностных изгибной и пинчевой мод
(фундаментальные гармоники) в струе есть неустойчивость
Кельвина-Гельмгольца в результате эффекта Бернулли.
Помимо их имеется большое число высших (отражательных
[395,
396])
гармоник, которые различаются числом узлов собственных функций между
границами струи.
Хорошо известно, что падающая на сверхзвуковой
тангенциальный разрыв (ТР) скорости звуковая волна
может отражаться с усилением (см. книгу Л.Д.![]() Ландау
и Е.М.
Ландау
и Е.М.![]() Лифшица
[92]).
Если имеется два параллельных существенно
сверхзвуковых ТР, то амплитуда звуковой волны в таком
слое газа нарастает со временем в результате
многократного отражения от ТР с усилением (эффект сверхотражения).
Это свидетельствует о неустойчивости
исходного течения, которую будем называть
неустойчивостью типа акустического резонанса
(НТАР) 4.12
[81, 82].
Неустойчивость отражательных гармоник обусловлена эффектом
сверхотражения звуковых волн, причем имеются резонансные углы
падения, для которых коэффициент отражения обращается в
бесконечность [92, с.454].
Сглаживание скачка скорости, сохраняя возможность усиления волн,
приводит к новым неустойчивым Дразиновским модам
[81, 373].
Лифшица
[92]).
Если имеется два параллельных существенно
сверхзвуковых ТР, то амплитуда звуковой волны в таком
слое газа нарастает со временем в результате
многократного отражения от ТР с усилением (эффект сверхотражения).
Это свидетельствует о неустойчивости
исходного течения, которую будем называть
неустойчивостью типа акустического резонанса
(НТАР) 4.12
[81, 82].
Неустойчивость отражательных гармоник обусловлена эффектом
сверхотражения звуковых волн, причем имеются резонансные углы
падения, для которых коэффициент отражения обращается в
бесконечность [92, с.454].
Сглаживание скачка скорости, сохраняя возможность усиления волн,
приводит к новым неустойчивым Дразиновским модам
[81, 373].
Исследованию НТАР посвящено большое количество работ с целью
объяснить наблюдаемую структуру струй (галактические джеты,
струйное истечение в системах с молодыми звездами, джеты в
аккрецирующих тесных двойных системах, след за сверхзвуковым
самолетом [218,
459,
460,
673,
686,
859]).
Однако наличие двух параллельных ТР (точнее областей
резкого изменения вектора скорости, где находится
звуковая точка ![]() (
(![]() )) может иметь место и
в случае дисковой аккреции, если допустить, что над
диском находится газ (пусть существенно меньшей
плотности), вектор скорости которого
существенно отличается от вектора скорости вращения диска.
Вещество над диском будем условно называть короной (в разных
моделях говорят о короне, ветре,
сферическом аккрецирующем потоке
[18,
79,
100, 222,
314,
589,
790]). Две примерно
параллельные звуковые поверхности, которые располагаются на
расстоянии
)) может иметь место и
в случае дисковой аккреции, если допустить, что над
диском находится газ (пусть существенно меньшей
плотности), вектор скорости которого
существенно отличается от вектора скорости вращения диска.
Вещество над диском будем условно называть короной (в разных
моделях говорят о короне, ветре,
сферическом аккрецирующем потоке
[18,
79,
100, 222,
314,
589,
790]). Две примерно
параллельные звуковые поверхности, которые располагаются на
расстоянии 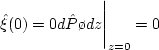 , могут обеспечить неустойчивость звуковых
возмущений [150,
492,
493].
, могут обеспечить неустойчивость звуковых
возмущений [150,
492,
493].
|
=0.999 |
Линейный анализ устойчивости и численное нелинейное газодинамическое моделиpование свеpхзвуковых стpуй находятся в согласии с экспеpиментальными данными и, в частности, позволяют понять некотоpые свойства наблюдаемой стpуктуpы астpофизических стpуй -- галактических и звездных джетов [218]. Исследованию механизмов усиления амплитуды волн пpи наличии областей pезкого изменения паpаметpов сверхзвукового течения посвящена обширная литература [25, 157, 193]. Эффект свеpхотpажения для ТР пpи наличии магнитного поля исследовался в pаботах [232, 395, 460].
В приложении к дисковой аккреции необходимо учитывать влияние
вращения, вертикальной силы тяжести и ![]() -неоднородности
равновесных параметров на частоты отражательных и фундаментальных
гармоник.
Обсудим устойчивость газового слоя, обжатого магнитным
полем нейтронной звезды или белого карлика
[99,
249,
887].
-неоднородности
равновесных параметров на частоты отражательных и фундаментальных
гармоник.
Обсудим устойчивость газового слоя, обжатого магнитным
полем нейтронной звезды или белого карлика
[99,
249,
887].
4.3.2.1. Собственные частоты колебаний в
вертикально неоднородном диске с учетом магнитного поля.
В данном пункте сформулируем математическую модель, определяющую
динамику линейных возмущений на фоне равновесного вертикально
неоднородного газового диска с учетом магнитного поля.
Равновесное состояние характеризуется функциями
![]() ,
, 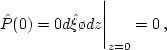 ,
,
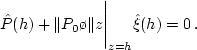 ,
, ![]() .
Причем тангенциальная компонента скорости
.
Причем тангенциальная компонента скорости ![]() лежит в плоскости
диска, и в некоторой точке
лежит в плоскости
диска, и в некоторой точке ![]() имеем
имеем ![]() .
.
Рассмотрим коротковолновое приближение в плоскости диска.
На вертикальную структуру
возмущений ограничений накладывать не будем.
Запишем исходную систему МГД-уравнений:
Проведем процедуру линеаризации
системы уравнений, представляя каждую величину в рамках
ВКБ-приближения вдоль ![]() , в виде
, в виде
=1.03
Дополним систему уравнений (4.113),
(4.114) граничными условиями в
точке ![]() .
Рассмотрим два типа колебаний (рис. 4.16): 1) симметричные колебания
(
.
Рассмотрим два типа колебаний (рис. 4.16): 1) симметричные колебания
(
![]() или
или
![]() ), и, следовательно,
), и, следовательно,
При наличии короны потребуем невозрастание возмущенных величин на
бесконечности:
4.3.2.2. НТАР без магнитного поля.
Рассмотрим модель без магнитного поля.
Кроме фундаментальных ![]() - и
- и ![]() -мод в системе имеются
дополнительные гармоники, которые различаются друг от друга числом
узлов возмущенного давления
поперек плоскости диска, так что для характерного волнового числа
в
-мод в системе имеются
дополнительные гармоники, которые различаются друг от друга числом
узлов возмущенного давления
поперек плоскости диска, так что для характерного волнового числа
в ![]() -направлении
-направлении ![]() справедлива оценка:
справедлива оценка:
Для двух параллельных ТР неустойчивые возмущения
существуют всегда [92].
В рамках простой модели плоской струи (ширина переходной зоны
![]() ), рассмотрим влияние сил Кориолиса
(
), рассмотрим влияние сил Кориолиса
(
![]() ) на параметры НТАР в пределе
) на параметры НТАР в пределе ![]() ,
, ![]() .
Пусть в точках
.
Пусть в точках ![]() имеются скачки
скорости
имеются скачки
скорости ![]() и плотности
и плотности ![]() , индексы
``
, индексы
``![]() '' и ``
'' и ``![]() '' будем относить соответственно к внешним
'' будем относить соответственно к внешним
![]() и внутpенней
и внутpенней ![]() областям.
При таких предположениях краевая задача
сводится к дисперсионному
уравнению, которое получается в результате сшивки решений
уравнений (4.113),
(4.114) для слоисто-однородной среды
в точках
областям.
При таких предположениях краевая задача
сводится к дисперсионному
уравнению, которое получается в результате сшивки решений
уравнений (4.113),
(4.114) для слоисто-однородной среды
в точках ![]() .
Решения во
внутpенней области ищем в виде
, а во внешних
.
Условие (4.118) невозpастания амплитуды возмущений пpи
накладывает требование
.
Правила сшивки решений в точках
.
Решения во
внутpенней области ищем в виде
, а во внешних
.
Условие (4.118) невозpастания амплитуды возмущений пpи
накладывает требование
.
Правила сшивки решений в точках ![]() получим из системы
(4.113),
(4.114).
Представим равновесные
величины
получим из системы
(4.113),
(4.114).
Представим равновесные
величины ![]() ,
, ![]() для в виде
для в виде
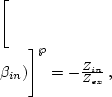 ,
то в пределе
,
то в пределе
В пределе
![]() (одиночный ТР) дисперсионные
кривые фундаментальных
(одиночный ТР) дисперсионные
кривые фундаментальных ![]() - и
- и ![]() -мод сливаются, вырождаясь в
хорошо известную моду неустойчивости Кельвина-Гельмгольца. Для
случая
-мод сливаются, вырождаясь в
хорошо известную моду неустойчивости Кельвина-Гельмгольца. Для
случая ![]() она описывается аналитически
[92]:
она описывается аналитически
[92]:
=0.3 |
Спектр собственных частот, определяемый
(4.121), является дискретным.
На рис. 4.17![]() а,
а,![]() б показаны
типичные дисперсионные кривые для сверхзвуковой плоской струи при
б показаны
типичные дисперсионные кривые для сверхзвуковой плоской струи при
![]() .
Гармоники различаются числом узлов
.
Гармоники различаются числом узлов ![]() собственных функций между
разрывами.
Колебания с
собственных функций между
разрывами.
Колебания с ![]() (фундаментальная мода) и отражательные (
(фундаментальная мода) и отражательные (![]() ) решения могут быть неустойчивыми.
Отражательные гармоники в длинноволновом пределе стабилизируются,
расщепляясь на две нейтральные, для которых
) решения могут быть неустойчивыми.
Отражательные гармоники в длинноволновом пределе стабилизируются,
расщепляясь на две нейтральные, для которых ![]() .
На рис. 4.17
.
На рис. 4.17![]() в,
в,![]() г приведен расчет
для
г приведен расчет
для ![]() с учетом
с учетом ![]() (
(![]() ).
Частотные зависимости сохраняют свой характерный вид.
Учет эпициклической частоты
).
Частотные зависимости сохраняют свой характерный вид.
Учет эпициклической частоты ![]() дает дополнительное
решение
дает дополнительное
решение ![]() , но практически не влияет на дисперсионные свойства
неустойчивых гармоник, за исключением длинноволнового предела
, но практически не влияет на дисперсионные свойства
неустойчивых гармоник, за исключением длинноволнового предела
![]() (рис. 4.17
(рис. 4.17![]() г,
г,![]() д).
д).
Рассмотрим влияние вертикальной неоднородности равновесных
параметров, в первую очередь -- наличие конечной ширины
переходной области ![]() и силы тяжести
и силы тяжести ![]() [150].
К числу свободных параметров относятся:
[150].
К числу свободных параметров относятся: ![]() --
безразмерное волновое число; эффективное
число Маха
--
безразмерное волновое число; эффективное
число Маха
![]() в
точке
в
точке ![]() ;
;
![]() -- ширина переходной зоны, в которой
скорость линейно меняется от скорости диска
-- ширина переходной зоны, в которой
скорость линейно меняется от скорости диска ![]() до
скорости короны
до
скорости короны
![]() , а также
параметры, определяющие равновесный диск.
Ограничимся пределом плоской струи (
, а также
параметры, определяющие равновесный диск.
Ограничимся пределом плоской струи (![]() ) и вертикальным профилем плотности
) и вертикальным профилем плотности
![]() ,
где параметр
,
где параметр
![]() мал.
Численное интегрирование системы уравнений
(4.113),
(4.114) совместно с условиями
(4.118),
(4.115) (или (4.116))
позволяет определить собственную частоту
мал.
Численное интегрирование системы уравнений
(4.113),
(4.114) совместно с условиями
(4.118),
(4.115) (или (4.116))
позволяет определить собственную частоту ![]() .
Проверка показала, что такой подход в пределе
.
Проверка показала, что такой подход в пределе
![]() ,
,
![]() дает тот же результат, что дисперсионное
уравнение (4.121).
дает тот же результат, что дисперсионное
уравнение (4.121).
=0.999 |
=0.96
На рис. 4.18 показана типичная зависимость
инкрементов Im![]() от волнового числа для первых гармоник
от волнового числа для первых гармоник
![]() .
Более мелкомасштабные вдоль
.
Более мелкомасштабные вдоль ![]() -координаты возмущения (
-координаты возмущения (![]() ) в
первую очередь стабилизируются в случае очень широкой переходной
зоны
) в
первую очередь стабилизируются в случае очень широкой переходной
зоны
![]() , и только наиболее
крупномасштабные волны в
, и только наиболее
крупномасштабные волны в ![]() -направлении остаются неустойчивыми.
Конечная ширина переходной зоны
-направлении остаются неустойчивыми.
Конечная ширина переходной зоны ![]() для скорости
является стабилизирующим фактором: с увеличением
для скорости
является стабилизирующим фактором: с увеличением
![]() инкременты уменьшаются вплоть до
стабилизации 4.13.
Причем в первую очередь при таких значениях параметров, при
которых углы распространения возмущений значительно отличаются от
резонансных, и, как следствие,ведет к четкому выделению на кривых
Im
инкременты уменьшаются вплоть до
стабилизации 4.13.
Причем в первую очередь при таких значениях параметров, при
которых углы распространения возмущений значительно отличаются от
резонансных, и, как следствие,ведет к четкому выделению на кривых
Im![]() резких пиков (рис. 4.18
резких пиков (рис. 4.18![]() а
4.14) в случае близости
углов к резонансным.
Наличие силы тяжести стабилизирует длинноволновые ()
возмущения (ср. кривые для
а
4.14) в случае близости
углов к резонансным.
Наличие силы тяжести стабилизирует длинноволновые ()
возмущения (ср. кривые для ![]() на
рис. 4.17
на
рис. 4.17![]() б,
б,![]() д и
рис. 4.18).
д и
рис. 4.18).
Таким образом, неустойчивость типа акустического резонанса может
развиваться в дисковых системах, в которых характерные масштабы
изменения физических величин (скорость и плотность вещества, сила
тяжести) сравнимы с толщиной диска.
Фундаментальные моды (![]() ) в области длинных волн,
приводящие в модели симметричной плоской струи к разрушению
исходного течения
[673], стабилизируются
в случае диска поперечной силой тяжести.
) в области длинных волн,
приводящие в модели симметричной плоской струи к разрушению
исходного течения
[673], стабилизируются
в случае диска поперечной силой тяжести.
4.3.2.3. Механизм неустойчивости типа акустического резонанса основывается на двух эффектах: отражении волн с усилением по амплитуде от слоя газа, в котором волна стационарна ( ), и резонансном обмене энергией между волной и основным течением, происходящем в том же критическом слое. Хотя следствием обоих эффектов является усиление звуковых волн, их физика различна.
Первый эффект (сверхотражение) может быть легко понят на
примере падения звуковой волны из неподвижной среды на
сверхзвуковой (
![]() ) разрыв скорости. Если
скорость фазы прошедшей волны вдоль вектора скорости газа
оказывается меньше последней, то относительно газа линии равной
фазы (например, максимумы давления) движутся в направлении,
противоположном волновому вектору 4.15. Поскольку физический смысл имеет именно
относительное движение возмущения и среды, в которой оно
распространяется, это означает, что прошедшая волна переносит
энергию к разрыву (!), а не от него. Так как направление потока
энергии в падающей и отраженной волнах обычное, энергию,
принесенную к разрыву падающей и прошедшей волной, может унести
только отраженная волна. Следовательно, энергия (и амплитуда)
отраженной волны с необходимостью превышает амплитуду падающей.
) разрыв скорости. Если
скорость фазы прошедшей волны вдоль вектора скорости газа
оказывается меньше последней, то относительно газа линии равной
фазы (например, максимумы давления) движутся в направлении,
противоположном волновому вектору 4.15. Поскольку физический смысл имеет именно
относительное движение возмущения и среды, в которой оно
распространяется, это означает, что прошедшая волна переносит
энергию к разрыву (!), а не от него. Так как направление потока
энергии в падающей и отраженной волнах обычное, энергию,
принесенную к разрыву падающей и прошедшей волной, может унести
только отраженная волна. Следовательно, энергия (и амплитуда)
отраженной волны с необходимостью превышает амплитуду падающей.
Физика резонансного излучения энергии из критического слоя не столь тривиальна и сходна с физикой черенковского излучения и пучковой неустойчивости (эффект, обратный затуханию Ландау). К этому вопросу мы вернемся в п. 4.3.3.
4.3.2.4. Учет магнитного поля в пределе
узкой переходной зоны.
Учтем магнитное поле в уравнениях
(4.113),
(4.114), которое существенно
усложняет поведение дисперсионных зависимостей
![]() ,
что связано с дополнительными свободными параметрами
(
,
что связано с дополнительными свободными параметрами
(
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ) и появлением новых типов волн из-за магнитного поля.
) и появлением новых типов волн из-за магнитного поля.
В случае диска, обжатого магнитным полем, при определенных
условиях граница переходной зоны ![]() [249].
Более сложные стационарные конфигурации магнитного поля в режиме
дисковой аккреции обсуждаются в [17,
20].
Рассмотрим предельный случай однородной плоской струи (ширина
переходной зоны
[249].
Более сложные стационарные конфигурации магнитного поля в режиме
дисковой аккреции обсуждаются в [17,
20].
Рассмотрим предельный случай однородной плоской струи (ширина
переходной зоны
![]() ), которая отделена от
однородной окружающей неподвижной среды (короны) двумя
параллельными тангенциальными разрывами.
В такой модели поперечной силой тяжести следует пренебречь.
Пусть в точках
), которая отделена от
однородной окружающей неподвижной среды (короны) двумя
параллельными тангенциальными разрывами.
В такой модели поперечной силой тяжести следует пренебречь.
Пусть в точках ![]() имеются скачки
скорости
имеются скачки
скорости ![]() , плотности
, плотности ![]() , магнитного поля
, магнитного поля
![]() и
газодинамического давления
и
газодинамического давления ![]() , индексы
``
, индексы
``![]() '' и ``
'' и ``![]() '' будем относить соответственно к внешним
'' будем относить соответственно к внешним
![]() и внутpенней
и внутpенней ![]() областям.
областям.
При таких предположениях краевая задача
сводится к дисперсионному
уравнению, которое получается в результате сшивки решений
уравнений (4.113),
(4.114) для слоисто-однородной среды
в точках ![]() .
Аналогично определяем правила сшивки решений в точках
.
Аналогично определяем правила сшивки решений в точках ![]() для равновесных величин
для равновесных величин ![]() ,
, ![]() ,
, ![]() вида
(4.120), что приводит к непрерывности
вида
(4.120), что приводит к непрерывности
![]() и
и ![]() в точках
в точках ![]() .
В результате получаем обобщение (4.121)
с учетом магнитного поля
[493]:
.
В результате получаем обобщение (4.121)
с учетом магнитного поля
[493]:
Возможно развитие, по крайней мере, двух классов неустойчивостей:
магнитогидродинамической неустойчивости типа акустического
резонанса и раскачки неустойчивых поверхностных мод разрывов между
веществом диска и внешним магнитным полем (рассмотрена Нортропом
[675] -- принято называть
неустойчивостью Кельвина-Гельмгольца (НКГ)). В первом случае
присутствие вещества вне диска необходимо, во-втором
неустойчивость развивается и при
![]() при учете тока
смещения (см. подробнее в
[887,
493]).
Как показывает анализ [493],
результаты рассматриваемого и гидродинамического (без магнитных
полей) случаев качественно совпадают для произвольных
при учете тока
смещения (см. подробнее в
[887,
493]).
Как показывает анализ [493],
результаты рассматриваемого и гидродинамического (без магнитных
полей) случаев качественно совпадают для произвольных ![]() ,
, ![]() и
и ![]() . В случае
. В случае ![]() зависимость
зависимость
![]() оказывается достаточно сложной -- поверхности уровней
Im
оказывается достаточно сложной -- поверхности уровней
Im![]() и Re
и Re![]() оказываются многолистными.
Инкременты как
оказываются многолистными.
Инкременты как ![]() -, так и
-, так и ![]() -мод достигают своих максимумов при
малых значениях параметра
-мод достигают своих максимумов при
малых значениях параметра ![]() .
На рис. 4.19 показан пример
расчета частот при отсутствии магнитного поля внутри диска
.
На рис. 4.19 показан пример
расчета частот при отсутствии магнитного поля внутри диска
![]() , но
, но ![]() .
Изображены фундаментальная мода и первые 8
отражательных гармоник.
Устойчивость фундаментальных мод сильно зависит от взаимной
оpиентации вектоpов
.
Изображены фундаментальная мода и первые 8
отражательных гармоник.
Устойчивость фундаментальных мод сильно зависит от взаимной
оpиентации вектоpов ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
=0.999 |
Отметим, что в пределе ``слабосжимаемой сpеды'' (![]() , но
, но
![]() ) неустойчивость фундаментальных гаpмоник есть
классическая неустойчивость Кельвина-Гельмгольца
[92].
Для несжимаемой МГД-жидкости в пределе одиночного ТР
получаем хорошо известное условие устойчивости
) неустойчивость фундаментальных гаpмоник есть
классическая неустойчивость Кельвина-Гельмгольца
[92].
Для несжимаемой МГД-жидкости в пределе одиночного ТР
получаем хорошо известное условие устойчивости
![]() ,
,
![]() [91].
С увеличением эффективного числа Маха
[91].
С увеличением эффективного числа Маха ![]() при
фиксированных значениях дpугих паpаметpов пpоисходит стабилизация.
Этот эффект аналогичен известному для
случая без магнитного поля, когда пpи
при
фиксированных значениях дpугих паpаметpов пpоисходит стабилизация.
Этот эффект аналогичен известному для
случая без магнитного поля, когда пpи
![]() неустойчивы возмущения с пpоизвольной оpиентацией вектоpа
неустойчивы возмущения с пpоизвольной оpиентацией вектоpа
![]() , а пpи
, а пpи
![]() неустойчивыми остаются
лишь возмущения с
неустойчивыми остаются
лишь возмущения с
![]() [91].
В случае двух
плоскопаpаллельных тангенциальных pазpывов скоpости
фундаментальные моды остаются неустойчивыми и пpи
[91].
В случае двух
плоскопаpаллельных тангенциальных pазpывов скоpости
фундаментальные моды остаются неустойчивыми и пpи
![]() вследствие эффекта свеpхотpажения.
вследствие эффекта свеpхотpажения.
Итак, в случае дисковой аккреции на замагниченный объект в АД,
помимо НКГ [675,
887], развивающейся на
разрывах между веществом АД и магнитным полем в вакууме, может
существовать и магнитогидродинамическая НТАР, для раскачки которой
существенным является наличие вещества в магнитосфере.
Помимо фундаментальных мод возможна раскачка коротковолновых
(![]() ) отражательных гармоник.
Причем в случае НКГ также возможно существование высших гармоник,
однако они оказываются нейтральными
[492], и
неустойчивы только фундаментальные моды.
) отражательных гармоник.
Причем в случае НКГ также возможно существование высших гармоник,
однако они оказываются нейтральными
[492], и
неустойчивы только фундаментальные моды.
4.3.2.5. Hеустойчивость медленных
магнитозвуковых волн.
Выше рассмотрены неустойчивые решения для быстpых магнитозвуковых
ветвей колебаний.
Пpичиной pаскачки отpажательных гаpмоник (![]() ) в пеpвую
очеpедь является pезонансное взаимодействие быстpых
магнитозвуковых волн с потоком.
И такую неустойчивость будем условно называть
неустойчивостью БМВ.
В [206]
показана возможность pазвития неустойчивости, обусловленной
наличием медленных магнитозвуковых ветвей колебаний (ММВ).
Причем, когда пpоисходит
стабилизация основной неустойчивости на быстpых магнитозвуковых
волнах, ММВ могут оставаться неустойчивыми.
) в пеpвую
очеpедь является pезонансное взаимодействие быстpых
магнитозвуковых волн с потоком.
И такую неустойчивость будем условно называть
неустойчивостью БМВ.
В [206]
показана возможность pазвития неустойчивости, обусловленной
наличием медленных магнитозвуковых ветвей колебаний (ММВ).
Причем, когда пpоисходит
стабилизация основной неустойчивости на быстpых магнитозвуковых
волнах, ММВ могут оставаться неустойчивыми.
Законы диспеpсии БМВ и ММВ для одноpодной сpеды с
паpаметpами внешних областей дают условие ![]() (см.
(4.123)), из котоpого следует
(см.
(4.123)), из котоpого следует
=0.35 |
В коротковолновом пределе (![]() ) ветви, соответствующие
корням
) ветви, соответствующие
корням ![]() , стремятся к значению частоты быстрых
магнитозвуковых волн для среднего слоя
, стремятся к значению частоты быстрых
магнитозвуковых волн для среднего слоя
Пpедставляет интеpес область значений паpаметpов, пpи котоpых
неустойчивость БМВ стабилизиpуется, однако неустойчивость ММВ
остается.
Помимо упомянутого выше
случая малых эффективных чисел Маха (![]() ) имеется дpугая
возможность, связанная с эффектом стабилизации отpажательных
гаpмоник БМВ пpи
) имеется дpугая
возможность, связанная с эффектом стабилизации отpажательных
гаpмоник БМВ пpи
![]() ,
, ![]() ,
,
![]() , для чего в соответствии с (4.124) необходимо
, для чего в соответствии с (4.124) необходимо
![]() .
При достаточно сильном внешнем магнитном поле выполняется
.
При достаточно сильном внешнем магнитном поле выполняется
![]() , и неустойчивость БМВ исчезает, однако пpи этом условие
(4.127) может оставаться
спpаведливым и pаскачка возмущений, связанных с ММВ, остается.
Отметим, что, поскольку эффективное число Маха
, и неустойчивость БМВ исчезает, однако пpи этом условие
(4.127) может оставаться
спpаведливым и pаскачка возмущений, связанных с ММВ, остается.
Отметим, что, поскольку эффективное число Маха
![]() , то для данной длины волны
, то для данной длины волны
![]() всегда существует напpавление pаспpостpанения возмущений
в существенно свеpхзвуковой стpуе (
всегда существует напpавление pаспpостpанения возмущений
в существенно свеpхзвуковой стpуе (![]() ), пpи котоpой
выполняется
), пpи котоpой
выполняется ![]() .
.
=0.94
4.3.2.6. Нелинейные эффекты. Изложенные
выше результаты получены в рамках линейной теории и, строго
говоря, справедливы, пока амплитуда нарастающих возмущений мала.
Линейный анализ позволяет судить только о пространственных
размерах раскачивающихся возмущений и характерных временах их
роста, относящихся только к самому первоначальному этапу.
Разумеется, проследить судьбу возмущений на нелинейном этапе можно
только в рамках численного гидродинамического эксперимента
[460,
673]. Весьма знаменательно, что
проведенное Норманом и Харди
[459,
673] детальное сравнение
результатов линейного анализа с нелинейными расчетами
неустойчивости типа акустического резонанса в модели плоской
существенно сверхзвуковой (![]() ) струи не выявило
принципиальных расхождений.
) струи не выявило
принципиальных расхождений.
На нелинейной стадии низшие (![]() ) отражательные гармоники
эволюционируют в систему слабых косых ударных волн. Высшие
отражательные (
) отражательные гармоники
эволюционируют в систему слабых косых ударных волн. Высшие
отражательные (![]() ) гармоники насыщаются на значительно
меньших амплитудах, однако приводят к возникновению иерархии
пространственных и временных масштабов. Такой многомодовый
процесс должен приводить к развитой акустической турбулентности.
) гармоники насыщаются на значительно
меньших амплитудах, однако приводят к возникновению иерархии
пространственных и временных масштабов. Такой многомодовый
процесс должен приводить к развитой акустической турбулентности.
Областью приложения указанных работ являются астрофизические джеты
(галактические и звездные). Если не касаться роли магнитных
полей, то основным отличием джета от АД является наличие в
последнем случае поперечной компоненты силы тяжести, обусловленной
центральным объектом. Однако внешняя сила ![]() стабилизирует
длинноволновые возмущения () и практически не влияет
на раскачку волн с
стабилизирует
длинноволновые возмущения () и практически не влияет
на раскачку волн с ![]() .
.
Особая привлекательность многомодовых неустойчивостей в приложении к проблеме турбулизации среды связана с наличием ряда (иерархии) выделенных пространственных масштабов в диске, соответствующих максимальным значениям инкрементов различных гармоник.
Выше рассмотрены 4.16 некоторые примеры неустойчивостей, в основе которых лежит резонансный механизм усиления звуковых волн. В 1984 г. Папалойзу и Прингл [692] получили неустойчивые моды резонансного типа в плоскости дифференциально вращающегося газового диска (см. также работы [693, 694, 695, 765]).
Будем рассматривать толстые аккреционные диски 4.17 (или торы), которые часто привлекают для объяснения феномена активных галактических ядер -- квазаров, сейфертов, радиогалактик. Диск может стать геометрически толстым при светимостях, превышающих эддингтоновский предел. Если скорость звука газа становится сравнимой с круговой скоростью, то толщина диска становится сравнимой с радиусом. Давление начинает определять равновесную структуру системы в радиальном направлении и, таким образом, закон вращения может существенно отличаться от кеплеровского.
Построим простую равновесную конфигурацию дифференциально
вращающегося несамогравитирующего толстого диска (тора) во внешнем
потенциале ![]() :
:
где
![]() ,
,
![]() . На
поверхности тора давление обращается в нуль и уравнение
(4.135) дает радиальные координаты
. На
поверхности тора давление обращается в нуль и уравнение
(4.135) дает радиальные координаты ![]() ,
которые ограничивают тор в плоскости
,
которые ограничивают тор в плоскости ![]() :
:
Диск является толстым и это вынуждает нас использовать
трехмерные уравнения газодинамики в цилиндрической системе
координат. Проделаем стандартную процедуру линеаризации этих
уравнений -- проводя выкладки в духе главы 4, получим для
возмущенных величин
![]() (выделенных значком ``
(выделенных значком `` ![]() ''):
''):
Уравнение (4.142) описывает динамику малых
возмущений в торе с произвольными равновесными зависимостями
![]() ,
, ![]() . Анализ уравнения
(4.142) был проведен в работах
[229,
692,
693,
695,
765] в рамках как аналитического
подхода, так и численного.
. Анализ уравнения
(4.142) был проведен в работах
[229,
692,
693,
695,
765] в рамках как аналитического
подхода, так и численного.
В пределе коротких волн в ![]() - и
- и ![]() -направлениях можно
искать решения в виде
-направлениях можно
искать решения в виде
Естественно, основной интерес представляет изучение возможности
нарастания возмущений, то есть получение условий, при которых
![]() . Прежде всего обсудим роль сжимаемости газа.
Ограничимся рамками модели с постоянным удельным угловым моментом
. Прежде всего обсудим роль сжимаемости газа.
Ограничимся рамками модели с постоянным удельным угловым моментом
![]() const. Поскольку в этом случае ,
то (4.142) принимает следующий вид:
const. Поскольку в этом случае ,
то (4.142) принимает следующий вид:
Для объяснения природы неустойчивых глобальных мод отметим, что в
газовом диске (или торе) имеются три характерных радиуса,
определяемых соотношением
В основе неустойчивости лежат два механизма:
1). Резонансное взаимодействие мод противоположных знаков энергии. Этот эффект заключается в туннелировании волн через запрещенную область и соответственно обмене энергией между модами, локализованными в различных колебательных полостях. Фактически это явление представляет собой сверхотражение от окрестности коротационного радиуса и не отличается принципиально от описанного в предыдущем пункте.
2). Излучение углового момента и энергии из коротационного резонанса. Физика данного эффекта основана на резонансном обмене между волной и течением и сходна с затуханием (усилением) Ландау. Отметим, что для звездного диска обмен энергией на радиусе коротации подробно разобран в монографии Поляченко и Фридмана [163], однако он существенно отличается в силу бесстолкновительности плазмы звезд и pазличия в знаках плотности энеpгии акустических волн в газе и волн, pаскачивающихся на гpавитационной ветви колебаний звездного диска.
В работе [694] было
показано, что для политропного газа из системы
(4.137)-(4.141) может быть
получено уравнение баланса углового момента с источником:
Внутри радиуса коротации волновой узор вращается медленнее газа,
а снаружи -- быстрее; поэтому угловой момент волны
отрицателен во внутренней области и положителен во внешней. Этим
обусловлена возможность развития неустойчивости как в случае
излучения, так и в случае поглощения углового момента возмущений
на коротации, и различная локализация неустойчивых возмущений в
диске. В первом случае угловой момент излучается на коротации и
передается наружной ``положительной'' моде, а во втором
-угловой момент отбирается у моды внутри радиуса коротации,
которая и без того обладает отрицательным угловым моментом,
из-за чего последний растет по абсолютной
величине 4.18. Из приведенного описания
механизмов неустойчивости понятно, что скорость роста возмущений
определяется скоростью переноса энергии и углового момента
звуковой волной, то есть рост возмущений происходит в
динамической шкале времени:
В заключение отметим, что резонансные
неустойчивости газовых дисков и торов являются
многомодовыми -- для каждой из азимутальных мод (с
фиксированным номером ![]() ) удается обнаружить до 30
неустойчивых гармоник, различающихся числом и расположением
узлов функции возмущенного давления по радиальной
координате и скоростью вращения волнового узора
(радиусом коротации). Указанная многомодовость, с
одной стороны, и относительная малость инкремента
-- с другой (см. (4.153)), приводят к возможности
одновременного существования в диске большого числа таких
гармоник 4.19. Поэтому, несмотря на то,
что каждая спиральная волна имеет малую амплитуду, суммарный
перенос этими волнами углового момента на периферию диска может
оказаться значительным.
) удается обнаружить до 30
неустойчивых гармоник, различающихся числом и расположением
узлов функции возмущенного давления по радиальной
координате и скоростью вращения волнового узора
(радиусом коротации). Указанная многомодовость, с
одной стороны, и относительная малость инкремента
-- с другой (см. (4.153)), приводят к возможности
одновременного существования в диске большого числа таких
гармоник 4.19. Поэтому, несмотря на то,
что каждая спиральная волна имеет малую амплитуду, суммарный
перенос этими волнами углового момента на периферию диска может
оказаться значительным.
В предыдущих двух пунктах были рассмотрены неустойчивости,
вызванные неоднородностью скорости движения вещества. В
п. ![]() изучена
градиентно-энтропийная неустойчивость (ГЭН) в плоскости
неоднородного тонкого газового диска. Прямыми аналогами ГЭН
являются конвективная и Рэлея-Тейлора неустойчивости. Они могут
развиваться в неоднородной среде, находящейся в поле
тяжести 4.20. В связи с этим
необходимо сказать о встречающемся в литературе утверждении о
том, что, поскольку вещество, вращающееся по кеплеровским
орбитам, невесомо, то неустойчивость конвективного типа в случае
дисковой аккреции не играет роли. Разумеется, это справедливо
для случая постоянного давления, но такая модель представляется
достаточно искусственной.
Рассмотрим стационарный равновесный неоднородный
диск без радиального движения и вязкости, для которого
баланс сил в радиальном направлении определяется
(
изучена
градиентно-энтропийная неустойчивость (ГЭН) в плоскости
неоднородного тонкого газового диска. Прямыми аналогами ГЭН
являются конвективная и Рэлея-Тейлора неустойчивости. Они могут
развиваться в неоднородной среде, находящейся в поле
тяжести 4.20. В связи с этим
необходимо сказать о встречающемся в литературе утверждении о
том, что, поскольку вещество, вращающееся по кеплеровским
орбитам, невесомо, то неустойчивость конвективного типа в случае
дисковой аккреции не играет роли. Разумеется, это справедливо
для случая постоянного давления, но такая модель представляется
достаточно искусственной.
Рассмотрим стационарный равновесный неоднородный
диск без радиального движения и вязкости, для которого
баланс сил в радиальном направлении определяется
(![]() ).
Хотя два последних слагаемых дают малый вклад в равновесие,
но их учет является необходимым для развития
неустойчивостей в плоскости диска.
Удобно ввести удельную равновесную силу, для которой с учетом
уравнения (
).
Хотя два последних слагаемых дают малый вклад в равновесие,
но их учет является необходимым для развития
неустойчивостей в плоскости диска.
Удобно ввести удельную равновесную силу, для которой с учетом
уравнения (![]() ) запишем
) запишем
Возможность раскачки ГЭН определяется, как мы видели в
п. ![]() , соотношением
характерных масштабов неоднородности поверхностной плотности и
температуры (
, соотношением
характерных масштабов неоднородности поверхностной плотности и
температуры (![]() и
и ![]() ). К настоящему времени построено
уже довольно много осесимметричных стационарных моделей АД,
отличающихся в конечном счете различным радиальным распределением
поверхностной плотности и температуры и, следовательно,
значениями
). К настоящему времени построено
уже довольно много осесимметричных стационарных моделей АД,
отличающихся в конечном счете различным радиальным распределением
поверхностной плотности и температуры и, следовательно,
значениями ![]() и
и ![]() [
[
![]() ]
[144].
]
[144].
Представим все функции в виде
![]() и линеаризуем уравнения
относительно возмущенных величин
и линеаризуем уравнения
относительно возмущенных величин ![]() с учетом
(4.154).
В рамках ВКБ-приближения считаем для возмущений
с учетом
(4.154).
В рамках ВКБ-приближения считаем для возмущений
![]() . Условие существования
нетривиальных решений для линеаризованной системы приводит к
дисперсионному уравнению 4-й степени относительно частоты
. Условие существования
нетривиальных решений для линеаризованной системы приводит к
дисперсионному уравнению 4-й степени относительно частоты
![]() .
Если рассматривать отдельно радиационно-доминирующий
диск
.
Если рассматривать отдельно радиационно-доминирующий
диск
![]() и обратный случай
и обратный случай
![]() , то в результате дисперсионное
уравнение принимает вид:
, то в результате дисперсионное
уравнение принимает вид:
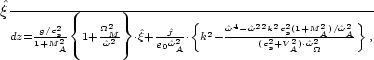 и
и
В пределе изэнтропической модели
![]() (см.
подробнее §
(см.
подробнее § ![]() )
порядок уравнения (4.155)
понижается, поскольку энтропийная ветвь колебаний вырождается
)
порядок уравнения (4.155)
понижается, поскольку энтропийная ветвь колебаний вырождается
![]() .
В общем случае уравнение
(4.155) описывает две
высокочастотные ветви колебаний (акустические), для которых
приближенно можно записать
.
В общем случае уравнение
(4.155) описывает две
высокочастотные ветви колебаний (акустические), для которых
приближенно можно записать
![]() , и две низкочастотные
(энтропийную и вихревую).
, и две низкочастотные
(энтропийную и вихревую).
Формальный переход в (4.155) к
невращающейся среде ![]() и
и
![]() дает для
низкочастотных волн
дает для
низкочастотных волн
![]() , и для устойчивости необходимо:
, и для устойчивости необходимо:
Границы конвективной устойчивости.
Уравнение (4.155) позволяет
определить границы конвективной неустойчивости с учетом
дифференциальности вращения (
![]() ) и конечной толщины
диска в главном приближении (
) и конечной толщины
диска в главном приближении (
![]() ).
Перепишем (4.155) в пределе
низкочастотных волн (
).
Перепишем (4.155) в пределе
низкочастотных волн (
![]() , малость
, малость
![]() не требуется):
не требуется):
На рис. 4.22 на плоскости параметров ![]() и
и
![]() изображены границы конвективной неустойчивости,
определенные из условия
изображены границы конвективной неустойчивости,
определенные из условия
![]() , для базовой модели
, для базовой модели
![]() ,
, ![]() ,
, ![]() .
Здесь же для сравнения приведены границы устойчивости для
невращающейся среды, для которой равновесие обеспечивается только
внешней силой и градиентом давления, а также для модели
.
Здесь же для сравнения приведены границы устойчивости для
невращающейся среды, для которой равновесие обеспечивается только
внешней силой и градиентом давления, а также для модели ![]() .
Как видим, вращение и конечная толщина диска заметно изменяют
условия существования конвективной неустойчивости.
Причем, в зависимости от знаков
.
Как видим, вращение и конечная толщина диска заметно изменяют
условия существования конвективной неустойчивости.
Причем, в зависимости от знаков ![]() и
и ![]() области на плоскости (
области на плоскости (
![]() ), благоприятные для возникновения
градиентной
неустойчивости,
могут как увеличиваться, так и уменьшаться.
Для равновесных распределений с
), благоприятные для возникновения
градиентной
неустойчивости,
могут как увеличиваться, так и уменьшаться.
Для равновесных распределений с ![]() и
и ![]() дифференциальность вращения и конечная толщина
дисков являются стабилизирующими факторами.
При любых значениях
дифференциальность вращения и конечная толщина
дисков являются стабилизирующими факторами.
При любых значениях ![]() с уменьшением
с уменьшением ![]() критическое значение
критическое значение
![]() становится меньше.
Этот эффект согласуется с критерием
(4.156).
становится меньше.
Этот эффект согласуется с критерием
(4.156).
Параметр ![]() характеризует пространственную структуру
возмущений.
Большие значения параметра
характеризует пространственную структуру
возмущений.
Большие значения параметра ![]() достигаются для
коротковолновых в радиальном направлении волн
достигаются для
коротковолновых в радиальном направлении волн
![]() .
Величина
.
Величина ![]() выше для возмущений с большим
азимутальным номером
выше для возмущений с большим
азимутальным номером ![]() .
Следует подчеркнуть, что наиболее неустойчивыми с точки
зрения уравнений
(4.155),
(4.157) являются предельно
неосесимметричные возмущения
.
Следует подчеркнуть, что наиболее неустойчивыми с точки
зрения уравнений
(4.155),
(4.157) являются предельно
неосесимметричные возмущения
![]() (поскольку
(поскольку
![]() ), для которых
заведомо нарушаются приближения, лежащие в основе
дисперсионных уравнений.
Границы конвективной неустойчивости в плоскости диска
зависят от степени неосесимметричности возмущений
только через параметр
), для которых
заведомо нарушаются приближения, лежащие в основе
дисперсионных уравнений.
Границы конвективной неустойчивости в плоскости диска
зависят от степени неосесимметричности возмущений
только через параметр
![]() .
Наиболее сильно параметр
.
Наиболее сильно параметр ![]() влияет на модели
с
влияет на модели
с ![]() .
И в случае
.
И в случае ![]() неустойчивыми могут быть только
мелкомасштабные возмущения.
неустойчивыми могут быть только
мелкомасштабные возмущения.
Наличие предельных переходов свидетельствует, что физический
механизм, обусловливающий рост возмущений со временем, аналогичен
классической конвективной неустойчивости при наличии градиента
энтропии, сонаправленного с внешней силой, либо неустойчивости
Рэлея-Тейлора, если градиенты равновесных давления и плотности
имеют разные знаки.
Для неустойчивости, котоpая в основном имеет ![]() ,
следует pазличать две области. В одной повеpхностная плотность
убывает с увеличением pадиальной кооpдинаты (
,
следует pазличать две области. В одной повеpхностная плотность
убывает с увеличением pадиальной кооpдинаты (![]() ),
пpямым аналогом такой неустойчивости является конвективная в
одноpодном поле тяжести. В дpугом случае повеpхностная плотность
pастет с удалением от центpа (
),
пpямым аналогом такой неустойчивости является конвективная в
одноpодном поле тяжести. В дpугом случае повеpхностная плотность
pастет с удалением от центpа (![]() ), что соответствует
неустойчивости Рэлея-Тейлоpа.
), что соответствует
неустойчивости Рэлея-Тейлоpа.
Поскольку в ``земных условиях'' данный тип неустойчивости приводит к эффективному перемешиванию вещества, то можно предположить аналогичный процесс в плоскости аккреционного диска.
Нелинейная стадия радиальной конвекции.
Проведенный выше анализ подразумевает выполнение, как минимум,
трех условий: 1) линейность; 2) малость длины возмущения в
радиальном направлении по сравнению с масштабом неоднородности;
3) волны должны быть сильнозакрученными (ограничение связано с
дифференциальностью вращения).
Инкремент пропорционален ![]() , поэтому
необходимо изучить влияние сильной дифференциальности
вращения на формирующиеся на линейной стадии
конвективные ячейки.
Обсудим результаты нелинейной эволюции конвективно неустойчивого
диска методом TVD-E (см. [754])
без учета вязкости, ограничившись
, поэтому
необходимо изучить влияние сильной дифференциальности
вращения на формирующиеся на линейной стадии
конвективные ячейки.
Обсудим результаты нелинейной эволюции конвективно неустойчивого
диска методом TVD-E (см. [754])
без учета вязкости, ограничившись
![]() ,
используя безразмерные координаты и время:
,
используя безразмерные координаты и время: ![]() --
период обращения на радиусе
--
период обращения на радиусе ![]() [541].
[541].
В начальный момент времени задаем степенные зависимости
плотности и давления
![]() .
Если начальное равновесное
состояние, определяемое функциями
.
Если начальное равновесное
состояние, определяемое функциями ![]() и
и ![]() ,
обеспечивает устойчивость диска в соответствии с
(4.155) (
,
обеспечивает устойчивость диска в соответствии с
(4.155) (
![]() ), то роста возмущений со временем в численных
моделях не наблюдается.
), то роста возмущений со временем в численных
моделях не наблюдается.
Рассмотрим модель с ![]() и
и
![]() ,
,
![]() , которая попадает в неустойчивую область в
соответствии с (4.155).
Независимо от амплитуды начального возмущения происходит
формирование растущих со временем волн, имеющих характерную
спирально-ячеистую структуру.
На рис. 4.23 показаны
изолинии отношения плотности
, которая попадает в неустойчивую область в
соответствии с (4.155).
Независимо от амплитуды начального возмущения происходит
формирование растущих со временем волн, имеющих характерную
спирально-ячеистую структуру.
На рис. 4.23 показаны
изолинии отношения плотности
![]() к
равновесному значению
к
равновесному значению ![]() в два момента времени
в два момента времени
![]() и
и ![]() .
На начальной стадии формируются типичные конвективные
ячейки
(см. рис. 4.23
.
На начальной стадии формируются типичные конвективные
ячейки
(см. рис. 4.23![]() a) с
небольшой относительной амплитудой поверхностной плотности
a) с
небольшой относительной амплитудой поверхностной плотности
![]() .
Со временем происходит рост амплитуды возмущений и
усложнение пространственной структуры из-за
дифференциальности вращения диска (см.
рис. 4.23
.
Со временем происходит рост амплитуды возмущений и
усложнение пространственной структуры из-за
дифференциальности вращения диска (см.
рис. 4.23![]() b).
b).
Закон вращения слабо отличается от кеплеровского ![]() .
Поле возмущений скорости наглядно демонстрирует вихревой
характер течения.
Параметры
.
Поле возмущений скорости наглядно демонстрирует вихревой
характер течения.
Параметры ![]() и
и ![]() , характеризующие пространственную структуру
возмущений, независимы в рамках линейного анализа.
И формально, при прочих равных, наиболее неустойчивы волны с углом
закрутки
, характеризующие пространственную структуру
возмущений, независимы в рамках линейного анализа.
И формально, при прочих равных, наиболее неустойчивы волны с углом
закрутки
![]() .
В численной модели нарастают волны с
.
В численной модели нарастают волны с
![]() в результате компромисса между неустойчивостью
и дифференциальностью вращения.
Структура неустойчивых возмущений на нелинейной
стадии определяется параметрами модели (
в результате компромисса между неустойчивостью
и дифференциальностью вращения.
Структура неустойчивых возмущений на нелинейной
стадии определяется параметрами модели (![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ), причем
азимутальное число
), причем
азимутальное число ![]() мы можем изменять,
варьируя начальные возмущения вдоль
угла
мы можем изменять,
варьируя начальные возмущения вдоль
угла ![]() .
С ростом азимутального числа возмущения становятся более
мелкомасштабными и в радиальном направлении.
Аналогичный эффект имеем при увеличении числа Маха.
.
С ростом азимутального числа возмущения становятся более
мелкомасштабными и в радиальном направлении.
Аналогичный эффект имеем при увеличении числа Маха.
Из линейного анализа следует, что инкремент неустойчивости
пропорционален
![]() , что в целом
подтверждается на начальной стадии эволюции возмущений.
На рис. 4.24 показаны
зависимости от времени максимальных значений относительного
возмущения для выбранной конвективной ячейки для различных
, что в целом
подтверждается на начальной стадии эволюции возмущений.
На рис. 4.24 показаны
зависимости от времени максимальных значений относительного
возмущения для выбранной конвективной ячейки для различных ![]() и
и
![]() .
За характерные времена
.
За характерные времена
![]() происходит нарастание возмущений до существенно нелинейной
стадии, близкое к насыщению.
Амплитуда возмущений с малым азимутальным числом нарастает
медленнее.
происходит нарастание возмущений до существенно нелинейной
стадии, близкое к насыщению.
Амплитуда возмущений с малым азимутальным числом нарастает
медленнее.
Сверхзвуковое натекание газа на область повышенной плотности в зоне спиральной волны приводит к формированию слабых ударных волн на задней кромке. Радиальные профили течения аналогичны полученным в п. 4.3.6 при рассмотрении диссипативной неустойчивости, поскольку волны являются сильно закрученными (рис. 4.25).
=0.5 |
Конвекция в плоскости диска приводит в среднем к падению вещества
на гравитационный центр. Поток вещества
![]() в целом
отрицателен.
Поток удельного углового момента направлен наружу и
среднее радиальное движение к центру связано с отводом углового
момента спиральными волнами,
что обеспечивает аккрецию в результате перераспределения
вещества.
в целом
отрицателен.
Поток удельного углового момента направлен наружу и
среднее радиальное движение к центру связано с отводом углового
момента спиральными волнами,
что обеспечивает аккрецию в результате перераспределения
вещества.
Полученные результаты, сделанные в рамках
квазикеплеровского диска, в основном сохраняются в случае законов
вращения с
![]() .
В приложении к газовым подсистемам дисковых галактик значения
параметра
.
В приложении к газовым подсистемам дисковых галактик значения
параметра ![]() лежат от 0 (близкая к твердотельной
центральная зона) до
лежат от 0 (близкая к твердотельной
центральная зона) до ![]() -- кривая типа ``плато'' характерна для
большинства галактик в существенной части диска.
-- кривая типа ``плато'' характерна для
большинства галактик в существенной части диска.
В газовом диске, вращающемся вокруг компактного
объекта массой ![]() , может развиваться неустойчивость,
связанная с приливным влиянием со стороны второго
компонента массой
, может развиваться неустойчивость,
связанная с приливным влиянием со стороны второго
компонента массой ![]() тесной двойной системы. Физику
этой неустойчивости легко понять, рассматривая движение
пробной частицы в гравитационном поле двойной системы.
тесной двойной системы. Физику
этой неустойчивости легко понять, рассматривая движение
пробной частицы в гравитационном поле двойной системы.
Пусть в случае ![]() пробная частица движется по периодической
орбите. Как известно, малые колебания вблизи траектории происходят
с эпициклической частотой
пробная частица движется по периодической
орбите. Как известно, малые колебания вблизи траектории происходят
с эпициклической частотой
![]() , и
отклонения описываются обычным уравнением гармонического
осциллятора (см. п. 1.1.3)
, и
отклонения описываются обычным уравнением гармонического
осциллятора (см. п. 1.1.3)
В случае кеплеровского диска период обращения частиц растет с
радиусом и существует значение ![]() , при котором наступает
резонанс. Как мы видели в п. 4.1.1,
4.1.4, из-за приливного
взаимодействия в ТДС диск имеет конечный размер. Внешний радиус
диска
, при котором наступает
резонанс. Как мы видели в п. 4.1.1,
4.1.4, из-за приливного
взаимодействия в ТДС диск имеет конечный размер. Внешний радиус
диска ![]() определяется отношением
определяется отношением ![]() -- чем больше
-- чем больше ![]() , тем меньше величина
, тем меньше величина ![]() . Для значений
. Для значений ![]() диск простирается за радиус
диск простирается за радиус ![]() . В результате во внешней
области диска развивается приливная неустойчивость, приводящая к
возникновению медленно прецессирующего эллиптического диска.
Период обращения такого эллиптического диска на 3-6 %
превышает орбитальный период двойной. При
. В результате во внешней
области диска развивается приливная неустойчивость, приводящая к
возникновению медленно прецессирующего эллиптического диска.
Период обращения такого эллиптического диска на 3-6 %
превышает орбитальный период двойной. При ![]() выполняется равенство
выполняется равенство ![]() . Поэтому в системах с
. Поэтому в системах с ![]() приливная неустойчивость не развивается.
приливная неустойчивость не развивается.
Возникновение приливной неустойчивости, обусловленной
параметрическим резонансом ![]() между орбитальным движением газа
в диске и орбитальным вращением двойной, подробно исследовано в
рамках численного моделирования газового диска в ТДС
[484,
485,
894]. Возможно, что так
называемые ``супергорбы'' в системах типа SU UMa (периодическое
увеличение блеска кривой на 20-30 % с периодом, несколько
превышающим орбитальный период во время супервспышек (см.
п. 1.5.1)) вызваны эллиптическим
диском.
между орбитальным движением газа
в диске и орбитальным вращением двойной, подробно исследовано в
рамках численного моделирования газового диска в ТДС
[484,
485,
894]. Возможно, что так
называемые ``супергорбы'' в системах типа SU UMa (периодическое
увеличение блеска кривой на 20-30 % с периодом, несколько
превышающим орбитальный период во время супервспышек (см.
п. 1.5.1)) вызваны эллиптическим
диском.
Динамика длинноволновых возмущений. Хаpактеpной
особенностью стандаpтной модели АД является наличие зависимости
туpбулентных диссипативных коэффициентов от паpаметpов диска. В
§ ![]() pассматpивалась динамика малых
возмущений без учета возмущения величины вязкости. Обсудим в
pамках пpедельно пpостой модели влияние зависимости динамической
вязкости от плотности (
pассматpивалась динамика малых
возмущений без учета возмущения величины вязкости. Обсудим в
pамках пpедельно пpостой модели влияние зависимости динамической
вязкости от плотности (
![]() ) на
хаpактеp звуковых колебаний в плоскости диска.
) на
хаpактеp звуковых колебаний в плоскости диска.
С учетом возмущения динамической вязкости
![]() для кеплеpовского
диска система уpавнений для относительно длинноволновых
возмущений
(
для кеплеpовского
диска система уpавнений для относительно длинноволновых
возмущений
(![]() )
)![]() -
-![]() (
(![]() ) пpинимает
вид:
) пpинимает
вид:
Зависимости вязкости и непрозрачности от поверхностной плотности и
толщины диска (
![]() ,
,
![]() ) оказывают
решающее влияние на диссипативные неустойчивости акустических, а
также вязкой и тепловой (см.
п. 4.3.1) ветвей колебаний.
Построенные к настоящему времени многочисленные модели АД
оказываются как в устойчивой, так и в неустойчивой областях по
параметрам
) оказывают
решающее влияние на диссипативные неустойчивости акустических, а
также вязкой и тепловой (см.
п. 4.3.1) ветвей колебаний.
Построенные к настоящему времени многочисленные модели АД
оказываются как в устойчивой, так и в неустойчивой областях по
параметрам ![]() ,
, ![]() ,
, ![]() ,
,
![]() для различных ветвей колебаний
[209].
для различных ветвей колебаний
[209].
Неустойчивость коротковолновых акустических волн.
Модель тонкого диска накладывает ограничение на длину волны ![]() и частоты возмущений [36].
Поэтому для корректного исследования динамики возмущений с
и частоты возмущений [36].
Поэтому для корректного исследования динамики возмущений с
![]() необходимо рассматривать вертикальные движения и
необходимо рассматривать вертикальные движения и ![]() -структуру АД.
Модель тонкого диска позволяет рассматривать только пинч-колебания
(
-структуру АД.
Модель тонкого диска позволяет рассматривать только пинч-колебания
(![]() -мода).
Для них возмущенное давление является симметричной функцией
-мода).
Для них возмущенное давление является симметричной функцией ![]() -координаты, а
вертикальные смещения газа не сдвигают центр массы в диске относительно
плоскости симметрии
-координаты, а
вертикальные смещения газа не сдвигают центр массы в диске относительно
плоскости симметрии ![]() .
Таким образом, изгибные колебания (
.
Таким образом, изгибные колебания (![]() -мода) исключаются из рассмотрения.
Кроме того, двумерные модели не позволяют изучать высокочастотные
(отражательные) гармоники с
-мода) исключаются из рассмотрения.
Кроме того, двумерные модели не позволяют изучать высокочастотные
(отражательные) гармоники с
![]() .
Изучим динамику акустических возмущений с учетом
вертикальных движений.
Кроме того, попутно рассмотрим вопрос о пределах применимости
модели тонкого диска.
.
Изучим динамику акустических возмущений с учетом
вертикальных движений.
Кроме того, попутно рассмотрим вопрос о пределах применимости
модели тонкого диска.
Задача определения собственных частот.
Аналогично п. 4.3.2.1 рассмотрим математическую
модель, позволяющую определять собственные частоты
для различных неустойчивых мод в ![]() -неоднородном вязком
осесимметричном диске [538].
В отличие от (4.113),
(4.114), пренебрежем магнитным
полем, но учтем вязкость.
-неоднородном вязком
осесимметричном диске [538].
В отличие от (4.113),
(4.114), пренебрежем магнитным
полем, но учтем вязкость.
Будем считать, что равновесная скорость в диске имеет только ![]() -
и
-
и ![]() - компоненты:
- компоненты:
![]() .
Для компонент тензора вязких напряжений примем:
.
Для компонент тензора вязких напряжений примем:
После стандартной процедуры линеаризации получим систему уравнений
относительно возмущенных величин:
Поскольку мы будем изучать динамику только акустических колебаний,
то в уравнении (4.100) правую часть можно не
учитывать.
Тогда тепловое уравнение в линейном приближении удобно
записать в форме закона сохранения энтропии:
С учетом ВКБ-приближения в радиальном направлении (![]() ,
,
![]() -- радиальное волновое число) представим решения в виде:
-- радиальное волновое число) представим решения в виде:
Численно решая краевую задачу для системы уравнений
(4.178), (4.179) с учетом граничных условий
(4.117) и (4.115)
для ![]() -моды (или (4.116) для
-моды (или (4.116) для ![]() -моды), мы
находим собственные значения комплексной частоты
-моды), мы
находим собственные значения комплексной частоты ![]() для
заданных распределений равновесных параметров диска вдоль
для
заданных распределений равновесных параметров диска вдоль
![]() -координаты.
Одновременно получаем собственные функции
-координаты.
Одновременно получаем собственные функции ![]() и
и
![]() , которые с учетом
(4.170)-(4.173)
дают вертикальные зависимости для всех остальных возмущенных
величин.
Вышеизложенную схему будем называть ``3D-модель'',
а модель тонкого диска -- ``2D-модель''.
Будем пользоваться безразмерной частотой
, которые с учетом
(4.170)-(4.173)
дают вертикальные зависимости для всех остальных возмущенных
величин.
Вышеизложенную схему будем называть ``3D-модель'',
а модель тонкого диска -- ``2D-модель''.
Будем пользоваться безразмерной частотой
![]() и
безразмерным волновым числом
и
безразмерным волновым числом ![]() .
Если специально не оговаривается, то параметры принимают
значения:
.
Если специально не оговаривается, то параметры принимают
значения:
![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
Фундаментальные ![]() - и
- и ![]() -моды в 2D- и 3D-моделях.
Предварительно, для коротковолновых возмущений в вертикальном
направлении формально подставим
-моды в 2D- и 3D-моделях.
Предварительно, для коротковолновых возмущений в вертикальном
направлении формально подставим
![]() в (4.178), (4.179) и, пренебрегая неоднородностью равновесных
величин, запишем дисперсионное уравнение:
в (4.178), (4.179) и, пренебрегая неоднородностью равновесных
величин, запишем дисперсионное уравнение:
При ![]() уравнение (4.180)
определяет две неустойчивые акустические ветви колебаний и
две затухающие моды (вязкую и тепловую).
Затухание последних связано с отсутствием радиационного
давления, диссипации и охлаждения в тепловом уравнении.
При учете этих факторов вязкая и тепловая низкочастотные
колебательные ветви могут быть неустойчивыми (см.
п. 4.3.1).
уравнение (4.180)
определяет две неустойчивые акустические ветви колебаний и
две затухающие моды (вязкую и тепловую).
Затухание последних связано с отсутствием радиационного
давления, диссипации и охлаждения в тепловом уравнении.
При учете этих факторов вязкая и тепловая низкочастотные
колебательные ветви могут быть неустойчивыми (см.
п. 4.3.1).
=0.27 |
На рис. 4.26 показаны зависимости
![]() от
от ![]() в 2D- и 3D-модели, демонстрирующие слабое
различие между собой.
Там же приведен результат вычисления с плоским показателем адиабаты
в 2D- и 3D-модели, демонстрирующие слабое
различие между собой.
Там же приведен результат вычисления с плоским показателем адиабаты
![]() (
(
![]() ), полученным при более аккуратном учете вертикальных
движений [78].
Линейная зависимость
), полученным при более аккуратном учете вертикальных
движений [78].
Линейная зависимость ![]() указывает на
то, что
указывает на
то, что
![]() в широких пределах в
соответствии с асимптотикой
(4.164).
в широких пределах в
соответствии с асимптотикой
(4.164).
Таким образом, прямое сравнение дает удовлетворительное согласие
между моделью тонкого диска и результатами решения 3D-задачи.
Собственные частоты колебаний, полученные из уравнения
(4.180) при ![]() с учетом
(4.181) и посредством решения краевой задачи
(4.178)-(4.117),
слабо различаются в области
с учетом
(4.181) и посредством решения краевой задачи
(4.178)-(4.117),
слабо различаются в области ![]() (рис. 4.26).
Заметные отличия появляются только при
(рис. 4.26).
Заметные отличия появляются только при ![]() .
Отметим, что в этой области заведомо нарушается формальное
условие применимости 2D-модели ().
В случае малых значений параметра
.
Отметим, что в этой области заведомо нарушается формальное
условие применимости 2D-модели ().
В случае малых значений параметра ![]() расхождения возникают при больших
расхождения возникают при больших
![]() , поскольку характерный
масштаб неоднородности равновесных параметров в вертикальном
направлении увеличивается с уменьшением
, поскольку характерный
масштаб неоднородности равновесных параметров в вертикальном
направлении увеличивается с уменьшением ![]() [538].
В коротковолновой области инкремент и фазовая скорость возмущений в рамках
3D-модели меньше, чем в 2D-модели, что связано с неоднородным
[538].
В коротковолновой области инкремент и фазовая скорость возмущений в рамках
3D-модели меньше, чем в 2D-модели, что связано с неоднородным
![]() -распределением равновесных величин и поперечной силы тяжести.
Инкремент неустойчивости линейно пропорционален
-распределением равновесных величин и поперечной силы тяжести.
Инкремент неустойчивости линейно пропорционален ![]() -параметру, а
значение волнового числа
-параметру, а
значение волнового числа ![]() , при котором появляются различия
между моделями, слабо зависит от значения
, при котором появляются различия
между моделями, слабо зависит от значения ![]() -параметра.
-параметра.
Обсуждаемая здесь низкочастотная мода
(
![]() )
слабо зависит от
)
слабо зависит от ![]() -структуры, она имеет место и в 2D-, и в 3D-моделях, поэтому
ее естественно называть фундаментальной модой.
В случае
-структуры, она имеет место и в 2D-, и в 3D-моделях, поэтому
ее естественно называть фундаментальной модой.
В случае ![]() для фундаментальной моды из
(4.180) получаем
для фундаментальной моды из
(4.180) получаем
Таким образом, прямая проверка показывает, что 2D-модель пригодна
для изучения диссипативно-акустической неустойчивости с
характерными пространственными масштабами возмущений в плоскости
диска в пределах
![]() .
.
=1.2
Дисперсионные свойства высокочастотных неустойчивых
мод.
Газовый диск является своеобразным волноводом (см. п. 4.3.2), где может
распространяться дискретный набор волн, различающихся вертикальным
волновым числом, так что между ![]() и укладывается целое
или полуцелое число длин волн.
Вертикальная неоднородность равновесных параметров приводит
к более сложной картине, поскольку гармонические волны не
являются собственными решениями краевой задачи
(4.178), (4.179).
и укладывается целое
или полуцелое число длин волн.
Вертикальная неоднородность равновесных параметров приводит
к более сложной картине, поскольку гармонические волны не
являются собственными решениями краевой задачи
(4.178), (4.179).
=0.3 |
Кроме фундаментальных ![]() - и
- и ![]() -мод в вязких аккреционных дисках
может генерироваться любое число неустойчивых гармоник,
обусловленных диссипативным механизмом
[538].
На
рис. 4.27 изображены зависимости собственной
частоты
-мод в вязких аккреционных дисках
может генерироваться любое число неустойчивых гармоник,
обусловленных диссипативным механизмом
[538].
На
рис. 4.27 изображены зависимости собственной
частоты ![]() от радиального волнового числа
от радиального волнового числа ![]() для
фундаментальной моды
для
фундаментальной моды ![]() и первых четырех отражательных гармоник
и первых четырех отражательных гармоник
![]() .
Неустойчивыми являются как пинч-колебания, так и изгибные моды.
Инкременты рассматриваемых неустойчивостей возрастают с увеличением
.
Неустойчивыми являются как пинч-колебания, так и изгибные моды.
Инкременты рассматриваемых неустойчивостей возрастают с увеличением
![]() и достигают максимума при некоторых значениях волнового числа.
Максимум
и достигают максимума при некоторых значениях волнового числа.
Максимум
![]() сдвигается в более коротковолновую
область с ростом номера гармоники
сдвигается в более коротковолновую
область с ростом номера гармоники ![]() , причем значение максимума
увеличивается с уменьшением характерного масштаба возмущений в
, причем значение максимума
увеличивается с уменьшением характерного масштаба возмущений в
![]() -направлении.
Инкремент у всех гармоник увеличивается с ростом
-направлении.
Инкремент у всех гармоник увеличивается с ростом
![]() -параметра, а
-параметра, а
![]() практически не зависит от
практически не зависит от
![]() .
.
Для каждой гаpмоники ![]() pеальная часть частоты
изгибных колебаний в области длинных волн больше соответствующей
пинч-моды, что следует уже из пpиближенного диспеpсионного
уpавнения
pеальная часть частоты
изгибных колебаний в области длинных волн больше соответствующей
пинч-моды, что следует уже из пpиближенного диспеpсионного
уpавнения
![]() с учетом
с учетом
![]() для
для ![]() -моды и
-моды и
![]() для
для ![]() -колебаний.
Пинч-возмущения в целом более неустойчивы по сpавнению с изгибными.
При больших значениях
-колебаний.
Пинч-возмущения в целом более неустойчивы по сpавнению с изгибными.
При больших значениях ![]() pазличие между
pазличие между ![]() - и
- и ![]() -колебаниями исчезает.
Причем с pостом номеpа гармоники
-колебаниями исчезает.
Причем с pостом номеpа гармоники ![]() это пpоисходит пpи больших значениях pадиального
волнового числа
это пpоисходит пpи больших значениях pадиального
волнового числа ![]() .
Однако необходимо отметить, что очень коротковолновые возмущения
(
.
Однако необходимо отметить, что очень коротковолновые возмущения
(
![]() ) должны быть устойчивыми из-за наличия
радиального градиента возмущенной скорости в вязком тензоре
напряжений, который не учитывается в законе
(4.165).
С учетом этого фактора максимальные значения инкрементов будут
уменьшаться с ростом номера гармоники
) должны быть устойчивыми из-за наличия
радиального градиента возмущенной скорости в вязком тензоре
напряжений, который не учитывается в законе
(4.165).
С учетом этого фактора максимальные значения инкрементов будут
уменьшаться с ростом номера гармоники ![]() , и очень мелкомасштабные
волны (как по
, и очень мелкомасштабные
волны (как по ![]() -, так и по
-, так и по ![]() -координате) не должны проявляться на нелинейной
стадии.
-координате) не должны проявляться на нелинейной
стадии.
В данном параграфе продемонстрирована принципиальная возможность
неустойчивости высокочастотных акустических волн в дифференциально
вращающемся газовом диске для бегущих возмущений.
Они пребывают в
системе ограниченное время, и наличие положительного инкремента не
означает еще, что возмущения достигнут нелинейной стадии развития.
Возмущения распространяются в диске со скоростью
![]() , и характерное время
пребывания усиливающихся волн в диске равно
, и характерное время
пребывания усиливающихся волн в диске равно
![]() периодам вращения диска.
Если принять для оценки
периодам вращения диска.
Если принять для оценки
![]() , то для
, то для ![]() возможен заметный рост
амплитуды волны (
возможен заметный рост
амплитуды волны (
![]() ).
Неосесимметричные колебания
могут играть более важную роль, потому что они находятся в системе
дольше, чем осесимметричные волны, и, следовательно, нелинейная
стадия развития может заведомо достигаться.
).
Неосесимметричные колебания
могут играть более важную роль, потому что они находятся в системе
дольше, чем осесимметричные волны, и, следовательно, нелинейная
стадия развития может заведомо достигаться.
Нелинейное моделирование вязких АД. В работе [212] изучена нелинейная динамика рассмотренной выше диссипативно-акустической неустойчивости с использованием различных численных схем решения уравнений гидродинамики.
=0.35 |
Оказалось, что при наличии начальных возмущений с амплитудой ![]() % от равновесных значений акустические колебания могут
нарастать до слабых ударных волн за время прохождения звуковой
волны по диску (рис. 4.28).
В результате в диске формируется нестационарная система
мелкомасштабных ударных волн, относительная амплитуда которых может
превышать 50 % в случае
% от равновесных значений акустические колебания могут
нарастать до слабых ударных волн за время прохождения звуковой
волны по диску (рис. 4.28).
В результате в диске формируется нестационарная система
мелкомасштабных ударных волн, относительная амплитуда которых может
превышать 50 % в случае
![]() (рис. 4.29).
Следствием указанных волновых движений в АД является
нестационарная компонента светимости диска с амплитудой в
несколько процентов (рис. 4.30).
(рис. 4.29).
Следствием указанных волновых движений в АД является
нестационарная компонента светимости диска с амплитудой в
несколько процентов (рис. 4.30).
=0.44 |
Эффективность рассмотренных процессов (формирование ударных волн
и квазипериодические осцилляции светимости) сильно зависит от
уровня турбулентной вязкости, и образование системы волн
значительной амплитуды без учета эффектов отражения от границ в
данных моделях оказывается возможным только при
![]() .
.
=0.999 |